【Python零基础快速入门系列 | 08】无序、不重复、元素只读，Python数据容器之集合

原创已于 2022-09-26 01:09:06 修改 · 920 阅读

5 ·

CC 4.0 BY-SA版权

文章标签：

#python #开发语言 #Python零基础 #Python笔记

于 2022-06-01 07:30:00 首次发布

Python零基础快速入门系列专栏收录该内容

16 篇文章

订阅专栏

本文介绍了Python集合的基本概念，包括集合的定义、set()函数、花括号表示法、特性（互异性、无序性），以及常用的添加、删除、修改和读取方法。还讲解了集合的运算如交集、并集、差集和对称差集，以及集合推导式的使用。适合零基础学习者快速掌握集合基础。

这是机器未来的第12篇原创文章

原文首发链接：https://blog.youkuaiyun.com/RobotFutures/article/details/125039175

在这里插入图片描述

《Python零基础快速入门系列》快速导航：

1. 集合概述

集合（set）是一个无序的不重复元素序列。集合是可变数据类型，但是其元素是不可变数据类型。它是一种存储数据的容器。

2. 集合的定义

集合的定义可以通过set()函数和花括号{}来定义。

2.1 set()函数

首先看一下set函数的定义

从上图中可以看到set函数可以支持参数为空或参数为可迭代对象

参数为空时, 定义空集合

x = set()
print(x, type(x))

参数为可迭代对象时

x = set([1, 2, 3, 4, -7])       # 输入参数为列表
print(x, type(x))

x = set((1, 2, 3, 4, -7))       # 输入参数为元组
print(x, type(x))

x = set({1:25, 2:36, 3:-9, 4:20, -7:89})    # 输入参数为字典：仅取字典的key
print(x, type(x))

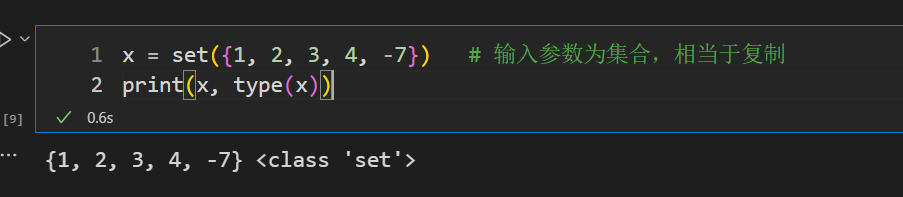
x = set({1, 2, 3, 4, -7})   # 输入参数为集合，相当于复制
print(x, type(x))

x1 = {1, 2, 3, 4, -7}
x2 = set(x1)   # 输入参数为集合，相当于复制-深拷贝
x3 = x1
print(x1, type(x1), id(x1), x2, type(x2), id(x2), x3, type(x3), id(x3))

2.2 花括号{}

定义空集合只能使用set()函数，因为{}也是字典的符号，数据为空的{}表示空字典。

x = {}
print(x, type(x))

可以看到，type(x)返回的数据类型为dict字典

含有数据集的集合定义

x = {-1, 3+6j, 'ahc', 1e-5}
print(x, type(x))

2.3 集合的特性

确定性

集合中的元素是不可变数据类型，例如数值类型、字符串类型、元组类型，而列表、字典、集合不可以是集合的元素, 它们都是可变数据类型。

x = {[1, 2, 3, 4], 5, 3+6j, 1e12, 'ahdhss'}

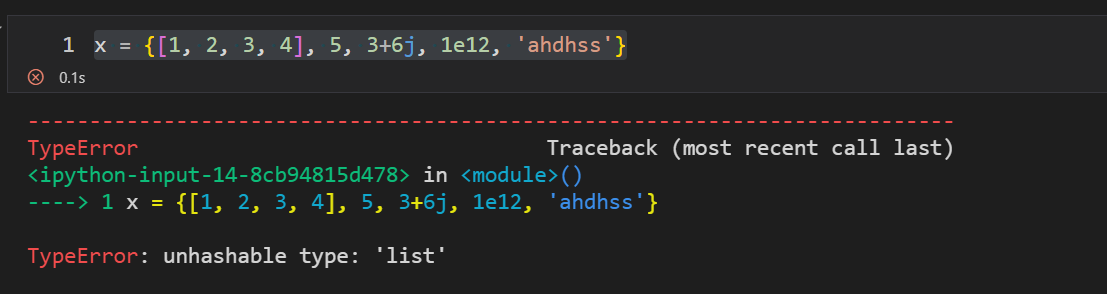
x = {{1:66, 2:77, 3:88, 4:99}, 5, 3+6j, 1e12, 'ahdhss'}

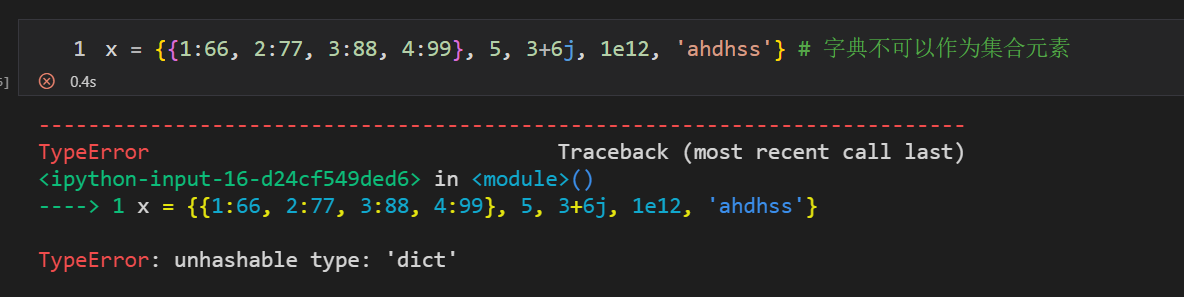
# 集合是可变数据类型，但是集合中的元素是不可变数据类型，集合中的元素是可以更改的
x = {{1, 2, 3, 4}, 5, 3+6j, 1e12, 'ahdhss'}

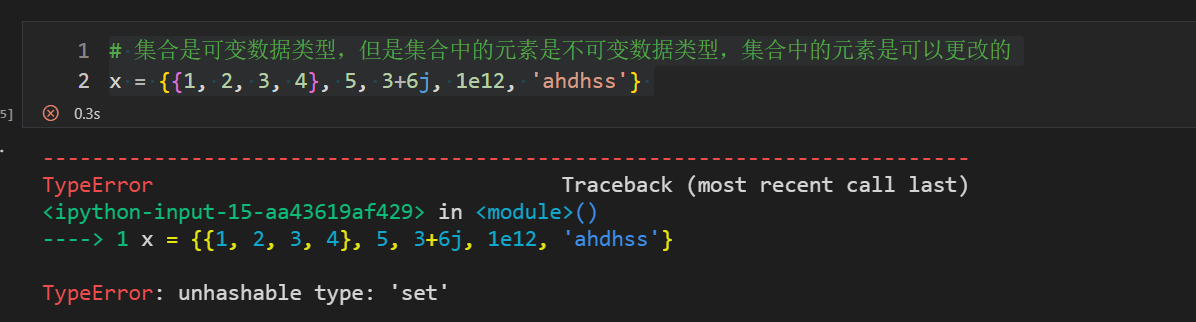
特别注意：集合是可变数据类型，但是集合中的元素是不可变数据类型，集合中的元素是可以更改的

x = {(1, 2, 3, 4), 5, 3+6j, 1e12, 'ahdhss'}
print(x, type(x))

互异性

集合中的元素是不可重复的，如果添加的值已存在于集合中，则不会添加。

x = {4, 1, 3, 4, 1, 2}
x

从上图中可以看到，集合定义时存在的两个4和两个1，均只保留一个，且集合元素始终从小到大排列。

根据集合的互斥性，可以用来处理列表或元组去重处理。

xl = [4, 1, 3, 4, 1, 2]
xs = set(xl)
xl = list(xs)
xl

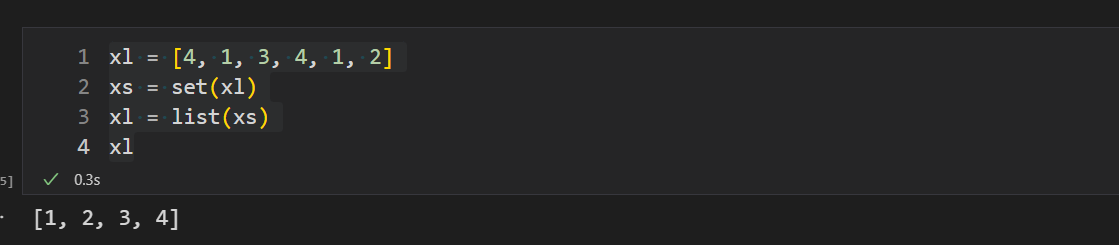
无序性

集合中的元素是无序的，无法通过索引访问，只能通过遍历的方式访问。

x = {4, 1, 3, 4, 1, 2}
x[0]

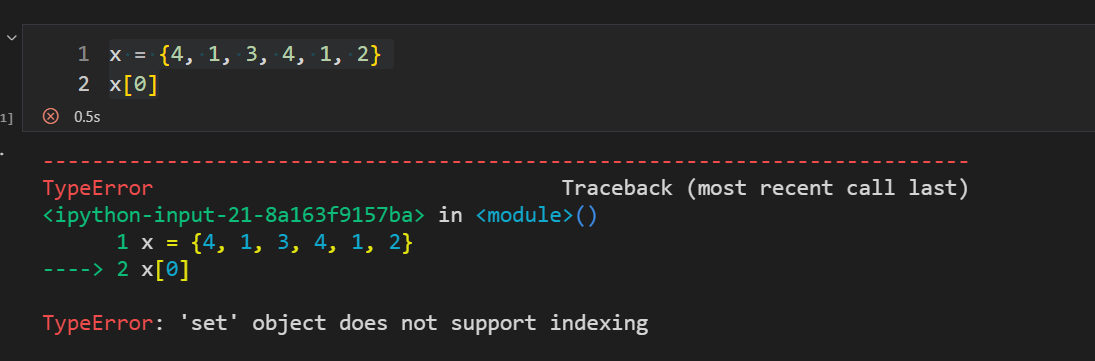
x = {4, 1, 3, 4, 1, 2}
for i in x:
    print(i, end=', ')

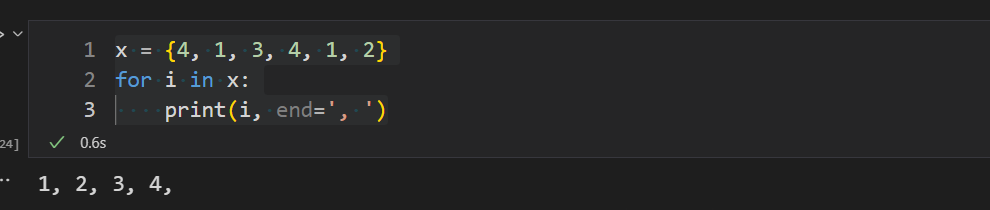
3. 集合的常用用法

x = {4, 1, 3, 4, 1, 2}
dir(x)

输出如下：

['__and__',
 '__class__',
 '__contains__',
 '__delattr__',
 '__dir__',
 '__doc__',
 '__eq__',
 '__format__',
 '__ge__',
 '__getattribute__',
 '__gt__',
 '__hash__',
 '__iand__',
 '__init__',
 '__init_subclass__',
 '__ior__',
 '__isub__',
 '__iter__',
 '__ixor__',
 '__le__',
 '__len__',
 '__lt__',
 '__ne__',
 '__new__',
 '__or__',
 '__rand__',
 '__reduce__',
 '__reduce_ex__',
 '__repr__',
 '__ror__',
 '__rsub__',
 '__rxor__',
 '__setattr__',
 '__sizeof__',
 '__str__',
 '__sub__',
 '__subclasshook__',
 '__xor__',
 'add',
 'clear',
 'copy',
 'difference',
 'difference_update',
 'discard',
 'intersection',
 'intersection_update',
 'isdisjoint',
 'issubset',
 'issuperset',
 'pop',
 'remove',
 'symmetric_difference',
 'symmetric_difference_update',
 'union',
 'update']

3.1 添加

集合使用add函数添加元素，注意事项：如果添加的元素在集合中已存在，则不会添加

x = {1, 4, 7}   
x.add(3+9j)     # 添加一个复数到集合中
x

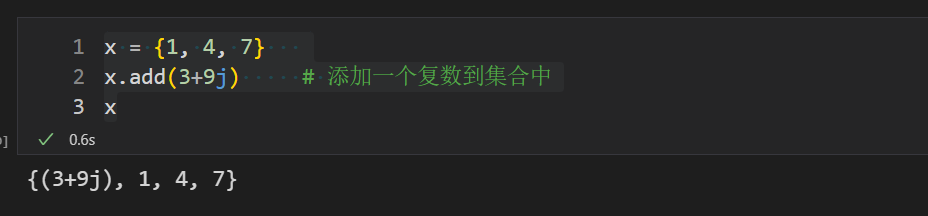
x.add(1)        # 如果添加的元素在集合中已存在，则不会添加
x

3.2 删除

删除元素的方法有4种，pop()、remove()、discard()和clear()

pop()函数

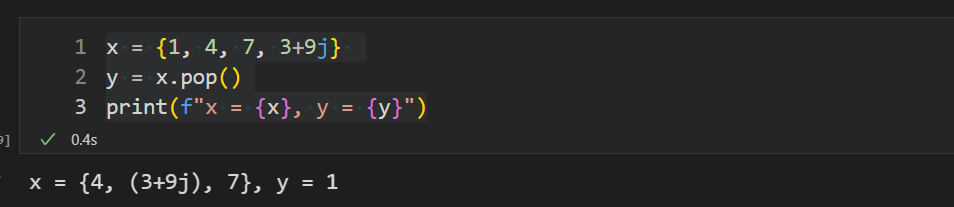
pop()函数可以随机从集合中取出一个元素，取出后该元素将不在集合中。

x = {1, 4, 7, 3+9j} 
y = x.pop()
print(f"x = {x}, y = {y}")

remove()函数

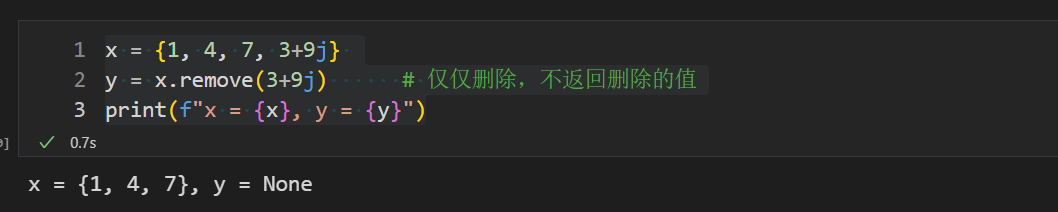
remove()函数可以指定元素从集合中删除，如果元素不存在则会报错

x = {1, 4, 7, 3+9j} 
y = x.remove(3+9j)      # 仅仅删除，不返回删除的值
print(f"x = {x}, y = {y}")

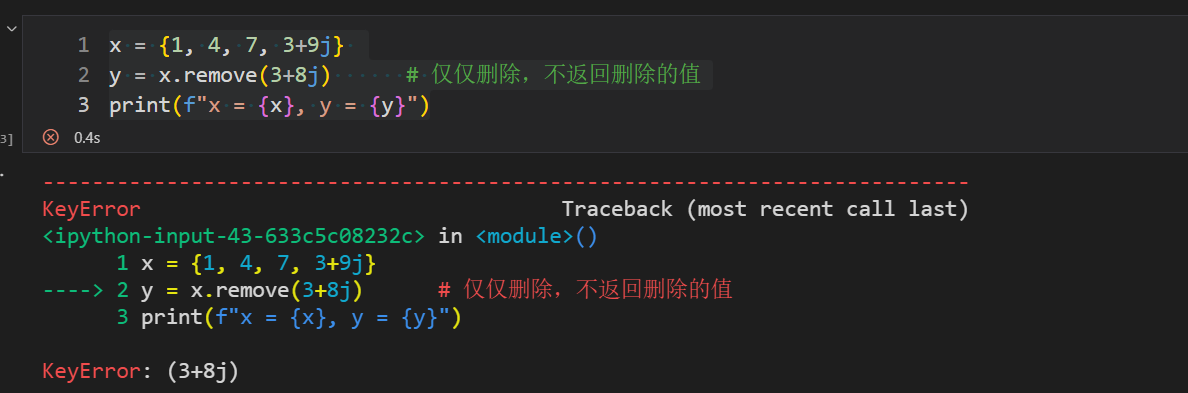
元素不存在的场景：

x = {1, 4, 7, 3+9j} 
y = x.remove(3+8j)      # 仅仅删除，不返回删除的值
print(f"x = {x}, y = {y}")

discard()删除指定元素-不存在不报错

x = {1, 4, 7, 3+9j} 
y = x.discard(3+8j)      # 不存在不报错
print(f"x = {x}, y = {y}")

clear()清除集合

x = {1, 4, 7, 3+9j} 
x.clear()
x

3.3 修改

集合不可以使用索引访问，因此如果需要修改，则执行先remove，再add

3.4 读取

x = {4, 1, 3, 4, 1, 2}
for i in x:
    print(i, end=', ')

3.5 集合运算

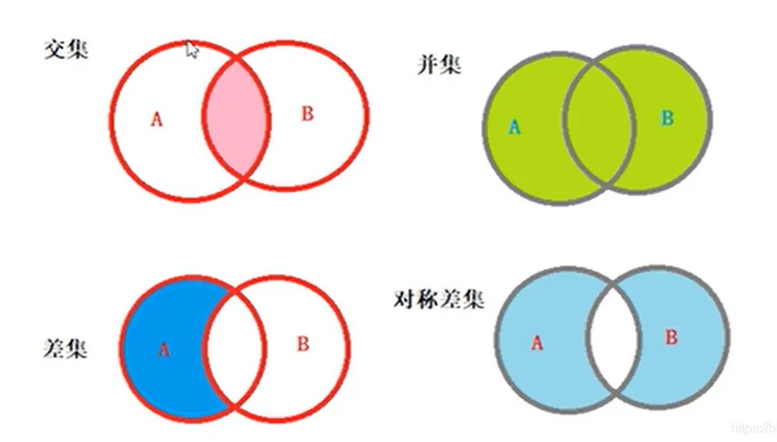
交集

两个集合共同存在的部分，即为交集。

x1 = {1, 2, 4, 7}
x2 = {4, 7, 9, 11}
x = x1.intersection(x2)
x

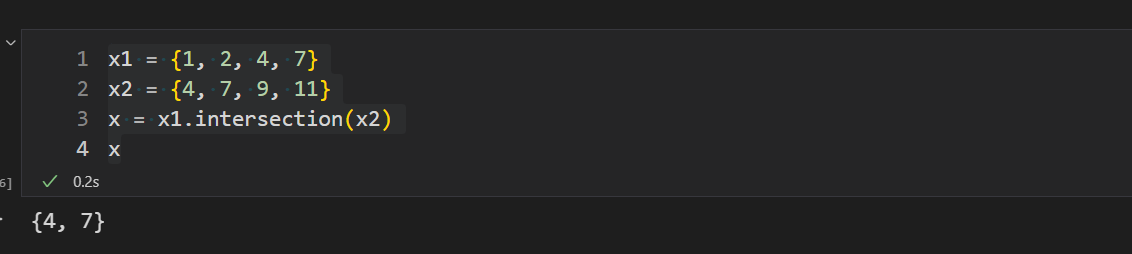
集合x1和集合x2共有的元素是4，7，因此交集为{4, 7}。

使用交集运算符&，也可以达成同样的结果

x1 = {1, 2, 4, 7}
x2 = {4, 7, 9, 11}
x = x1 & x2
x

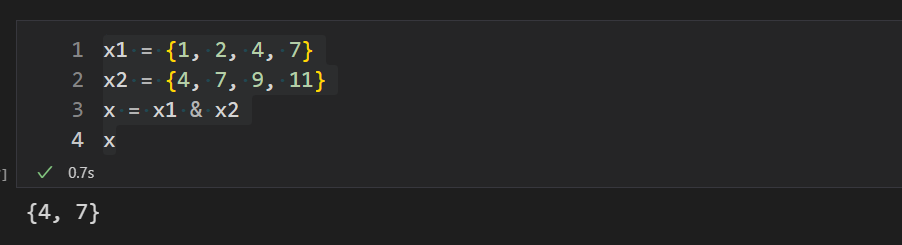
并集

两个集合的并集就是两个集合中所有的元素组合在一起形成的新的集合，即为并集。

x1 = {1, 2, 4, 7}
x2 = {4, 7, 9, 11}
x = x1.union(x2)
x

或

x1 = {1, 2, 4, 7}
x2 = {4, 7, 9, 11}
x = x1 | x2
x

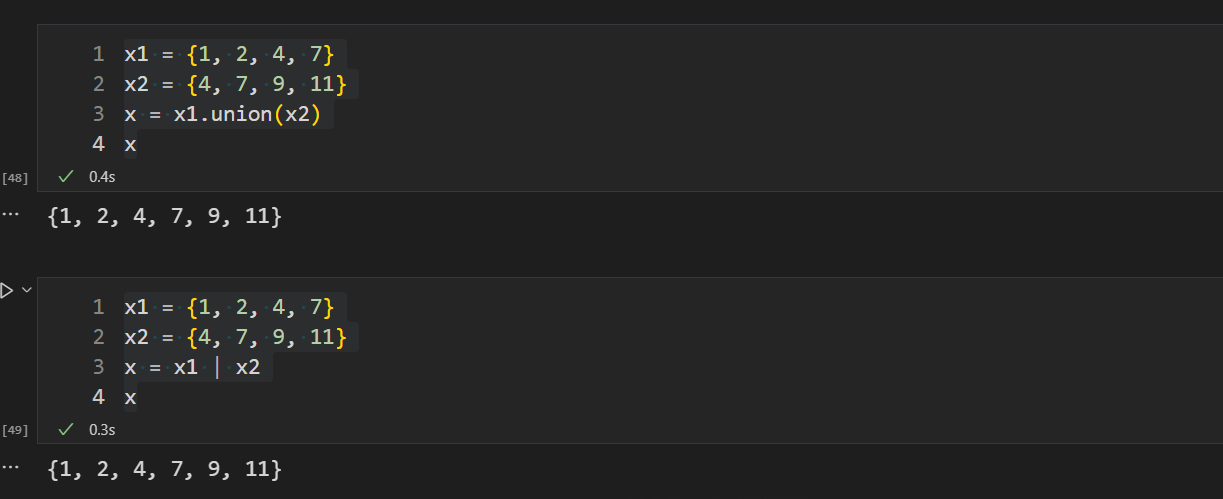
差集

A，B是两个集合，由所有属于A且不属于B的元素组成的集合，叫做集合A减集合B, 即为集合A对集合B的差集，相应的也有集合B对集合A的差集。

A对B的差集

x1 = {1, 2, 4, 7}
x2 = {4, 7, 9, 11}
x = x1.difference(x2)
x

或

x1 = {1, 2, 4, 7}
x2 = {4, 7, 9, 11}
x = x1 - x2
x

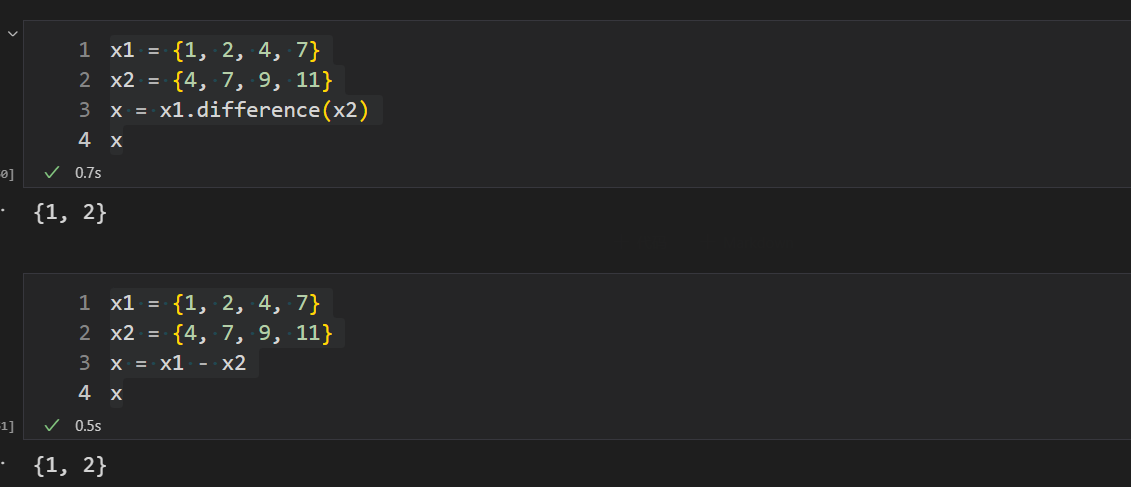
B对A的差集

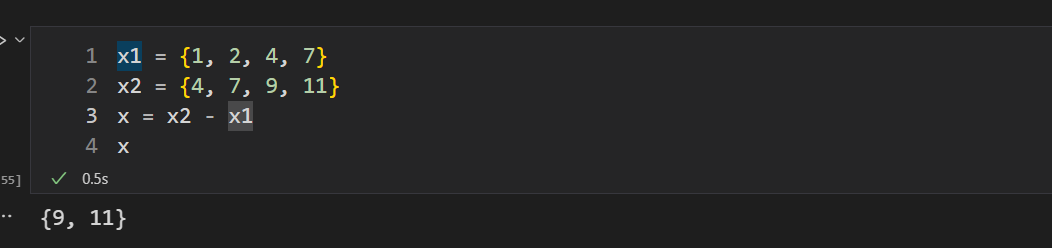
x1 = {1, 2, 4, 7}
x2 = {4, 7, 9, 11}
x = x2.difference(x1)		# 或x = x2 - x1
x

对称差集

集合A与集合B的对称差集定义为集合A与集合B中所有不属于A∩B的元素的集合，记为A△B

x1 = {1, 2, 4, 7}
x2 = {4, 7, 9, 11}
x = x1.symmetric_difference(x2)     # 或x = x1 ^ x2
x

3.5 集合推导式

{输出值 for 遍历的元素 in 列表变量 if 条件语句}

与字典的区别

{key:value for 遍历的元素 in 列表变量 if 条件语句}

字典推导式的输出为键值对，集合的输出为值。

x = {4, 1, 3, 4, 1, 2}
y = {k for k in x if k >= 2}
y

4. 总结

以上就是关于集合的基础用法，欢迎大家讨论交流~

推荐阅读：

写在末尾：

博客简介：专注AIoT领域，追逐未来时代的脉搏，记录路途中的技术成长！
专栏简介：本专栏的核心就是：快！快！快！2周快速拿下Python，具备项目开发能力，为机器学习和深度学习做准备。
面向人群：零基础编程爱好者
专栏计划：接下来会逐步发布跨入人工智能的系列博文，敬请期待
Python零基础快速入门系列
快速入门Python数据科学系列
人工智能开发环境搭建系列
机器学习系列
物体检测快速入门系列
自动驾驶物体检测系列
…