【p2p、分布式，区块链笔记 Blockchain】论文阅读 行为证明 PoB & DeFi共识模型 Proof-of-Behavior: Behavior-Driven Consensus

paper	code
Proof-of-Behavior: Behavior-Driven Consensus for Trustworthy Decentralized Finance	None

• 摘要——当前的区块链协议（例如，工作量证明和权益证明）虽然能够保护账本安全，却无法量化验证者的可信度，从而可能纵容隐蔽的不当行为——这在去中心化金融（DeFi）环境中尤其具有破坏性。文章提出了行为证明（Proof-of-Behavior, PoB）这一共识模型来处理这些问题。

I. INTRODUCTION

• 信任是去中心化系统的基石。传统共识协议，如工作量证明（PoW）和权益证明（PoS），通过大规模计算或资本投入来建立信任，但往往无法捕捉参与者的行为可信度。

• 通过将共识权力与行为挂钩，PoB形成了一个自我强化的信任网络（Web-of-Trust）。

• 本文提出了四项关键贡献：

  • 行为驱动的共识模型。我们通过一个分层效用函数对PoB进行形式化定义，该函数量化每一次行为（包括动机与结果），并引入一个活跃度评分来追踪节点的主动参与程度，以及一个动态权重规则，根据各验证者近期的行为实时更新其影响力权重 $W_i$。

  • 去中心化验证与惩罚机制。通过一种基于节点互查的“看门狗”机制，实现对行为的集体验证；一旦超级多数节点标记某行为为恶意，该行为者的权重将根据其造成损害的程度被相应削减。

  • 纳什稳定的奖励机制。我们设计了一种收益分配公式，能够产生诚实行为的纳什均衡：当其他验证者保持诚实的情况下，任何理性的验证者都无法通过偏离诚实策略来提高其长期收益。

  • 在去中心化金融场景中的实证评估。针对贷款欺诈检测、基于声誉的加权验证以及对抗性攻击等场景的模拟实验表明，与权益证明（PoS）相比，PoB能有效限制共谋行为、遏制欺诈，并更公平地分配奖励，且不会带来显著的吞吐量损失。

II. RELATED WORK

……

III. PROOF-OF-BEHAVIOR MODEL AND METHODOLOGY

• 行为证明（Proof-of-Behavior, PoB）是一种新颖的、以行为驱动的共识与激励机制，旨在奖励遵守协议的行为，并抑制恶意行为。本节详细介绍PoB模型与方法，其核心是一个多层级的行为评分系统以及相应的激励结构。我们阐述五个关键组成部分：（i）行为的分层效用评分，（ii）动态权重自适应机制，（iii）活跃度与参与度评分方案，（iv）去中心化验证与惩罚机制，以及（v）纳什稳定的奖励分配策略。

A. 分层效用评分

• 网络中的参与者所采取的每一项行为都可能具有不同层面的价值。PoB通过一个分层效用模型来捕捉这一点，该模型将参与者执行某项行为的原因（其动机）与其行为所达成的结果（成效）区分开来。形式上，验证者$i$执行的每一项行为B会产生一个总效用：

$$U_{\text{total}}(B)=U_{\text{motivation}}(B)+U_{\text{behavior}}(B)(1)$$

• 动机效用。我们考虑J种可能的动机类型（例如，经济激励、帮助网络的愿望、利他主义等）。令 $M_j$ 表示行为B背后第j种动机的强度。每种动机类型都有一个对应的权重 $w_j$（这些权重由系统设计者设定，且总和为1,满足 ${\sum }_j{w}_j=1$）。假设有$J$种动机类型，其强度为 $M_j$，设计者设定的权重为 $w_j$：

$$U_{\text{mot}}(B)=\sum _{j=1}^J{M}_j{w}_j(2)$$

• 结果效用。行为结果效用：令 $U_b$ 表示行为B的基础效用——即该行为结果对系统带来的收益的原始度量。例如，添加一个有效区块的基础效用可能与所包含的交易数量成正比，而验证他人区块的行为则可能具有较小的基础效用。我们通过两个因子对这一基础效用进行调整：一个情境权重因子 $\varphi (t;S,C)$ 和一个活跃度因子 $\alpha$。

  • 函数 $\varphi (t;S,C)$ 依赖于行为发生的时间 $t$、参与者状态 $S$（例如，其经验水平或过往记录）以及上下文环境 $C$（例如，网络负载或紧急程度）。这使得PoB能够根据具体情况对行为赋予不同的价值。

  • 同时，$\alpha \in [0,1]$ 用于衡量该行为的主动性和自愿程度（例如，节点自主发起的行为 vs. 仅在被提示后才执行的行为）。

  • 我们定义如下：令 $U_b$ 表示行为B的基础收益；令$\varphi (t;S,C)\in [0,1]$ 反映行为在时间和情境上的相关性，$\alpha \in [0,1]$ 反映行为的主动性：

$$U_{\text{beh}}(B)=U_b\cdot \varphi (t;S,C)\cdot \alpha (3)$$

• 根据上述定义，参与者所执行的每一项行为 B 都会产生一个数值化的效用 $U_{\text{total}}(B)$。将参与者$i$ 在某一时间段内（例如，一个纪元 epoch）执行的所有行为的 $U_{\text{total}}(B)$ 相加，即可得到该参与者在该时段内的累积效用得分 $U_i$。

• 这种分层方法借鉴了决策系统中的多准则评估思想：PoB 不仅统计行为的数量，还深入考察行为的质量、背景和意图。PoB 采用半监督模型对稀疏的行为轨迹进行标注，这与近期的相关综述研究[19]相一致。因此，系统能够公平地比较不同类型的行为贡献。例如，一个参与者可能执行了较少但影响力极高的行为（产生少数几项$U_{\text{total}}$很大的行为），而另一个参与者可能执行了大量微小但有益的行为（产生多项$U_{\text{total}}$ 适中的行为）——PoB 的评分机制能够恰当地累积这两类贡献。

• 纪元得分。在第 t 个纪元，参与者的累积效用为：
  $$U_i(t)=\sum _{B\in \text{epoch }t}{U}_{\text{total}}(B)$$

B. 动态权重自适应

• 效用得分直接决定每个验证者的共识权重。在PoB中，每个验证者 i 拥有一个权重 $W_i$，代表其当前的影响力——该权重用于领导者选举、投票和奖励分配，类似于其他共识协议中的作用。关键区别在于，在PoB中，权重是动态的，反映的是近期行为，而非固定不变。这一设计确保了“良好行为能及时得到奖励，而不良行为则会迅速导致影响力的下降”。

• 具体而言，我们在每个纪元（或轮次）结束时更新 $W_i$，更新依据是节点 i 在该纪元内对总效用的贡献比例。一种简单的自适应加权方案如下：

$$W_i(t+1)=(1-\rho )W_i(t)+\rho \frac{U_i(t)}{{\sum }_k{U}_k(t)},0\le \rho \le 1.(4)$$

• 其中，$W_i(t)$ 是节点 i 进入第 t 个纪元时的权重，$U_i(t)$是其在第 t 个纪元中获得的总效用。参数 $0\le \rho \le 1$是一个平滑因子，用于控制权重调整的速度。

• 公式（4）本质上定义了一种加权移动平均：保留一部分（$1-\rho$）的旧权重，同时用一部分（$\rho$）根据节点在上一个纪元的表现进行更新（具体为其在该纪元中所有节点产生的总效用中所占的份额）。如果$\rho$ 较大（接近1），系统会快速“遗忘”过去，权重主要反映近期行为；如果 $\rho$ 较小，权重变化更缓慢，对过去的贡献记忆更长。（哈哈，怎么感觉像优快云之前被吐槽的积分机制）

• 为何采用动态权重？

  • 这一机制意味着，一个初始权重较低的参与者，可以通过持续贡献有益行为而提升其影响力；反之，一个高权重参与者若变得懒惰或恶意，也会失去影响力。这解决了简单权益证明（PoS）的一个关键缺陷：PoB不会永久固化早期领导者的地位，而是持续对所有参与者进行重新评估。同时，该机制也有助于防止权力集中——为了避免高权重节点始终主导领导者选举的情况，模型可以在选择算法中引入轻微的随机化或衰减因子（记为 δ）。例如，在选举区块提议者时，PoB可以不完全按照 $W_i/{\sum }_k{W}_k$ 的严格比例进行，而是为每个活跃节点提供一个基础中选概率 δ，其余概率再按权重分配。这确保了即使是低权重节点也有机会偶尔获得领导权，从而保持其参与积极性，防止形成固化的寡头垄断。

  • 对激励机制的影响。每一轮结束后，参与者会立即看到其权重 $W_i$ 根据其行为得到调整。诚实且活跃的节点会发现 $W_i$ 逐步上升，从而在下一轮中获得更高的奖励或领导机会；而行为不当或怠惰的节点则会看到 $W_i$ 下降。这种快速反馈机制闭合了激励循环：良好行为带来更多未来收益，不良行为则导致权力丧失。在实践中，动态信任管理使得诚实节点的影响力能够迅速超越恶意节点。因此，动态权重是PoB（借鉴先前基于信任系统理念）实现“激励诚实行为、遏制恶意攻击”的关键组成部分。

C. 活跃度评分

• 尽管 $U_{\text{total}}$ 能够衡量行为的价值，PoB 还会考虑每个参与者在支持系统运行中的活跃程度和参与积极性。我们为每个参与者 i 定义一个活跃度评分 $A_i$，用于量化其整体参与水平和主动性。该指标通过追踪参与者随时间推移的参与模式，补充了效用评分。具体而言，$A_i$ 旨在捕捉行为的以下几个不同方面：

  • 频率（f）：参与者 i 执行有益行为的频率如何？例如，统计 i 在每个纪元内验证的交易数量或提出的区块数量，然后根据预期速率或网络平均水平进行归一化。

  • 主动性（$\bar{\alpha }$）：参与者 i 的行为有多主动和自愿？我们使用其所有行为的平均主动性得分 ${\bar{\alpha }}_i$，其中每个行为级别的 $\alpha$ 值反映其行为的前瞻性与自发性。

  • 多样性（d）：参与者 i 是否参与了多种角色和任务——例如提出区块、验证他人区块、提供预言机数据等——还是仅专注于单一活动？更高的多样性表明其对网络的支持更广泛、更具韧性。

• 该活跃度评分 $A_i$ 可综合上述维度，例如通过加权求和或其他聚合函数（如几何平均）进行计算，从而全面反映节点的参与质量，避免“搭便车”或单一功能化倾向，进一步增强系统的公平性与鲁棒性。

• 一种简单的形式是将这些方面组合为一个加权和。例如，令 $S_i$ 表示参与者 i 在某一时间段内的行为次数，$\bar{S}$ 表示网络中每个参与者的平均行为次数；令 ${\bar{\alpha }}_i$ 表示 i 所有行为的平均主动性，$d_i$ 表示归一化的多样性指数（0 表示活动范围非常狭窄，1 表示活动非常多样化）。则我们可以定义：

$$A_i={\beta }_1\frac{S_i}{\bar{S}}+{\beta }_2{\bar{\alpha }}_i+{\beta }_3{d}_i,\sum _{m=1}^3{\beta }_m=1,(5)$$

• 其中 $S_i$ 代表行为频率，${\bar{\alpha }}_i$ 代表平均主动性，$d_i$ 代表归一化的多样性指数。$A_i$ 可用于提升奖励或触发异常警报。

• 在这个示例模型中，对于那些比平均水平更活跃、表现出高度主动性，并以多种方式做出贡献的参与者，其 $A_i$ 值会较高。相反，如果某人频繁执行大量琐碎行为（$S_i$ 高），但主动性低（仅在被提示时才行动）、多样性差（总是执行同一任务），其 $A_i$ 值也不会很高，因为低 ${\bar{\alpha }}_i$ 和低 $d_i$ 会拉低总分。这防止了仅靠行为数量来“刷分”的行为——系统鼓励的是全面且主动的参与，而不仅仅是高产。

• 文章在 PoB 中以多种方式使用$A_i$：

  • 奖励乘数：$A_i$ 可作为权重或奖励计算中的额外因子。例如，参与者的最终收益可按 $(1+ϵ{)}^{A_i}$ 进行缩放（$ϵ$ 为较小常数），从而为高度活跃的节点提供适度奖励。

  • 异常检测：$A_i$ 还可作为异常行为的指示器。当某个节点的行为频率 $f$ 异常高，但其主动性或多样性却非常低时，该行为可能是人为操纵的（例如脚本化操作或刷指标）。此类情况可被标记以供审查，或限制其奖励，从而抑制重复性、低质量的行为。

• 总之，活跃度评分 $A_i$ 在原始效用贡献的基础上，进一步衡量了参与的质量，从而增强了PoB机制。它鼓励广泛而主动的参与，同时抑制表面化或完全由脚本驱动的浅层行为。 In summary, the activeness score Ai strengthens PoB by recognizing the quality of engagement in addition to (In addition, 此外) raw utility contribution. This encourages broad, voluntary participation and discourages superficial or purely scripted activity.

D. 去中心化验证与惩罚机制 Decentralised Verification and Punishment

• 任何共识机制若缺乏对不当行为的处理方式，都是不完整的。因此，PoB采用了一种完全去中心化的“看门狗”模式：由验证者社区自身充当裁判，无需任何中心化权威，即可检测并惩罚违规者。

• 当发生可疑事件时——例如某验证者提出了一个无效区块，或未能履行其应尽职责——PoB会从其他参与者中随机选出一个验证委员会，对该事件进行审查。这些节点独立评估该事件。

• 假设参与者X被怀疑存在不当行为。每个观察到该行为的节点会独立判断X的行为是否恶意；令 ${\varphi }_X$ 表示标记该行为为恶意的观察者所占的比例。如果${\varphi }_X\ge \theta$，其中$\theta$ 为预设的阈值（通常为2/3），则网络通过共识确认该违规行为成立。

• 一旦违规行为被确认，该行为将被记为负效用，并对X的权重施加惩罚 $\Delta W$：

$$\text{如果 }{\varphi }_X\ge \theta ,W_X\leftarrow W_X-\Delta W.(6)$$

• 其中，$\Delta W=p\cdot U_b$，其大小与违规的严重程度成正比（$U_b$ 为该行为的基础效用，$p$ 为惩罚系数）。对于双签等严重攻击行为，甚至可将其全部权重清零（全额罚没）。

• 惩罚机制是可调节的：轻微违规行为将受到较小的 $\Delta W$（相当于警告），而严重攻击则会受到较大的 $\Delta W$ 并可能被暂时停权。对于屡次违规者，惩罚系数 $p(f_i)$ 将逐步加重，从而遏制持续性的滥用行为。

• 由于单个节点的判断不足以定罪，攻击者无法仅凭自身诬陷诚实的验证者，也无法在不腐蚀超级多数节点的情况下逃避惩罚——这在难度上等同于直接攻破共识机制本身。通过轮换制或全体节点参与的委员会机制，监督过程具备高度鲁棒性。

• 关键的是，PoB的惩罚不仅限于一次性奖励扣除，而是直接降低违规者未来的共识影响力。因此，理性的节点会意识到：作弊虽可带来短期收益，但将导致长期影响力的损失，从而进一步强化了诚实行为的动机。

E. 纳什稳定奖励分配 Nash-Stable Reward Distribution

• 一个设计良好的奖励机制对于将验证者的激励与诚实行为保持一致至关重要。PoB 在每个纪元根据两个目标分配奖励：公平性（奖励与贡献成正比）和包容性（鼓励广泛参与），同时维持一种有利于诚实行为的博弈论均衡。
• a) 奖励设计：在每个纪元结束时，协议分配的总奖励 $R_{\text{tot}}$ 由两部分组成：
  • （i）向每个活跃验证者（$U_i>\beta$）$发放的基础津贴$ $R_{\text{base}}$，以及（ii）$按权重比例分配的额外奖励$ $R_{\text{bonus}}=R_{\text{tot}}-N_a{R}_{\text{base}}$。具体分配公式如下：

$$R_i=R_{\text{base}}+R_{\text{bonus}}\cdot \frac{w_i}{{\sum }_{k\in A}{w}_k},(6)$$

• 其中 $A$ 是活跃验证者集合（$|A|=N_a$），$w_i$ 是验证者 $i$ 的行为权重。

• b) 权重更新：权重通过指数移动平均进行更新：

$$w_i(t+1)=(1-\rho )w_i(t)+\rho \frac{U_i(t)}{{\sum }_k{U}_k(t)},0<\rho <1,(7)$$

• 如果验证者 $i$ 被发现存在不当行为，则对其权重进行乘法式罚没：$w_i\leftarrow {\rho }_p{w}_i$（其中 ${\rho }_p<1$）。

激励相容性的形式化证明（后面部分总结：c和e部分为证明，d为a的等价表述）：

• c) 设定：无限轮次博弈，折现因子为 $\delta \in (0,1)$。每轮中，验证者可选择诚实行为 $H$ 或不诚实行为 $D$。任何偏离行为将以概率1被检测到，并触发（i）即时惩罚 $P$，以及（ii）权重下降因子 ${\rho }_p<1$。

• 令 $\Delta R$ 表示偏离所能获得的最大单轮额外收益，并定义：

$$L:=P+\frac{(1-{\rho }_p)\mathbb{E}[R_i^{\text{honest}}]}{1-\delta }\text{（因权重降低导致的未来收益损失）}$$

• 该表达式 $L$ 衡量了偏离行为带来的长期损失，包括即时罚金 $P$ 和由于权重下降而折现的未来收益减少。若长期损失 $L$ 大于短期收益 $\Delta R$，则诚实行为将成为占优策略，从而证明该机制是激励相容的。

• 假设 1：$L>\Delta R$（惩罚和未来损失超过任何短期收益）。

• 定理 1（诚实的纳什均衡）：在假设 1 成立的条件下，所有验证者在每一轮都保持诚实的策略组合构成了PoB博弈的一个严格纳什均衡。

• 证明：固定一个验证者 $i$，并假设其他所有验证者均保持诚实。如果 $i$ 在第 $t$ 轮首次发生偏离行为，则其净效用变化为：

$${\text{NetGain}}_i=\underset{\text{即时收益}}{\underbrace{\Delta R}}-\underset{\text{惩罚 + 未来损失的现值}}{\underbrace{L}}<0\text{（由假设1保证）}$$

• 因此，任何偏离行为都会降低 $i$ 的折现总收益。通过对最早偏离轮次进行归纳推理可知，任何包含不诚实行为 $D$ 的策略所获得的总效用，均低于始终诚实的策略。因此，对每个验证者而言，保持诚实是其最优响应。这证明了“全员诚实”的策略组合构成一个纳什均衡。

d) 奖励分配：在第 $t$ 个纪元，协议通过两个部分分配总奖励 $R_{\text{total}}$（包括区块奖励、交易手续费等）：

• 基础奖励：所有效用满足 $U_i>\beta$ 的活跃验证者，均可获得一个固定的基础参与奖励 $R_{\text{base}}$。

• 比例奖金：剩余部分 $R_{\text{bonus}}=R_{\text{total}}-N{R}_{\text{base}}$（其中 $N$ 为活跃验证者数量），按权重比例分配：

$$R_i=R_{\text{base}}+R_{\text{bonus}}\times \frac{W_i}{{\sum }_{k\text{ active}}{W}_k}.(7)$$

第一项确保每个诚实节点都能获得最低收益，防止小节点因收益过低而退出；第二项则与权重 $W_i$ 成正比，在奖励贡献更大的节点的同时，避免了无约束的“富者愈富”效应。

• e) 激励相容性（纳什均衡）：如果在假设所有其他验证者均保持诚实的前提下，满足：

$$\mathbb{E}[R_i(\text{honest})]\ge \mathbb{E}[R_i(\text{cheat})],(8)$$

• 则诚实行为构成一个纳什均衡。

• PoB 通过以下机制确保这一条件成立：

  • 1. 动态权重与惩罚机制：作弊将导致权重被削减（$\Delta W=p{U}_b$），其对未来收入的长期损失超过任何短期收益。
  • 2. 随机化领导者选择：在提议者选择中引入轻微随机性 $\delta$，消除可预测的“安全作恶窗口”，增加攻击的不确定性。
  • 3. 包容性基础奖励：失去权重意味着可能失去固定的基础奖励 $R_{\text{base}}$，即使低权重节点也有实际利益需要保护，从而增强其诚实动机。
  • 4. 抗共谋设计：任何低于共识阈值的共谋团体都会被标记并集体惩罚，使得大规模协同作恶无利可图。

• 因此，理性的验证者通过保持诚实可最大化其长期收益，从而将个体激励与系统的整体安全目标保持一致。

• 总结：分层行为评分、自适应权重、包容性激励与去中心化监督共同构建了一个自我调节的系统：诚实参与者不断积累影响力和奖励，而违规者则迅速被边缘化，从而使诚实行为成为PoB中的主导策略。

• 总之，行为证明（Proof-of-Behavior）模型将分层行为评分、自适应权重调节、积极参与激励、去中心化监督以及公平的奖励分配机制有机整合。这些组件共同构建了一个自我调节的激励系统：表现良好的参与者能够稳步积累更高的评分与奖励，而行为不当者则会被迅速识别并受到惩罚。这些机制的协同作用形成了一种稳健的均衡状态，使得诚实、合作的行为对所有参与者而言都是最具收益的策略，从而增强了网络的安全性与公平性。

IV. 去中心化金融案例 EVALUATION AND CASE STUDIES IN DEFI CONTEXT

• 通过两个具有代表性的去中心化金融（DeFi）案例研究来评估行为证明（Proof-of-Behavior, PoB）模型。所有仿真均在配备8核Intel CPU和16GB内存的机器上使用Python 3.10执行。网络延迟模型（随机延迟，均值为50毫秒）用于模拟消息传播过程。每个场景均进行了30次独立的蒙特卡洛试验，并使用固定随机种子；我们报告均值及95%置信区间。

• 作为对比，我们实现了一个现代权益证明（PoS）基线方案，该方案采用基于权益权重的领导者选择机制，并对恶意行为实施罚没惩罚。关键性能指标包括：

  • 诈骗接受率（fraud-acceptance rate），
  • 提议者公平性（Gini系数），
  • 区块延迟（block latency），
  • 权重自适应速度（weight-adaptation speed），
  • 避免的累计经济损失（cumulative economic loss averted）。

• 文章提出以下五个案例研究，以展示PoB在100个和1000个验证者规模网络中的可扩展性：
  （A）DeFi贷款诈骗攻击场景，
  （B）共识公平性场景，
  （C）真实以太坊DeFi数据回放（基于真实世界行为的验证），
  （D）额外的对抗弹性测试（女巫攻击、长程分叉、提议者恶意阻挠），
  （E）参数敏感性分析。

A. Case Study A: Loan-Fraud Attack Mitigation

a) 场景：我们模拟一个去中心化金融（DeFi）借贷平台，其中恶意行为者试图通过两种策略实施欺诈：隐蔽攻击（stealth attacks）和女巫突发攻击（Sybil-burst attacks）。在隐蔽攻击中，一个验证者偶尔发起但高价值的欺诈性交易（例如，抵押不足的贷款或闪电贷攻击），企图逃避检测。在女巫突发攻击中，攻击者将其资源分散到多个共谋地址（女巫身份），同时发起大量小规模的欺诈尝试。这些攻击模式用于检验PoB在不同行为模式下检测和惩罚恶意行为的能力。

b) 指标：我们定义诈骗接受率（Fraud-Acceptance Rate, FAR）为：

$$\text{FAR}=\frac{\text{被接受的欺诈交易数量}}{\text{尝试的欺诈交易数量}},(8)$$

• 并测量避免的累计经济损失，即PoS基线与PoB之间的总经济损失之差，反映PoB通过早期欺诈检测所保护的价值。

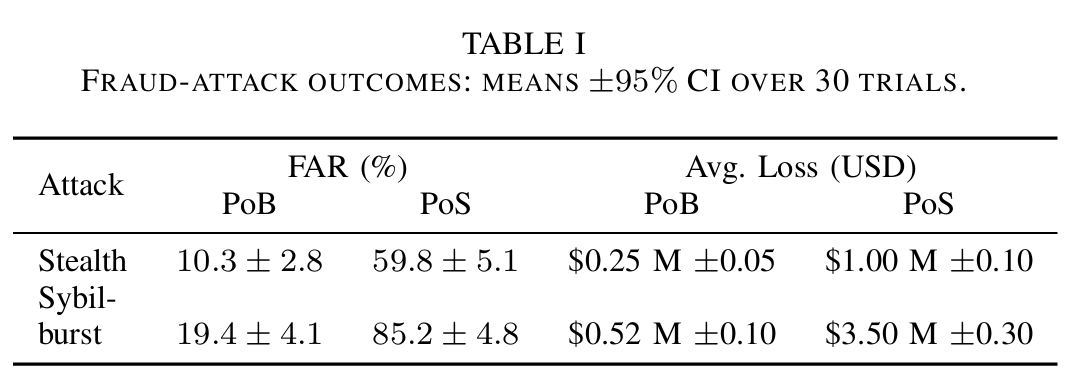
c) 结果：PoB在两种攻击模式下均显著降低了欺诈成功率。对于隐蔽攻击，PoB实现的FAR约为 $10\%\pm 3\%$，而PoS+罚没基线的接受率高达 $60\%\pm 5\%$。在30次试验中，PoB避免了约75%的潜在损失；若在基线系统中隐蔽攻击者成功窃取100万美元，在PoB中仅能获得25万美元，从而节省75万美元。当验证者数量扩展至1000时，防御能力进一步增强（PoB的FAR ≈ 8%，基线 ≈ 62% ± 4%）。

• 对于女巫突发攻击，PoB的FAR约为 $20\%\pm 4\%$，而基线系统高达 $85\%\pm 5\%$。PoB的快速集体响应机制在恶意节点首次提交恶意区块后即标记多个女巫地址；其行为评分 $U_i(t)$ 迅速转为显著负值，权重 $W_i$ 因惩罚系数 $p$ 被立即削减，从而在后续区块中丧失影响力。即使在1000个验证者的规模下，FAR仍保持低位（约18%，置信区间重叠），显示出良好的可扩展性。
  

• PoB的权重自适应机制使系统在攻击爆发后仅需几个区块即可收敛至安全状态，而基线系统则需等待罚没机制或应用层干预，响应滞后。除了有效阻止攻击，PoB的性能开销也处于可接受范围。区块延迟（确认区块所需时间）仅略有增加：PoB平均为3.3秒，PoS为3.0秒，额外开销约10%，尽管增加了行为验证步骤，但差异在统计上不显著（95%置信区间重叠）。

• 此外，PoB的累积权重调整机制能迅速隔离恶意行为者。在隐蔽攻击试验中，恶意验证者的权重在被检测到后的两轮内即下降约90%，彻底丧失提出新区块的能力。相比之下，在PoS系统中，同一验证者仍会持续被选为提议者，直到较晚才触发罚没，从而延长了损害窗口。

• 这些结果表明，PoB基于社区驱动的执行机制能够及时遏制欺诈行为，避免大规模经济损失，同时保持系统的活性与吞吐量。

B. 案例研究B：提议者公平性与适应性对比PoS

• 暂略