leetcode算法每天一题016：最接近的三数之和

原创已于 2023-07-04 14:42:00 修改 · 441 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #算法 #数据结构

于 2022-11-09 10:50:47 首次发布

语言学习笔记专栏收录该内容

193 篇文章

订阅专栏

这篇博客介绍了如何利用双指针法解决寻找数组中三数之和最接近目标值的问题。首先对数组进行排序，然后遍历数组，用双指针分别指向第二个和第三个数，根据三数之和与目标值的关系调整指针位置，不断更新最接近的和。最后返回结果。代码实现中涉及到了优化和错误修复。

题目描述

给你一个长度为 n 的整数数组 nums 和 一个目标值 target。请你从 nums 中选出三个整数，使它们的和与 target 最接近。

返回这三个数的和。

假定每组输入只存在恰好一个解。

解

因为只需要三数之和，所以只需要维持一个距离result即可，然后距离有正负，同时维持了一个flag符号，得到三数之和target+ flag*result

class Solution {
public:
    //vector<vector<int>> threeSum(vector<int>& nums) {
    int threeSumClosest(vector<int>& nums, int target) {
        int result = 1000;
        int flag = 1;
        sort(nums.begin(), nums.end());
        // 找出a + b + c = 0
        // a = nums[i], b = nums[left], c = nums[right]
        for (int i = 0; i < nums.size()-2; i++) {
            // a去重，如果不去重会出现两个[-1，0，1]的结果
            // 如果当前指到的数字上次已经用过就跳过
            if (i > 0 && nums[i] == nums[i - 1]) { // nums[i] == nums[i + 1] 会丢失[-1,-1,2]这个结果
                continue;//跳过或i++
            }
            int left = i + 1;
            int right = nums.size() - 1;
            while (right > left) {
                // 去重复逻辑如果放在这里，0，0，0 的情况，可能直接导致 right<=left 了，从而漏掉了 0,0,0 这种三元组
                /*
                while (right > left && nums[right] == nums[right - 1]) right--;
                while (right > left && nums[left] == nums[left + 1]) left++;
                */
                if (nums[i] + nums[left] + nums[right] > target) {
                    //先执行这一句
                    if(nums[i] + nums[left] + nums[right] - target < result){
                        result = nums[i] + nums[left] + nums[right] - target ;
                        flag = 1;
                    }
                    right--;
                    
                } else if (nums[i] + nums[left] + nums[right] < target) {
                    if(target - nums[i] - nums[left] - nums[right] < result){
                        result = target - nums[i] - nums[left] - nums[right];
                        flag = -1;
                    }
                    left++;
                    
                } 
                else {
                    //result.push_back(vector<int>{nums[i], nums[left], nums[right]});

                    // 去重逻辑应该放在找到一个三元组之后
                    // while (right > left && nums[right] == nums[right - 1]) right--;
                    // while (right > left && nums[left] == nums[left + 1]) left++;

                    // 找到答案时，双指针同时收缩
                    // right--;
                    // left++;
                    return target;
                }
            }

        }
        return target+ flag*result;
    }
};

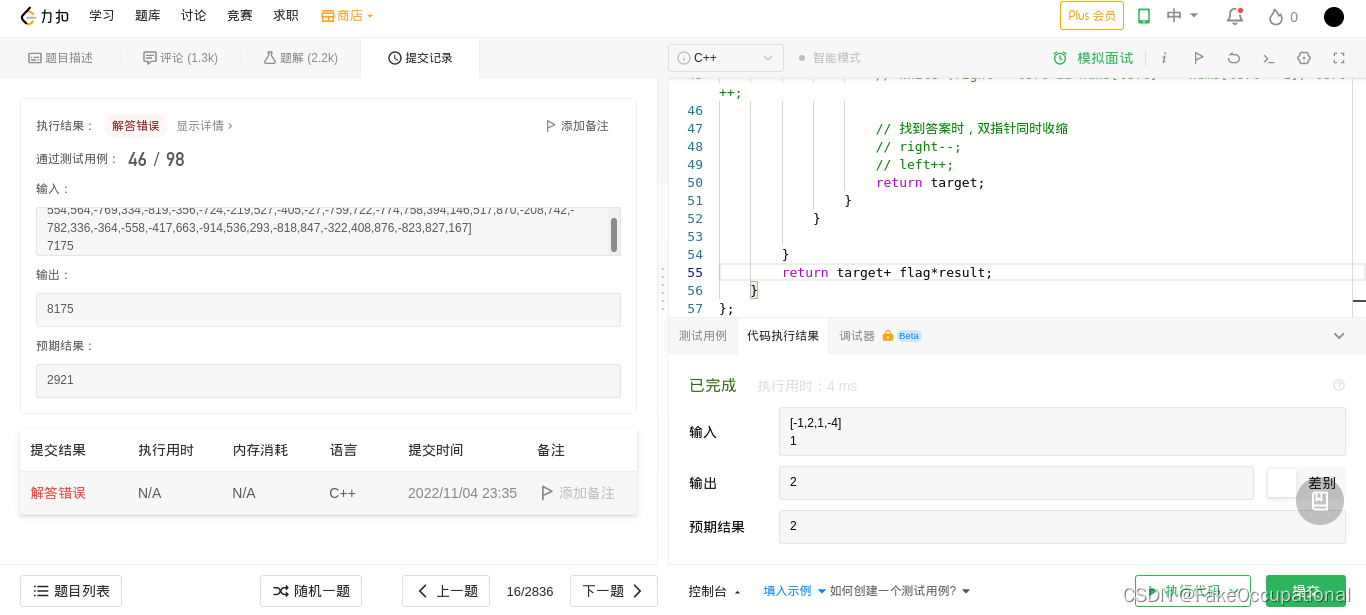
改了一下初始化

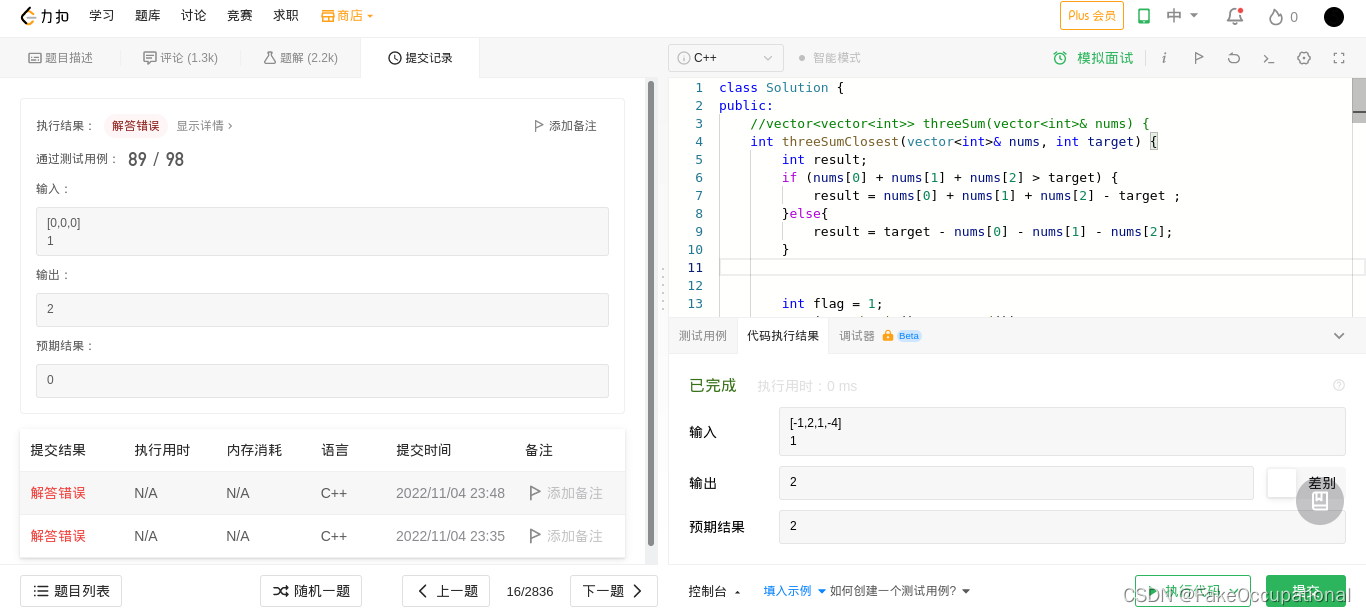
在这里插入图片描述

还有一个错误，再修改一下：

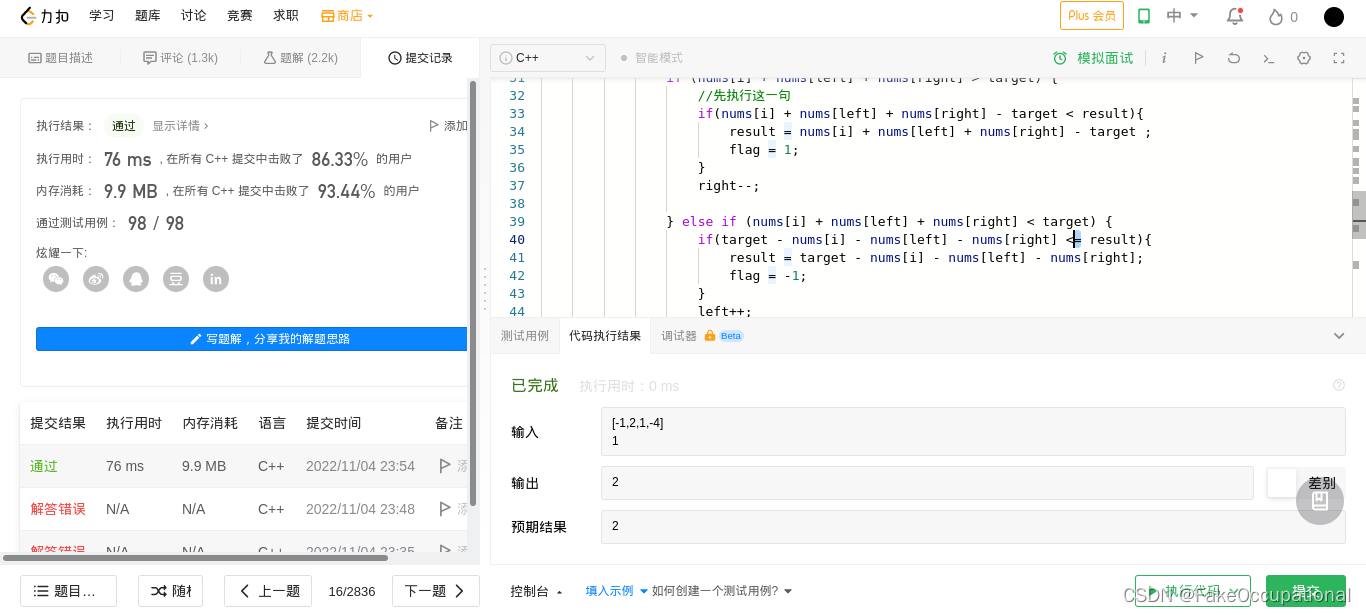
在这里插入图片描述

class Solution {
public:
    //vector<vector<int>> threeSum(vector<int>& nums) {
    int threeSumClosest(vector<int>& nums, int target) {
        int result;
        if (nums[0] + nums[1] + nums[2] > target) {
            result = nums[0] + nums[1] + nums[2] - target ;
        }else{
            result = target - nums[0] - nums[1] - nums[2];
        }

        
        int flag = 1;
        sort(nums.begin(), nums.end());
        // 找出a + b + c = 0
        // a = nums[i], b = nums[left], c = nums[right]
        for (int i = 0; i < nums.size()-2; i++) {
            // a去重，如果不去重会出现两个[-1，0，1]的结果
            // 如果当前指到的数字上次已经用过就跳过
            if (i > 0 && nums[i] == nums[i - 1]) { // nums[i] == nums[i + 1] 会丢失[-1,-1,2]这个结果
                continue;//跳过或i++
            }
            int left = i + 1;
            int right = nums.size() - 1;
            while (right > left) {
                // 去重复逻辑如果放在这里，0，0，0 的情况，可能直接导致 right<=left 了，从而漏掉了 0,0,0 这种三元组
                /*
                while (right > left && nums[right] == nums[right - 1]) right--;
                while (right > left && nums[left] == nums[left + 1]) left++;
                */
                if (nums[i] + nums[left] + nums[right] > target) {
                    //先执行这一句
                    if(nums[i] + nums[left] + nums[right] - target < result){
                        result = nums[i] + nums[left] + nums[right] - target ;
                        flag = 1;
                    }
                    right--;
                    
                } else if (nums[i] + nums[left] + nums[right] < target) {
                    if(target - nums[i] - nums[left] - nums[right] <= result){
                        result = target - nums[i] - nums[left] - nums[right];
                        flag = -1;
                    }
                    left++;
                    
                } 
                else {
                    return target;
                }
            }

        }
        return target+ flag*result;
    }
};

求解最接近的三数之和，可以运用双指针的思想。具体步骤如下：

对数组进行排序。
遍历数组，将当前元素作为三元组的第一个数，用双指针指向第二个和第三个数。
计算三个数的和，如果和等于目标值，则直接返回。
如果和小于目标值，则将左指针向右移动。
如果和大于目标值，则将右指针向左移动。
在移动指针的过程中，记录当前三个数的和与目标值之间的差值，如果差值更小，则更新最接近的三数之和。
遍历完整个数组后，返回最接近的三数之和。

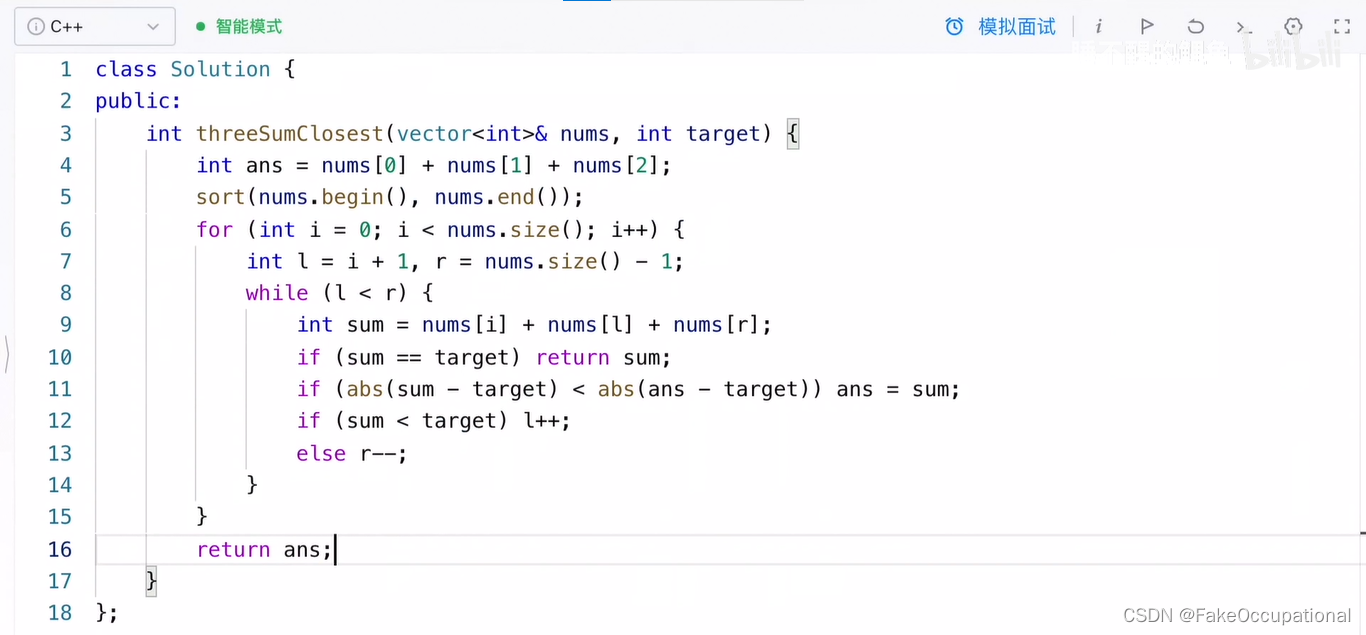
下面是求解最接近的三数之和的C++代码实现：

class Solution {
public:
    int threeSumClosest(vector<int>& nums, int target) {
        sort(nums.begin(), nums.end());
        int n = nums.size();
        int res = nums[0] + nums[1] + nums[2];
        for (int i = 0; i < n - 2; i++) {
            int l = i + 1, r = n - 1;
            while (l < r) {
                int sum = nums[i] + nums[l] + nums[r];
                if (sum == target) {
                    return target;
                } else if (sum < target) {
                    l++;
                } else {
                    r--;
                }
                if (abs(sum - target) < abs(res - target)) {
                    res = sum;
                }
            }
        }
        return res;
    }
};