参考视频链接


下图右侧为对“退出”的解释,及对于问题
m
i
n
(
x
2
+
y
2
)
满足
x
=
2
y
,
由于带入计算误差太大
,
退出带入
,
使用拉格朗日乘子方法,
然后使用识别因子的方法
,
令一阶微分
=
0
,识别出
λ
下图右侧为对“退出”的解释,及对于问题min(x^2+y^2)满足x=2y,\\ 由于带入计算误差太大,退出带入,使用拉格朗日乘子方法,\\ 然后使用识别因子 的方法,令一阶微分=0,识别出\lambda
下图右侧为对“退出”的解释,及对于问题min(x2+y2)满足x=2y,由于带入计算误差太大,退出带入,使用拉格朗日乘子方法,然后使用识别因子的方法,令一阶微分=0,识别出λ

一阶微分对应于一阶变分
一阶微分对应于一阶变分
一阶微分对应于一阶变分

带入识别因子之后可以得到不含拉格朗日乘子的泛函
带入识别因子之后可以得到不含拉格朗日乘子的泛函
带入识别因子之后可以得到不含拉格朗日乘子的泛函

总结
总结
总结

验证
验证
验证

解决之前的近似问题
解决之前的近似问题
解决之前的近似问题
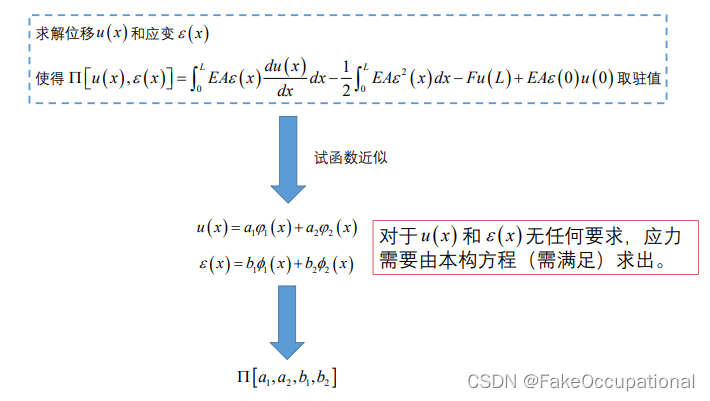
广义变分原理
广义变分原理
广义变分原理






















 33
33

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








