标定
在已知二维图像点与三维世界点的对应条件H下,求解相机模型关系中的未知参数
[
u
v
1
]
=
k
∗
A
[
r
1
,
r
2
,
r
3
,
t
]
[
X
Y
0
1
]
=
k
∗
A
[
r
1
,
r
2
,
t
]
[
X
Y
1
]
(1)
\begin{bmatrix}u\\v\\1\end{bmatrix} =k*A[r_1,r_2,r_3,t]\begin{bmatrix}X\\Y\\0\\1\end{bmatrix}=k*A[r_1,r_2,t]\begin{bmatrix}X\\Y\\1\end{bmatrix} \tag{1}
⎣⎡uv1⎦⎤=k∗A[r1,r2,r3,t]⎣⎢⎢⎡XY01⎦⎥⎥⎤=k∗A[r1,r2,t]⎣⎡XY1⎦⎤(1)
由
式
子
(
1
)
写
成
[
u
v
1
]
=
k
[
h
1
,
h
2
,
h
3
]
[
X
Y
1
]
(2)
由式子(1)写成 \begin{bmatrix}u\\v\\1\end{bmatrix} =k[h_1,h_2,h_3]\begin{bmatrix}X\\Y\\1\end{bmatrix} \tag{2}
由式子(1)写成⎣⎡uv1⎦⎤=k[h1,h2,h3]⎣⎡XY1⎦⎤(2)
由 式 子 ( 1 ) , ( 2 ) 可 得 { r 1 = k A − 1 h 1 r 2 = k A − 1 h 2 t = k A − 1 h 3 由 r 1 与 r 2 正 交 且 模 相 等 ( 都 为 1 ) 的 约 束 可 得 有 关 A − T A − 1 ( 记 为 B ) 的 方 程 M B = 0 ( M 由 H 中 元 素 确 定 ) 解 “ 其 次 方 程 ” 可 到 到 B 中 元 素 的 比 例 关 系 B = λ A − T A − 1 进 而 得 到 A 注 : B 为 6 D O F , 故 需 要 3 张 图 片 由式子(1),(2)可得\left\{\begin{array}{l} r_1=kA^{-1}h_1\\ r_2=kA^{-1}h_2\\ t=kA^{-1}h_3 \end{array}\right. \\ 由r_1与r_2正交且模相等(都为1)的约束可得\\ 有关A^{-T}A^{-1}(记为B)的方程MB=0\\ (M由H中元素确定)\\ 解“其次方程”可到到B中元素的比例关系\\ B=\lambda A^{-T}A^{-1}进而得到A\\ 注:B为6DOF,故需要3张图片 由式子(1),(2)可得⎩⎨⎧r1=kA−1h1r2=kA−1h2t=kA−1h3由r1与r2正交且模相等(都为1)的约束可得有关A−TA−1(记为B)的方程MB=0(M由H中元素确定)解“其次方程”可到到B中元素的比例关系B=λA−TA−1进而得到A注:B为6DOF,故需要3张图片
张正友标定方法
工具箱官网
1.选择camera calibration

2.填写棋盘格大小后添加图片

3.点击calibrate
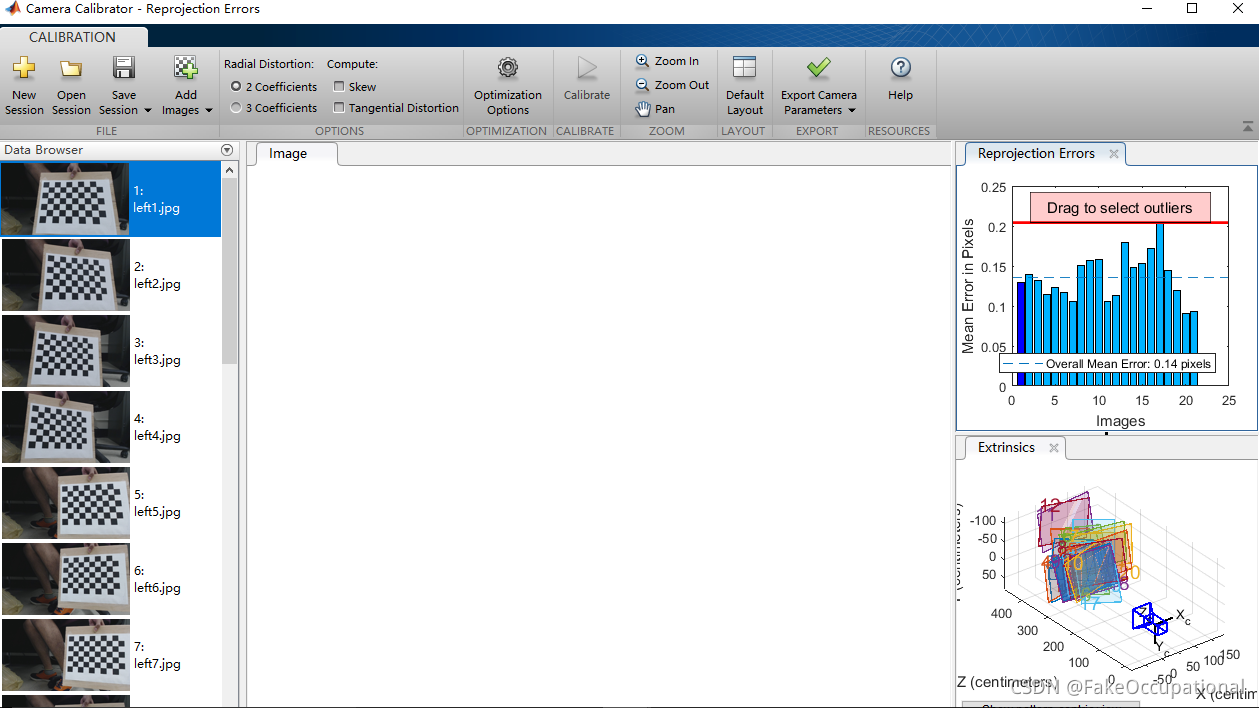
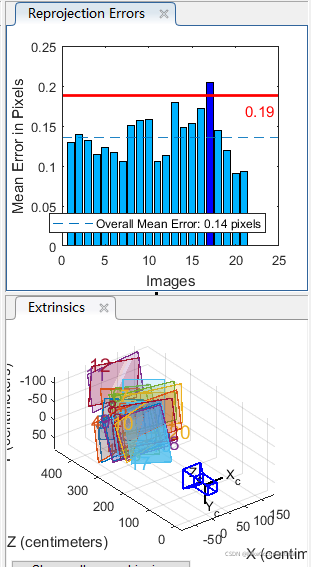
4.根据平均误差选择平面
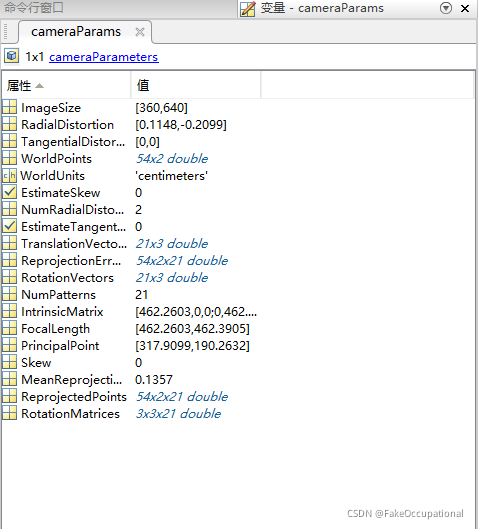
5.导出参数到工作空间,参数解释见官网

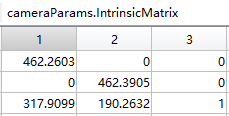





 本文解析了在二维图像与三维世界点的对应关系下,如何通过标定求解相机模型中未知参数的过程,重点介绍了张正友标定方法,包括利用A矩阵和H条件,以及A-1和A^T的运算。讲解了如何通过正交性和模长约束找到相机矩阵A的参数,并说明了为何需要至少三张图片进行6自由度(DOF)的标定。
本文解析了在二维图像与三维世界点的对应关系下,如何通过标定求解相机模型中未知参数的过程,重点介绍了张正友标定方法,包括利用A矩阵和H条件,以及A-1和A^T的运算。讲解了如何通过正交性和模长约束找到相机矩阵A的参数,并说明了为何需要至少三张图片进行6自由度(DOF)的标定。
















 1027
1027

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








