图的应用——Prim算法最小生成树

1．实验目的

（1）掌握图的相关概念，包括图、有向图、无向图、子图、连通图、度、入度、出度、简单回路、环等；

（2）掌握图的各种存储结构，包括邻接矩阵和邻接表等；

（3）掌握图的基本运算，包括创建图、输出图、深度优先遍历、广度优先遍历等；

（4）掌握图的其他运算，包括最小生成树、最短路径、拓扑排序和关键路径等算法。

2．实验内容

利用Prim算法求网的最小生成树。

要求和提示：设图的顶点数为10个。为简单起见，网中边的权值设成小于100的整数，可利用C语言的rand()函数产生。

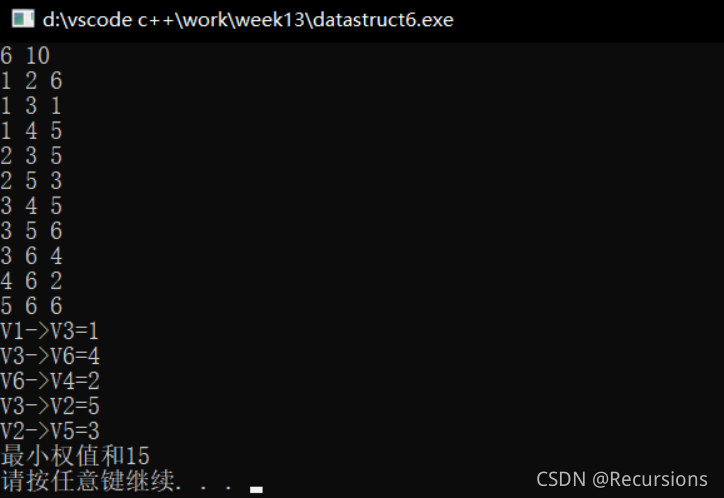
3．源程序和实验结果

#include<bits/stdc++.h>
using namespace std;

#define MAX 100
#define INF 10000

int graph[MAX][MAX];

int prim(int graph[][MAX], int n)
{
    int lowcost[MAX],closedge[MAX];
    int min_1,min_2,sum = 0;
    for(int i = 2;i <= n;i++)
    {
        lowcost[i] = graph[1][i];
        closedge[i] = 1;
    }
    closedge[1] = 0;
    for(int i =1;i <= n-1;i++)
    {
        min_1 = INF;
        min_2 = 0;
        for(int j = 1;j <= n;j++)
        {
            if(lowcost[j] < min_1&&closedge[j]!=0)
            {
                min_1 = lowcost[j];
                min_2 = j;
            }
        }
        cout << "V" << closedge[min_2] << "->V" << min_2 << "=" << min_1 <<endl;
        sum += min_1;
        closedge[min_2] = 0;
        for(int j = 1;j <= n;j++)
        {
            if(graph[min_2][j] < lowcost[j]&& closedge[j] != 0)
            {
                lowcost[j] = graph[min_2][j];
                closedge[j] = min_2;
            }
        }
    }
    return sum;
}

int main()
{
    int m,n,e,v,cost;
    cin >> m >> n;//m顶点数  n边数
    memset(graph,INF,sizeof(graph));
    for(int i = 1;i <= n;i++)
    {
        cin >> v >> e >> cost;
        graph[v][e] = graph[e][v] = cost;
    }
    int Sum;
    Sum = prim(graph, m);
    cout << "最小权值和" << Sum << endl;
    system("pause");
}