B树与B+树的区别在于:
1)在B+树中,具有n个关键字的节点只含有n棵子树,即每个关键字对应一颗子树;而在B树中,具有n个关键字的节点有n+1棵子树
2)B+树:每个节点(非根节点)关键字个数【m/2】<=n<=m (根节点:1<=n<=m),
在B树:[m/2]-1<=n<=m-1(根节点:1<=n<=m-1)
3) 在B+树中,叶节点包含信息,所有非叶节点仅起到索引作用,非叶节点中的每个索引项只含有对应子树的最大关键字和指向孩子树的指针,不含有该关键字对应记录的存储地址。
4) 在B+树中,叶节点包含了全部关键字,即在非叶节点中出现的关键字也会出现在叶节点中。而在B树中,叶节点包含的关键字和其它节点包含的关键字是不重复的。
B+树有一个最大的好处,方便扫库,B树必须用中序遍历的方法按序扫库,而B+树直接从叶子结点挨个扫一遍就完了。
B+树支持range-query(区间查询)非常方便,而B树不支持。这是数据库选用B+树的最主要原因。
通常在B+树中,有两个头指针,一个指向根节点,另一个指向关键字最小的叶节点。因此,B+树可以进行两种查找:一种是从最小关键字开始的顺序查找,另一种是从根节点开始,进行多路查找。
B树,又称为多路平衡查找树,B树中所有节点的孩子节点数的最大值称为B树的阶,通常用m表示,一颗m阶B树或为空树,或为满足如下特性的m叉树:
1)书中每个节点之多有m棵子树(即至多含有m-1个关键字)
2)若根节点不是终端节点,则至少有两颗子树,(至少含有一个关键字)
3)除根节点外的所有非叶节点至少有取上界【m/2】棵子树(即至少含有【m/2】-1个关键字)
4)n为关键字的个数,则【m/2】-1<=n<=m-1
| P0 | K0 | P1 | K1 | P2 | K2 | P3 |

1、B树的高度
1)一棵树包含n个关键字、高度为h、阶数为m的B树:
因为B树种每个节点最多有m-1个关键字,所以在一颗高度为h的m阶B树种关键字的个数应该满足:
n<=(m-1)*(1+m+m^2 +h-1))=m^h-1
h>=logm(n+1)
2)若让每个节点中的关键字个数达到最少,则容纳同样多关键字的B树的高度可到达最大,由B树定义:第一层至少有1个节点,第二层至少有2个节点,除根节点以外的每个非终端几点至少有【m/2】棵子树,则第三层至少有2【m/2】个节点。。。。第h+1层至少有2(【m/2】)(h-1)个节点,注意到第h+1层是不包含任何信息的叶节点。对关键字个数为n的B数,叶节点即查找不成功的节点为n+1,由此n+1>=2([m/2])(h-1),即h<=logm/2+1
2、B树的查找
在B树上进行查找与二叉查找树很相似,只是每个节点都是多个节点关键字的有序表,在每个节点上所做的不是两路分支决定,而是根据该节点的子树所做的多路分支决定。
B树查找包含两个基本操作:1)在B树中找节点2)在结点内找关键字。由于B树常存储在磁盘上,则前一个查找操作是在磁盘上进行的,而后一个查找操作是在内存中进行的,即在找到目标节点后,先将节点中的信息读入内存,然后在采用顺序表查找法或折半查找法查找等于K的关键字。
3、B插入
1)定位:利用前述的B树查找算法,找出插入该关键字的最底层中某个非叶节点(注意,B树中的插入关键字一定是插入在最底层中某个非叶节点内)
2)插入:在B树中,每个非失败节点的关键字个数都在【[m/2]-1,m-1】之间,当插入后的节点关键字个数小于m,则可以直接插入;插入后检查被插入节点内关键字的个数,当插入后的节点关键字个数大于m-1时,则必须对节点进行分裂。
分裂的方法:取一个新节点,将插入key后的元原来从中间位置将其中的关键字分为两部分,左部分包含的关键字放在原节点中,有部分包含的关键字放到新节点中,中间位置【m/2】的节点插入到原节点的父节点中。若此时导致其父节点的关键字个数也超过了上限,则继续进行这种分裂操作,直至这个过程传到根节点为止,这样导致B树高度增1.

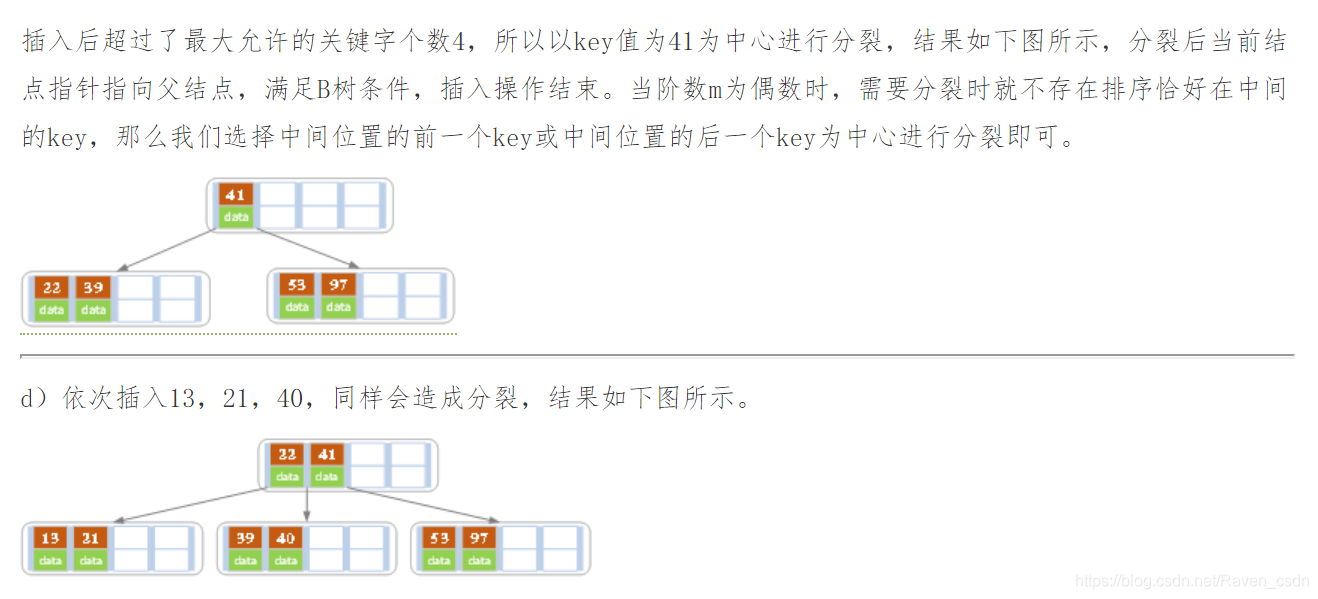



4、B树的删除
B树的删除和插入类似,需要涉及到合并问题。





B+树基本概念
B+树是应数据库所需而出现的一种B树的变形树。
一颗m阶B+树需要满足下列条件:
1)每个分支节点最多有m棵子树(子节点)
2)非叶根节点至少有两颗子树,其他每个分支节点至少有【m/2】棵子树
3)节点的子树个数与关键字个数相等
4)所有叶节点包含全部关键字及指向相应记录的指针,而且业绩点中将关键字按大小顺序排列,并且相邻叶节点按大小顺序互相连接起来。
5)所有分支节点中仅包含它的各个子节点中关键字的最大值以及指向其子节点的指针。
插入:
1)若为空树,创建一个叶子结点,然后将记录插入其中,此时这个叶子结点也是根结点,插入操作结束。
2)针对叶子类型结点:根据key值找到叶子结点,向这个叶子结点插入记录。插入后,若当前结点key的个数小于等于m-1,则插入结束。否则将这个叶子结点分裂成左右两个叶子结点,左叶子结点包含前m/2个记录,右结点包含剩下的记录,将第m/2+1个记录的key进位到父结点中(父结点一定是索引类型结点),进位到父结点的key左孩子指针向左结点,右孩子指针向右结点。将当前结点的指针指向父结点,然后执行第3步。
3)针对索引类型结点:若当前结点key的个数小于等于m-1,则插入结束。否则,将这个索引类型结点分裂成两个索引结点,左索引结点包含前(m-1)/2个key,右结点包含m-(m-1)/2个key,将第m/2个key进位到父结点中,进位到父结点的key左孩子指向左结点, 进位到父结点的key右孩子指向右结点。将当前结点的指针指向父结点,然后重复第3步。






B+树的删除操作
如果叶子结点中没有相应的key,则删除失败。否则执行下面的步骤
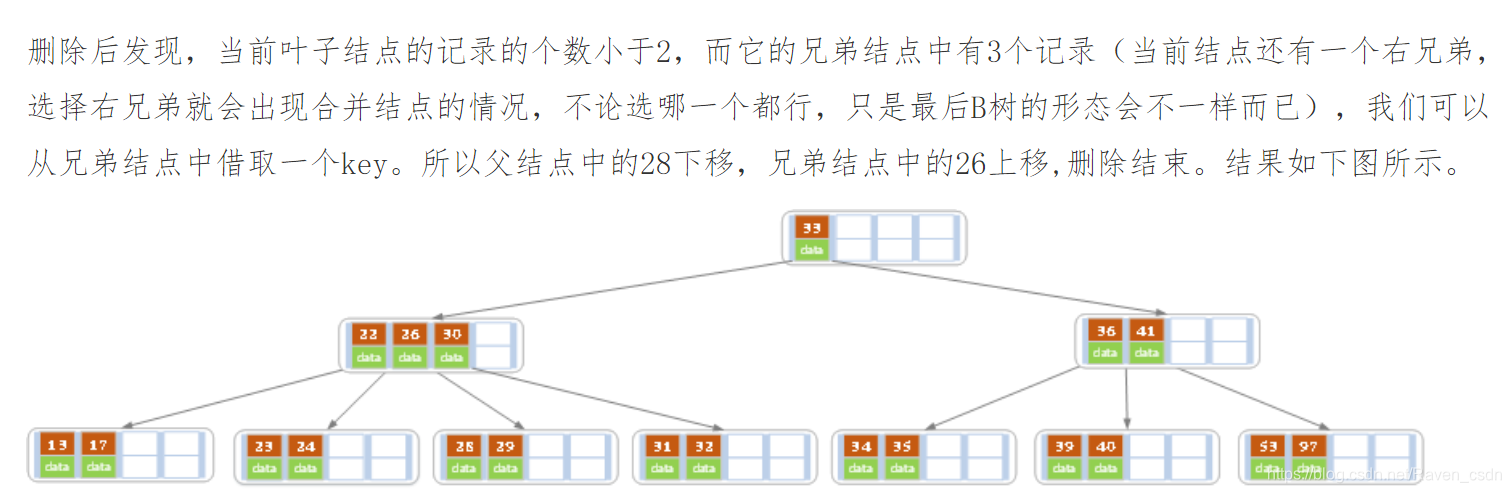
1)删除叶子结点中对应的key。删除后若结点的key的个数大于等于Math.ceil(m-1)/2 – 1,删除操作结束,否则执行第2步。
2)若兄弟结点key有富余(大于Math.ceil(m-1)/2 – 1),向兄弟结点借一个记录,同时用借到的key替换父结(指当前结点和兄弟结点共同的父结点)点中的key,删除结束。否则执行第3步。
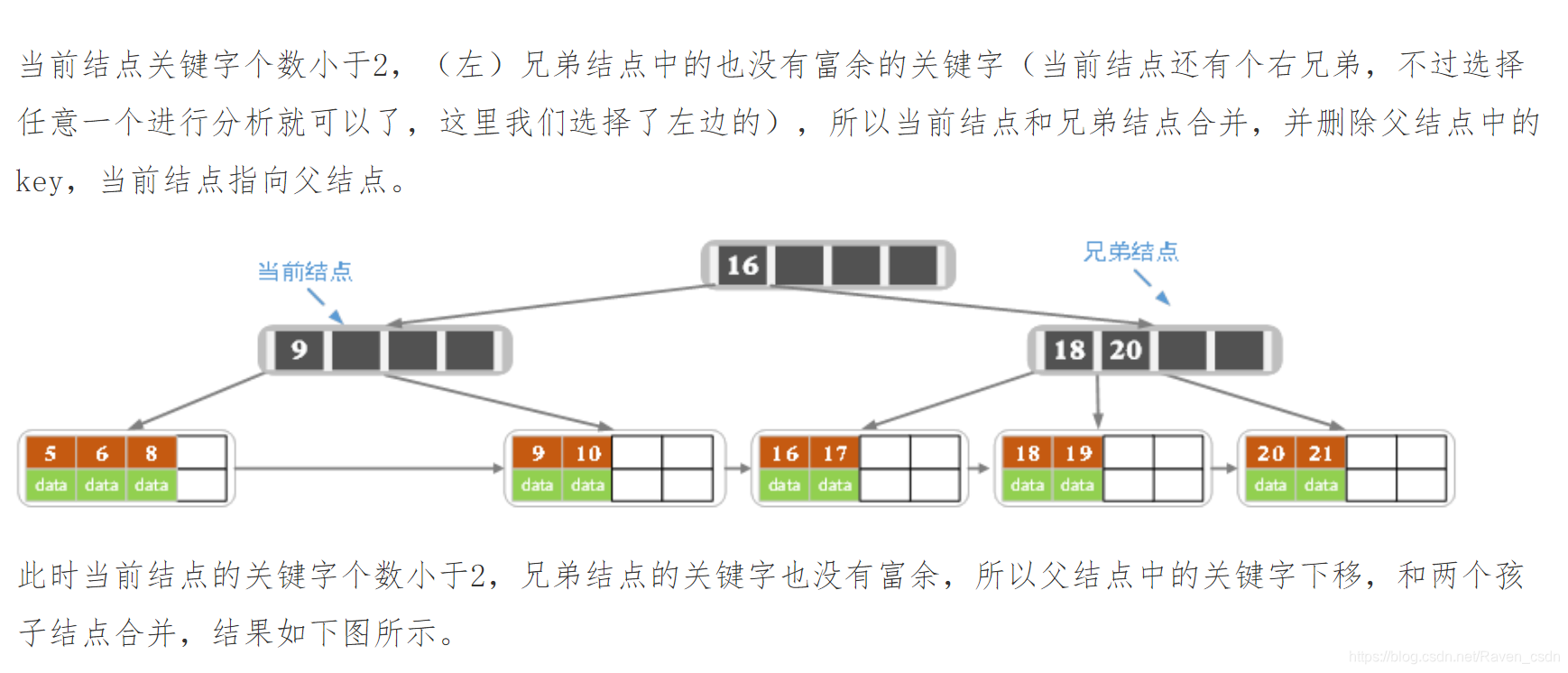
3)若兄弟结点中没有富余的key,则当前结点和兄弟结点合并成一个新的叶子结点,并删除父结点中的key(父结点中的这个key两边的孩子指针就变成了一个指针,正好指向这个新的叶子结点),将当前结点指向父结点(必为索引结点),执行第4步(第4步以后的操作和B树就完全一样了,主要是为了更新索引结点)。
4)若索引结点的key的个数大于等于Math.ceil(m-1)/2 – 1,则删除操作结束。否则执行第5步
5)若兄弟结点有富余,父结点key下移,兄弟结点key上移,删除结束。否则执行第6步
6)当前结点和兄弟结点及父结点下移key合并成一个新的结点。将当前结点指向父结点,重复第4步。
注意,通过B+树的删除操作后,索引结点中存在的key,不一定在叶子结点中存在对应的记录。
下面是一颗5阶B树的删除过程,5阶B数的结点最少2个key,最多4个key。









 本文详细介绍了B树和B+树的区别,包括它们的结构特性、查找、插入和删除操作。B+树相比B树更适用于数据库,支持范围查询且便于数据扫描。B树在查找时涉及磁盘I/O,而B+树所有数据都在叶子节点,适合批量读取。
本文详细介绍了B树和B+树的区别,包括它们的结构特性、查找、插入和删除操作。B+树相比B树更适用于数据库,支持范围查询且便于数据扫描。B树在查找时涉及磁盘I/O,而B+树所有数据都在叶子节点,适合批量读取。
















 2187
2187

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








