多目标灰狼优化算法-MOGWO-（多目标天线设计优化/无线电频谱分配/智能交通信号控制优化）

 MOGWO（Multi-Objective Grey Wolf Optimizer）是一种基于灰狼优化算法（Grey Wolf Optimizer, GWO）的多目标优化算法。以下是关于 MOGWO 的详细介绍：

 具体算法信息请跳转：多目标灰狼优化算法-MOGWO-（多目标天线设计优化/无线电频谱分配/智能交通信号控制优化）

基本原理

• 灰狼优化算法：GWO 是一种模拟灰狼群体狩猎行为的启发式算法。在 GWO 中，灰狼群体被分为四个等级：α、β、δ 和 ω 狼。α 狼是最优解，β 狼是次优解，δ 狼是第三优解，ω 狼是其余的狼。狼群在搜索空间中通过更新位置来寻找猎物（最优解），位置更新公式如下：
• 多目标扩展：MOGWO 将 GWO 扩展到多目标优化问题，主要通过以下几个方面：
  • Pareto 最优性：在多目标优化中，不存在单一的最优解，而是一个 Pareto 最优解集。因此，MOGWO 需要考虑如何在更新狼群位置时维护和更新 Pareto 最优解集。
  • 领导者选择：在 MOGWO 中，α、β、δ 狼不是单一的最优个体，而是从 Pareto 最优解集中选择多个非支配解作为领导者。这些领导者引导狼群向不同的非支配区域搜索。

• 关键步骤

• 种群初始化：
  • 随机生成一定数量的灰狼个体，每个个体代表一个潜在的解，其位置表示决策变量的值。
  • 初始化时，将每个个体的位置设置在搜索空间内，搜索空间由决策变量的上下限决定。
• 评估个体：
  • 使用目标函数对每个个体进行评估，计算其适应度值。对于多目标问题，会得到多个适应度值（每个目标一个）。
  • 确定初始的 Pareto 最优解集，将非支配个体添加到 Pareto 最优解集中。
• 更新系数：
  • 根据迭代次数更新系数和，引导狼群从探索阶段（较大时）向开发阶段（较小时）转变。
• 领导者选择：
  • 从 Pareto 最优解集中选择多个个体作为 α、β、δ 狼。
  • 选择方式可以是随机选择，也可以根据某种策略，如优先选择多样性高的个体。
• 位置更新：
  • 对于每个 ω 狼（其余个体），根据 α、β、δ 狼的位置更新自己的位置。通常会根据不同的位置更新公式更新，以平衡全局搜索和局部搜索能力。
  • 位置更新公式一般基于 GWO 的公式，但会考虑多目标的情况，例如：

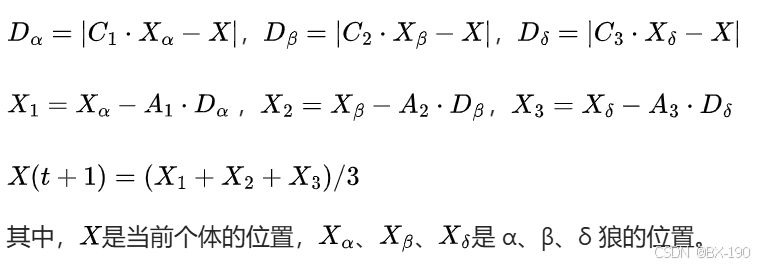
特点

• 简单高效：继承了 GWO 的简单结构，易于实现和理解，计算复杂度相对较低。
• 全局搜索能力：在算法开始时，具有较强的全局搜索能力，能够在搜索空间中广泛探索，寻找潜在的最优区域。
• 多样性维护：通过合适的 Pareto 最优解集维护策略，可以在一定程度上保持种群的多样性，找到分布较好的 Pareto 最优解。

应用场景

• 工程优化：在多目标的工程设计问题中，如结构设计中同时考虑重量和强度，或电子电路设计中同时考虑功耗和性能等。
• 资源分配：在网络资源分配中，需要同时考虑多个指标，如最大