多目标优化算法之灰狼优化算法(MOGWO)

多目标优化算法的最终目标是找到具有最高多样性的真实帕累托最优解的非常精确的近似。这使得决策者可以有多样化的设计方案。

多目标灰狼算法MOGWO，代码写的很清楚，建议新手可以从这篇代码学起。

为了将 GWO 用于多目标优化，代码中集成了两个新组件。采用的组件与MOPSO（Coello 等人，2004）的组件非常相似。其一是存档，负责存储到目前为止获得的非支配性帕累托最优解。其二是一个领导者选择策略，协助选择 alpha、beta 和 delta 的解，作为从存档中获得的狩猎过程的领导者。

MOGWO 算法的伪代码如下：

MOGWO 的源代码在http://www.alimirjalili.com/GWO.html 上公开提供。

MOGWO 算法的收敛性是有保证的，因为它利用了相同的数学模型来搜索最优解。事实证明，GWO 要求搜索智能体在优化的初期突然改变位置，在优化的后期逐渐改变位置。MOGWO算法继承了 GWO 的所有特征，这意味着搜索智能体以相同的方式探索和开发搜索空间。主要的区别是，MOGWO 围绕一组存档个体进行搜索（即使存档没有变化，也可能不同），而 GWO 只保存和改进三个最好的解。

MOGWO采用的是网格机制，想要非支配排序机制的多目标优化算法的小伙伴，可以关注多目标猫群优化和多目标鲸鱼优化，后续会陆续发布。

MOGWO在CEC2009多目标函数ZDT3上的表现如下图所示：

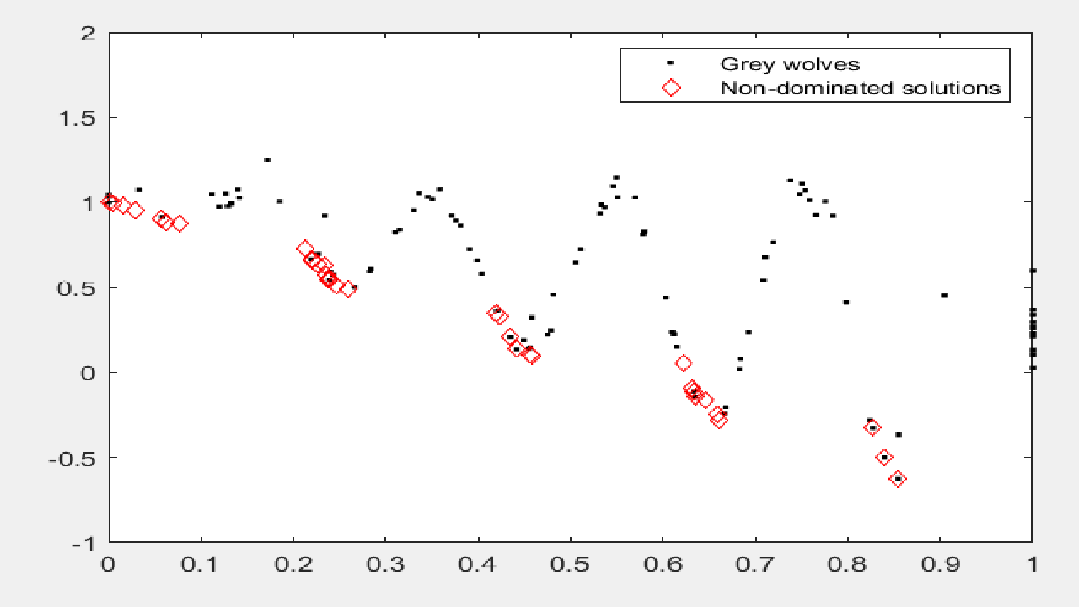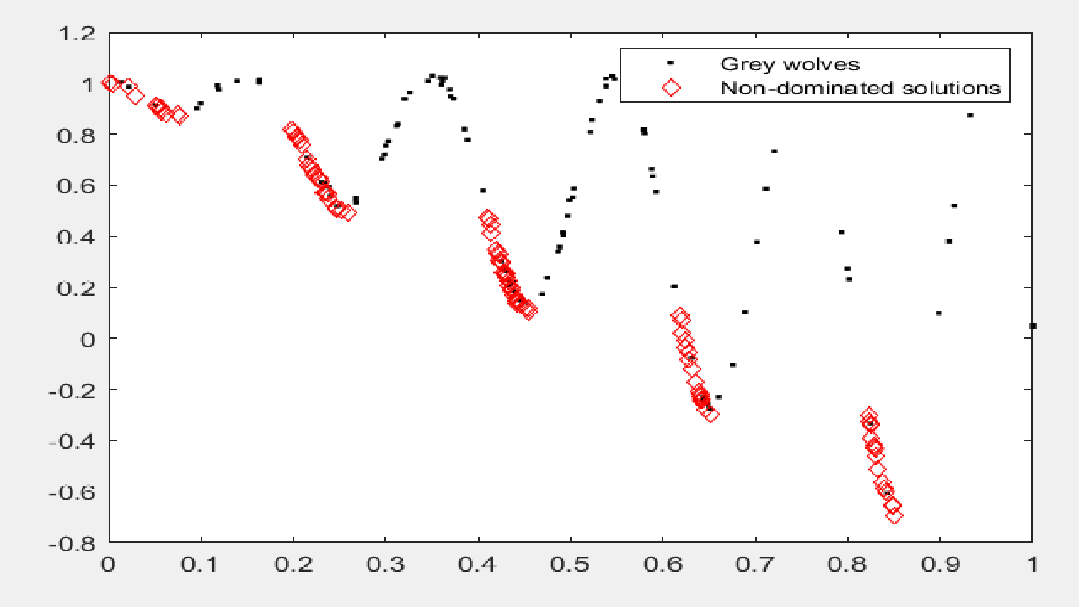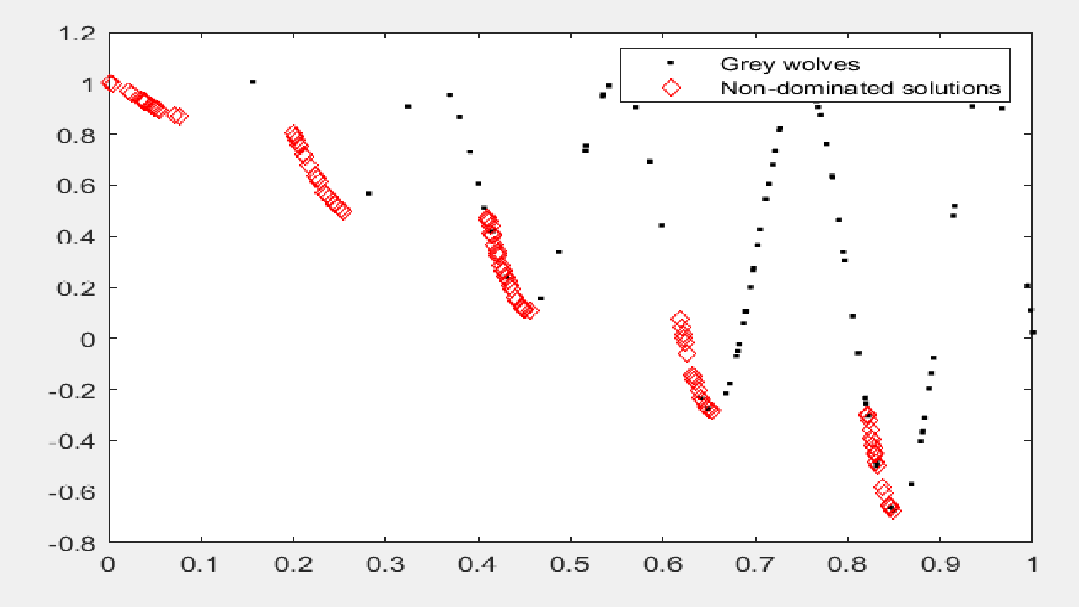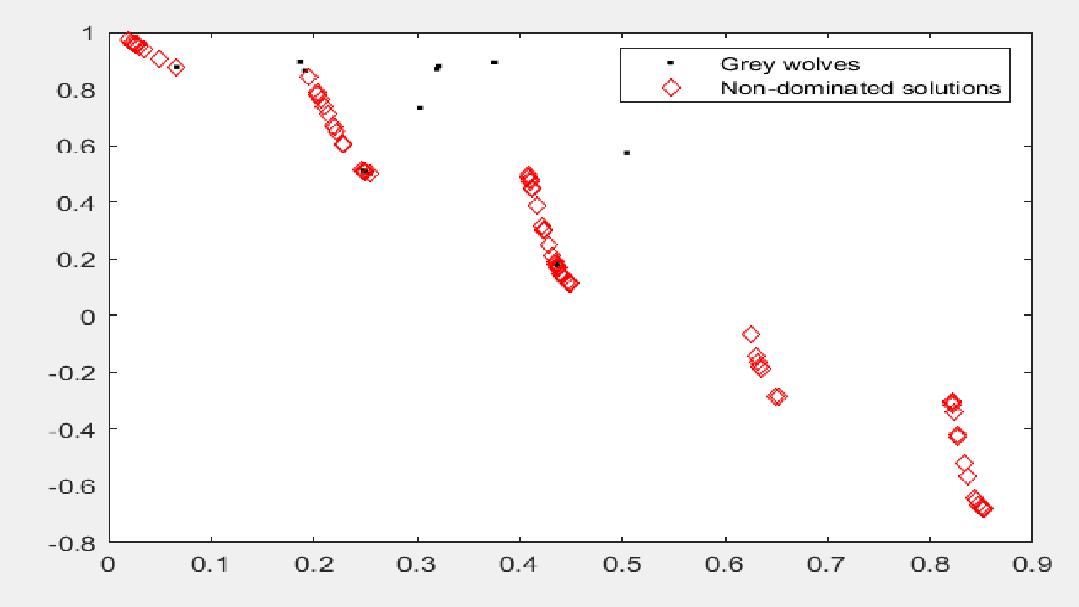
代码：

clear all
clc
drawing_flag = 1;
nVar=5;
fobj=@(x) ZDT3(x);
% Lower bound and upper bound
lb=zeros(1,5);
ub=ones(1,5);
VarSize=[1 nVar];
GreyWolves_num=100;
MaxIt=50;  % Maximum Number of Iterations
Archive_size=100;   % Repository Size


alpha=0.1;  % Grid Inflation Parameter
nGrid=10;   % Number of Grids per each Dimension
beta=4; %=4;    % Leader Selection Pressure Parameter
gamma=2;    % Extra (to be deleted) Repository Member Selection Pressure
% Initialization
GreyWolves=CreateEmptyParticle(GreyWolves_num);
for i=1:GreyWolves_num
    GreyWolves(i).Velocity=0;
    GreyWolves(i).Position=zeros(1,nVar);
    for j=1:nVar
        GreyWolves(i).Position(1,j)=unifrnd(lb(j),ub(j),1);
    end
    GreyWolves(i).Cost=fobj(GreyWolves(i).Position')';
    GreyWolves(i).Best.Position=GreyWolves(i).Position;
    GreyWolves(i).Best.Cost=GreyWolves(i).Cost;
end


GreyWolves=DetermineDomination(GreyWolves);


Archive=GetNonDominatedParticles(GreyWolves);


Archive_costs=GetCosts(Archive);
G=CreateHypercubes(Archive_costs,nGrid,alpha);


for i=1:numel(Archive)
    [Archive(i).GridIndex Archive(i).GridSubIndex]=GetGridIndex(Archive(i),G);
end


% MOGWO main loop


for it=1:MaxIt
    a=2-it*((2)/MaxIt);
    for i=1:GreyWolves_num
        
        clear rep2
        clear rep3
        
        % Choose the alpha, beta, and delta grey wolves
        Delta=SelectLeader(Archive,beta);
        Beta=SelectLeader(Archive,beta);
        Alpha=SelectLeader(Archive,beta);
        
        % If there are less than three solutions in the least crowded
        % hypercube, the second least crowded hypercube is also found
        % to choose other leaders from.
        if size(Archive,1)>1
            counter=0;
            for newi=1:size(Archive,1)
                if sum(Delta.Position~=Archive(newi).Position)~=0
                    counter=counter+1;
                    rep2(counter,1)=Archive(newi);
                end
            end
            Beta=SelectLeader(rep2,beta);
        end
        
        % This scenario is the same if the second least crowded hypercube
        % has one solution, so the delta leader should be chosen from the
        % third least crowded hypercube.
        if size(Archive,1)>2
            counter=0;
            for newi=1:size(rep2,1)
                if sum(Beta.Position~=rep2(newi).Position)~=0
                    counter=counter+1;
                    rep3(counter,1)=rep2(newi);
                end
            end
            Alpha=SelectLeader(rep3,beta);
        end
        
        % Eq.(3.4) in the paper
        c=2.*rand(1, nVar);
        % Eq.(3.1) in the paper
        D=abs(c.*Delta.Position-GreyWolves(i).Position);
        % Eq.(3.3) in the paper
        A=2.*a.*rand(1, nVar)-a;
        % Eq.(3.8) in the paper
        X1=Delta.Position-A.*abs(D);
        
        
        % Eq.(3.4) in the paper
        c=2.*rand(1, nVar);
        % Eq.(3.1) in the paper
        D=abs(c.*Beta.Position-GreyWolves(i).Position);
        % Eq.(3.3) in the paper
        A=2.*a.*rand()-a;
        % Eq.(3.9) in the paper
        X2=Beta.Position-A.*abs(D);
        
        
        % Eq.(3.4) in the paper
        c=2.*rand(1, nVar);
        % Eq.(3.1) in the paper
        D=abs(c.*Alpha.Position-GreyWolves(i).Position);
        % Eq.(3.3) in the paper
        A=2.*a.*rand()-a;
        % Eq.(3.10) in the paper
        X3=Alpha.Position-A.*abs(D);
        
        % Eq.(3.11) in the paper
        GreyWolves(i).Position=(X1+X2+X3)./3;
        
        % Boundary checking
        GreyWolves(i).Position=min(max(GreyWolves(i).Position,lb),ub);
        
        GreyWolves(i).Cost=fobj(GreyWolves(i).Position')';
    end
    
    GreyWolves=DetermineDomination(GreyWolves);
    non_dominated_wolves=GetNonDominatedParticles(GreyWolves);
    
    Archive=[Archive
        non_dominated_wolves];
    
    Archive=DetermineDomination(Archive);
    Archive=GetNonDominatedParticles(Archive);
    
    for i=1:numel(Archive)
        [Archive(i).GridIndex Archive(i).GridSubIndex]=GetGridIndex(Archive(i),G);
    end
    
    if numel(Archive)>Archive_size
        EXTRA=numel(Archive)-Archive_size;
        Archive=DeleteFromRep(Archive,EXTRA,gamma);
        
        Archive_costs=GetCosts(Archive);
        G=CreateHypercubes(Archive_costs,nGrid,alpha);
        
    end
    
    disp(['In iteration ' num2str(it) ': Number of solutions in the archive = ' num2str(numel(Archive))]);
    save results
    
    % Results
    
    costs=GetCosts(GreyWolves);
    Archive_costs=GetCosts(Archive);
    
    if drawing_flag==1
        hold off
        plot(costs(1,:),costs(2,:),'k.');
        hold on
        plot(Archive_costs(1,:),Archive_costs(2,:),'rd');
        legend('Grey wolves','Non-dominated solutions');
        drawnow
    end  
end

免费完整代码获取，后台回复关键词：

多目标02