64.买卖股票的最佳时机

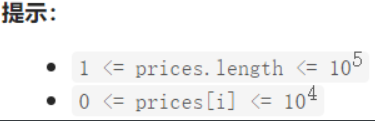
一、题目描述

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

二、解题思路

先来简单分析一下，如果我今天买入了一支股票，到了明天我想知道此时我手上的股票的利润有多少，就需要用明天股票的价值减去昨天买入的时候的价值，到了后天也是，仍需要减去买入时候的价值才知道赔了还是赚了。

第一步：确定dp数组（dp table）以及下标的含义

这里需要用一个二维数组来表示，dp[i][j]，它表示第i天结束的时候持有股票的状态是j时，此时手上的现金数（这个现金数指的是卖出那天股票的价值减去买入股票时的价值）。这里为什么说是状态呢？假如在第i天之前你手上有股票，说明你在第i天前的某一天是买入了股票的。如果在这之前你没有持有股票说明你的状态是和前一天是一样的，都是没有持股的状态，那么用0和1来表示这两种状态。

• 当j=0，表示不持股，dp[i][0]表示第i天这一天结束不持股的转态下（一定要明确是持有股票，不代表这一天要买股票）此时手上的价值。此时有两种可能性：
  1. 第i天不持有股票，那么i-1天也不持有股票。表示：dp[i-1][0]
  2. 第i-1天持有股票，在第i天卖出了，此时手上也是一个未持股的状态，但是手上的价值变了，因为买卖的股票。表示：dp[i-1][1]+price[i]
• 当j=1，表示持股，dp[i][1]表示第i天持股状态下的价值，此时也是有两中可能性：
  1. 在i-1（前一天）天不持股，但是在今天（i这一天买入了股票），此时手上的价值要注意是第i这一天股票的价值的相反数，因为你是买入了股票花了你自己的钱，并不是赚的。表示：-price[i]
  2. 在i-1天就持股了，今天不做任何事情也就是不卖，那么今天的状态还是一个持股状态。表示：dp[i-1][1]

第二步：确定递推公式

不管是在第i天持有股票还是不持有股票，在这一天的价值都是选两种可能性中最大的，这毋庸置疑。

dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1]+prices[i])
dp[i][1] = Math.max(dp[i-1][1], -prices[i])

第三步：dp数组如何初始化

初始状态dp[0][0]=0，不持股价值肯定是0；dp[0][1]=-prices[0]买入的这一天价值就是股票价值的相反数，因为花钱买了股票。

第四步：确定遍历顺序

正常的从前向后遍历就行，后一天的状态都是从前一天转移过来的。

for(int i=1; i<prices.length; i++){
    dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1]+prices[i]);
    dp[i][1] = Math.max(dp[i-1][1], -prices[i]);
}

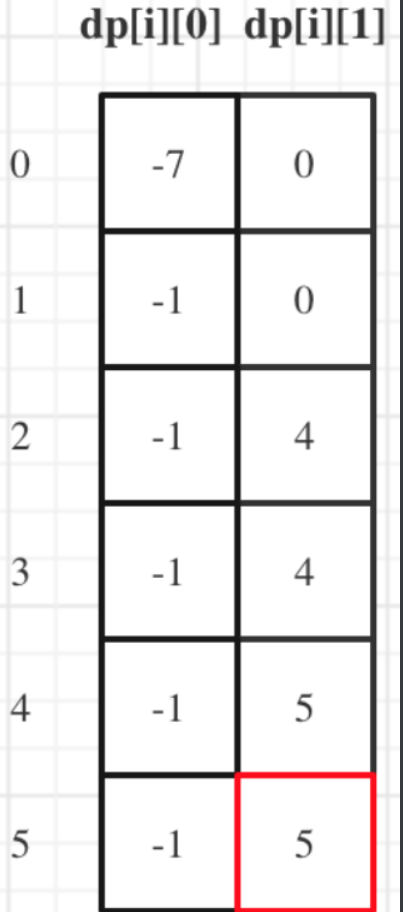
第五步：举例推导dp数组

以示例1，输⼊：[7,1,5,3,6,4]为例，dp数组状态如下：

三、代码演示

class Solution {
    public int maxProfit(int[] prices) {
        //特判：如果数组中只有一天的股票价值，那么没有利润
        if(prices.length<2){
            return 0;
        }

        //声明dp
        int[][] dp = new int[prices.length][2];

        //dp初始化
        dp[0][0] = 0;
        dp[0][1] = -prices[0];

        //遍历
        for(int i=1; i<prices.length; i++){
            dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1]+prices[i]);
            dp[i][1] = Math.max(dp[i-1][1], -prices[i]);
        }
        //返回的肯定是不持股的状态，因为卖出了你才能获取利润
        return dp[prices.length-1][0];

    }
}

• 时间复杂度：O(N)，遍历股价数组可以得到最优解；
• 空间复杂度：O(N)，状态数组的长度为 N*。