48.不同的二叉搜索树

一、题目描述

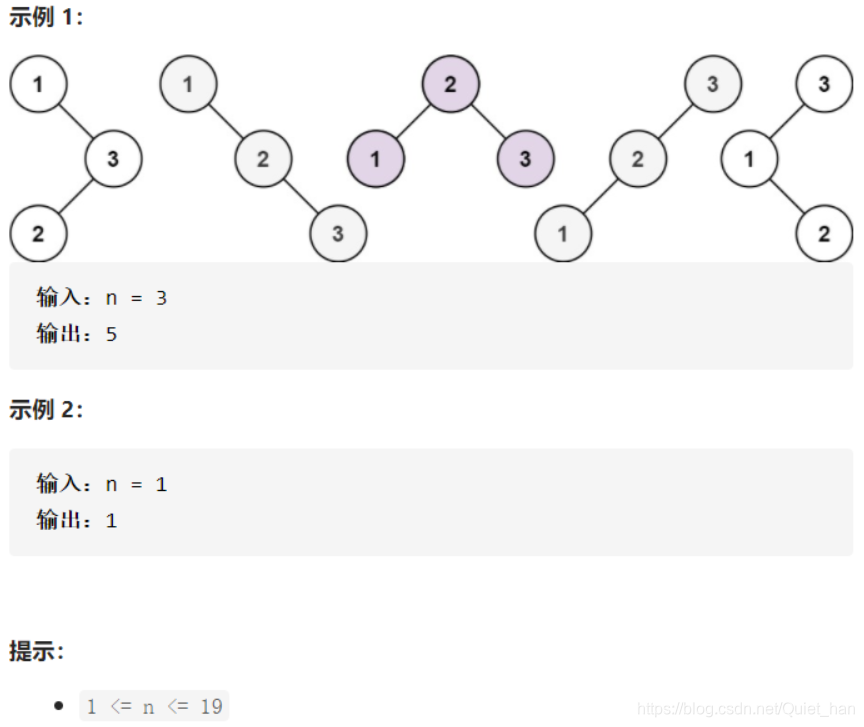
给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

二、解题思路

不知道二叉搜索树可以先看47_验证二叉搜索树这道题，刚开始看一眼本题目是没有任何思路的，也是通过看了一些大佬的分析，这里也来总结一下。

先来举几个例子，看是不是有什么规律呢？

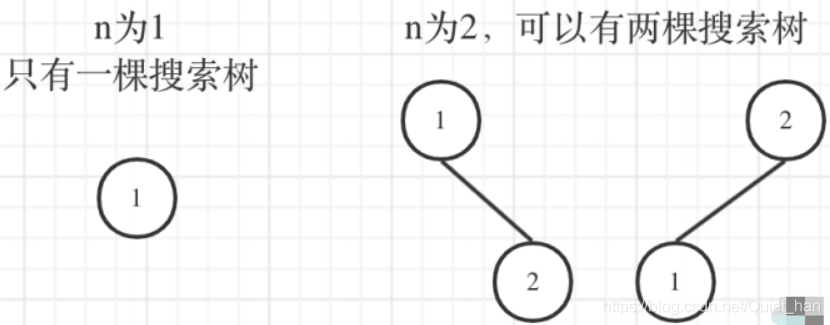
通过上图可以看到，当n=1时，所得二叉搜索树是一颗，当n=2时，可以得到两颗二叉搜索树。继续来看n=3的时候：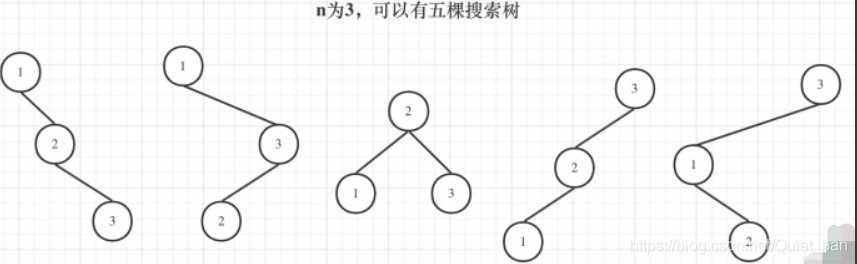
可以看到能得到5颗子树，那么来分析一下这五颗子树的组成，看是不是有什么规律呢？

首先，五颗子树的头结点分别有1, 2, 3 组成：

当1为头结点时，子树全部分布在右子树，并且可以发现分布结构和n=2时是一样的。

当2为头结点时，求左右子树都为一个节点，我们可以把左右子树当做n=1时的分布。

分析到这里，就可以看到重叠子问题了。

当头结点为3的时候，我们可以总结到：元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量 ，这个式子的总和就是头结点为3时的二叉搜索树的数量。那下面来看看这个式子中的三个变量该如何通过计算得到呢？

元素1为头结点搜索树的数量 = 右⼦树有2个元素的搜索树数量 * 左⼦树有0个元素的搜索树数量

元素2为头结点搜索树的数量 = 右⼦树有1个元素的搜索树数量 * 左⼦树有1个元素的搜索树数量

元素3为头结点搜索树的数量 = 右⼦树有0个元素的搜索树数量 * 左⼦树有2个元素的搜索树数量

有2个元素的搜索树数量就是dp[2]。

有1个元素的搜索树数量就是dp[1]。

有0个元素的搜索树数量就是dp[0]。

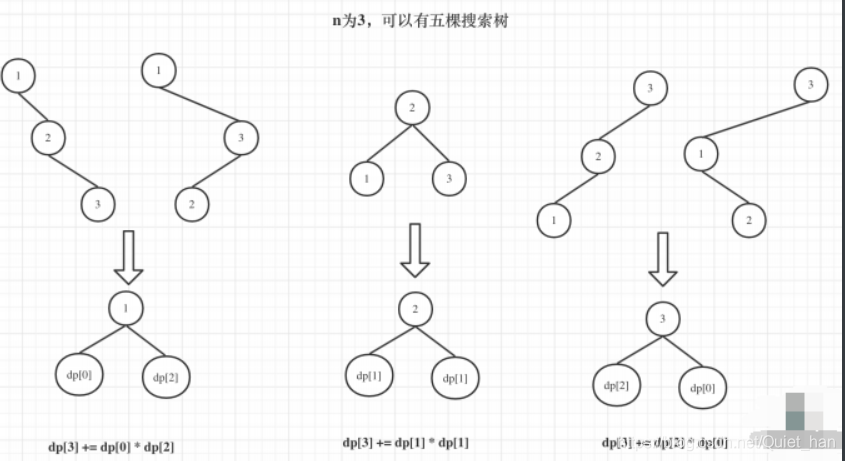
所以就可得到：dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]

如下图：

然后利用动规五部曲：

第一步：确定dp数组（dp table）以及下标的含义

dp[i] ：1到i为节点组成的⼆叉搜索树的个数为dp[i]。

也可以理解是i的不同元素节点组成的⼆叉搜索树的个数为dp[i] ，都是⼀样的。

第二步：确定转态转移方程（递推公式）

在上⾯的分析中，其实已经看出其递推关系， dp[i] += dp[以j为头结点左⼦树节点数量] * dp[以j为头结

点右⼦树节点数量]

j相当于是头结点的元素，从1遍历到i为⽌。所以：

dp[i] += dp[j - 1] * dp[i - j];

-1 为j为头结点左⼦树节点数量，i-j 为以j为头结点右⼦树节点数量

第三步：dp数组初始化

初始化，只需要初始化dp[0]就可以了，推导的基础，都是dp[0]。那么dp[0]应该是多少呢？

从定义上来讲，空节点也是⼀颗⼆叉树，也是⼀颗⼆叉搜索树，这是可以说得通的。

从递归公式上来讲，dp[以j为头结点左⼦树节点数量] * dp[以j为头结点右⼦树节点数量] 中以j为头结点

左⼦树节点数量为0，需要dp[以j为头结点左⼦树节点数量] = 1， 否则乘法的结果就都变成0了。

所以初始化dp[0] = 1

第四步：确定遍历顺序

⾸先⼀定是遍历节点数，从递归公式：dp[i] += dp[j - 1] * dp[i - j]可以看出，节点数为i的状态是依靠 i之

前节点数的状态。那么遍历i⾥⾯每⼀个数作为头结点的状态，⽤j来遍历。

代码如下：

for(int i=1; i<=n; i++){
    for(int j=1; j<=i; j++){
        dp[i] += dp[j-1] + dp[i-j]
    }
}

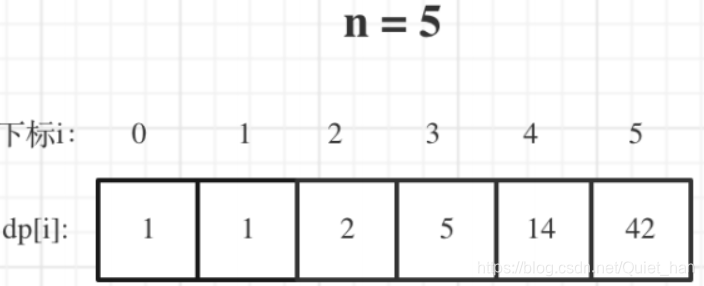
第五步：举例推导dp数组

当n=5时的数组转态：

三、代码演示

class Solution {
    public int numTrees(int n) {
        //用来存放结果的dp数组
        int[] dp = new int[n+1];
		//初始化dp数组
        dp[0] = 1;
		//确定遍历顺序
        for(int i=1; i<=n; i++){
            for(int j=1; j<=i; j++){
                //转态转移方程
                dp[i] = dp[i] + dp[j-1]*dp[i-j];
            }
        }
        return dp[n];
    }
}