理解GRPO，超越GRPO！GVPO算法详解

作者：张凯成
原文：https://zhuanlan.zhihu.com/p/1911487456173359632

TL;DR

我们提出了GVPO，优势:(1)唯一最优解恰好是KL约束的reward最大化最优解(2)支持多样化采样分布，避免on-policy和重要性采样带来的各种问题。

随着Deepseek的火爆，其中用到的强化学习算法GRPO也引起了广泛关注。GRPO通过对每一个prompt多次采样，避免了额外训练value model的开销。尽管如此，实践中复现GRPO经常表现出训练不稳定、效果表现不佳等症状。为此我们提出了GVPO(Group Variance Policy Optimization), 可以无缝适配现有GRPO框架并取得更好的表现、更稳定的训练并支持更丰富的数据来源。

动机

受到DPO的启发，我们也希望在GRPO场景(每个prompt多次采样)下利用KL约束的reward最大化

$$ma{x}_{{\pi }_{\theta }}{\mathbb{E}}_{x\sim \mathcal{D},y\sim {\pi }_{\theta }(y|x)}[R(x,y)]-\beta {\mathbb{D}}_{KL}[{\pi }_{\theta }(y|x)||{\pi }_{{\theta }^{\prime }}(y|x)]$$

的解析解形式：

$$R_{\theta }(x,y)=\beta \log \frac{{\pi }_{\theta }(y|x)}{{\pi }_{{\theta }^{\prime }}(y|x)}+\beta \log Z(x)$$

然而这里有一个问题在于公式里的Z(x)是对所有可能y的期望，在实践中难以计算。为此，我们发现当一个prompt内所有采样的梯度系数加和为0时，Z(x)可以被消掉。

即对于

$${\nabla }_{\theta }\mathcal{L}(\theta )=-\sum _{(x,y_1,y_2,..,y_k)\in \mathcal{D}}\sum _{i=1}^k{w}_i{\nabla }_{\theta }\log {\pi }_{\theta }(y_i|x)$$

当

$$\sum _{i=1}^k{w}_i=0时有\sum _{i=1}^k{w}_i{R}_{\theta }(x,y)=\sum _{i=1}^k{w}_i\beta \log \frac{{\pi }_{\theta }(y|x)}{{\pi }_{{\theta }^{\prime }}(y|x)}$$

GVPO

受此启发，我们提出了GVPO：

$${\nabla }_{\theta }{\mathcal{L}}_{\text{GVPO}}(\theta )$$
=−β∑(x,{yi})∈D∑i=1k[(R(x,yi)−R(x,{yi}‾)−β(log⁡πθ(yi∣x)πθ′(yi∣x)−log⁡πθ({yi}∣x)πθ′({yi}∣x)‾)]∇θlog⁡πθ(yi∣x) =-\beta\sum_{(x, \{y_i\}) \in \mathcal{D}} \sum_{i=1}^k [(R(x,y_i)-\overline{R(x,\{y_i\}})-\beta(\log\frac{\pi_\theta(y_i|x)}{\pi_{\theta^\prime}(y_i|x)} - \overline{\log\frac{\pi_\theta(\{y_i\}|x)}{\pi_{\theta^\prime}(\{y_i\}|x)}})] \nabla_\theta\log \pi_\theta(y_i|x) =−β(x,{yi​})∈D∑​i=1∑k​[(R(x,yi​)−R(x,{yi​}​)−β(logπθ′​(yi​∣x)πθ​(yi​∣x)​−logπθ′​({yi​}∣x)πθ​({yi​}∣x)​​)]∇θ​logπθ​(yi​∣x)

其中

R(x,{yi}‾)=1k∑i=1kR(x,yi),log⁡πθ({yi}∣x)πθ′({yi}∣x)‾=1k∑i=1klog⁡πθ(yi∣x)πθ′(yi∣x) \overline{R(x,\{y_i\}})=\frac{1}{k}\sum_{i=1}^k R(x,y_i),\overline{\log\frac{\pi_\theta(\{y_i\}|x)}{\pi_{\theta^\prime}(\{y_i\}|x)}}=\frac{1}{k}\sum_{i=1}^k\log\frac{\pi_\theta(y_i|x)}{\pi_{\theta^\prime}(y_i|x)} R(x,{yi​}​)=k1​i=1∑k​R(x,yi​),logπθ′​({yi​}∣x)πθ​({yi​}∣x)​​=k1​i=1∑k​logπθ′​(yi​∣x)πθ​(yi​∣x)​

我们证明GVPO具有非常好的物理性质。具体来说

$${\nabla }_{\theta }{\mathcal{L}}_{\text{GVPO}}(\theta )$$
=−∑x,{yi}∑i=1k[(R(x,yi)−R(x,{yi}‾)−(Rθ(x,yi)−Rθ(x,{yi}‾)]∇θβlog⁡πθ(yi∣x) =-\sum_{x, \{y_i\}} \sum_{i=1}^k [(R(x,y_i)-\overline{R(x,\{y_i\}})-(R_\theta(x,y_i)-\overline{R_\theta(x,\{y_i\}})] \nabla_\theta \beta\log \pi_\theta(y_i|x) =−x,{yi​}∑​i=1∑k​[(R(x,yi​)−R(x,{yi​}​)−(Rθ​(x,yi​)−Rθ​(x,{yi​}​)]∇θ​βlogπθ​(yi​∣x)
=−∑x,{yi}∑i=1k[(R(x,yi)−R(x,{yi}‾)−(Rθ(x,yi)−Rθ(x,{yi}‾)]∇θ(Rθ(x,yi)−Rθ(x,{yi}‾) =-\sum_{x, \{y_i\} } \sum_{i=1}^k [(R(x,y_i)-\overline{R(x,\{y_i\}})-(R_\theta(x,y_i)-\overline{R_\theta(x,\{y_i\}})] \nabla_\theta(R_\theta(x,y_i)-\overline{R_\theta(x,\{y_i\}}) =−x,{yi​}∑​i=1∑k​[(R(x,yi​)−R(x,{yi​}​)−(Rθ​(x,yi​)−Rθ​(x,{yi​}​)]∇θ​(Rθ​(x,yi​)−Rθ​(x,{yi​}​)
=12∇θ∑x,{yi}∑i=1k[(Rθ(x,yi)−Rθ(x,{yi}‾)−(R(x,yi)−R(x,{yi}‾)]2 =\frac{1}{2}\nabla_\theta\sum_{x, \{y_i\} } \sum_{i=1}^k [(R_\theta(x,y_i)-\overline{R_\theta(x,\{y_i\}})-(R(x,y_i)-\overline{R(x,\{y_i\}})]^2 =21​∇θ​x,{yi​}∑​i=1∑k​[(Rθ​(x,yi​)−Rθ​(x,{yi​}​)−(R(x,yi​)−R(x,{yi​}​)]2

第一步是因为 $\beta \log Z(x)$ 可以被消掉。第二步是因为 ∑i=1kwi∇θR(x,{yi})‾=0\sum_{i=1}^k w_i \nabla_\theta \overline{R(x,\{y_i\})} =0∑i=1k​wi​∇θ​R(x,{yi​})​=0 。第三步是因为 ${\nabla }_{x}f(x{)}^2=2f(x){\nabla }_{x}f(x)$ 。

由此可见，GVPO居然本质是一个MSE loss！(喜）其中 (Rθ(x,yi)−Rθ(x,{yi}‾)(R_\theta(x,y_i)-\overline{R_\theta(x,\{y_i\}})(Rθ​(x,yi​)−Rθ​(x,{yi​}​) 是MSE的预测值， (R(x,yi)−R(x,{yi}‾)(R(x,y_i)-\overline{R(x,\{y_i\}})(R(x,yi​)−R(x,{yi​}​) 是MSE的真实值。

理论保证

基于这个变形，我们很容易（注意到.jpg）证明GVPO的理论最优解恰好是KL约束的reward最大化的最优解，即 $R_{\theta }=R,{\pi }_{\theta }={\pi }^{\ast }$ 。

定理1

最小化 ${\hat{\mathcal{L}}}_{\text{GVPO}}(\theta )$ 的唯一policy是 ${\pi }_{\theta }(y|x)={\pi }^{\ast }(y|x)=\frac{1}{Z(x)}{\pi }_{{\theta }^{\prime }}(y|x)e^{R(x,y)/\beta }$ ，其中

$${\hat{\mathcal{L}}}_{\text{GVPO}}(\theta )={\mathbb{E}}_{x\sim \mathcal{D}}{\mathbb{E}}_{y\sim {\pi }_{{\theta }^{\prime }}(\cdot |x)}[(R_{\theta }(x,y)-{\mathbb{E}}_{y\sim {\pi }_{{\theta }^{\prime }}}{R}_{\theta }(x,y))-(R(x,y)-{\mathbb{E}}_{y\sim {\pi }_{{\theta }^{\prime }}}R(x,y)){]}^2$$

这个定理保证了GVPO实践中的有效性和稳定性。

上式中 y 是依惯例从要对齐的policy ${\pi }_{{\theta }^{\prime }}$ 中采样，在实践中即 ${\pi }_{ref}或{\pi }_{{\theta }_{old}}$ 。我们接下来可以证明，GVPO支持从更广泛的分布中采样，且依然保持最优解性质。

定理2

最小化 ${\hat{\mathcal{L}}}_{\text{GVPO}}(\theta )$ 的唯一policy是 $\pi_\theta (y|x)=\pi^* (y|x)= \frac{1}{Z(x)}\pi_{\theta^{\prime}(y|x)e}{R(x,y)/\beta} $ ，其中

$${\hat{\mathcal{L}}}_{\text{GVPO}}(\theta )={\mathbb{E}}_{x\sim \mathcal{D}}{\mathbb{E}}_{y\sim {\pi }_s(\cdot |x)}[(R_{\theta }(x,y)-{\mathbb{E}}_{y\sim {\pi }_s}{R}_{\theta }(x,y))-(R(x,y)-{\mathbb{E}}_{y\sim {\pi }_s}R(x,y)){]}^2$$

对于满足 ${\pi }_s(y|x)>0$ 的任意 ${\pi }_s$ 都成立。

在实践中由softmax decoding的policy都满足这个定理的要求。这意味着，GVPO支持非常广泛的采样分布：

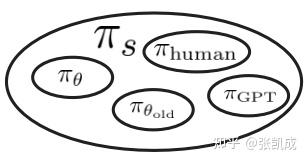
接下来我们正式展示GVPO的算法流程：

注意到GVPO的每个step中， ${\pi }_{\theta }$ 对齐的都是上一个step的policy ${\pi }_{{\theta }_{old}}$ 。我们还证明了，GVPO在n步结束后，依然能够对齐最初的policy:

定理3

使用 ${\hat{\mathcal{L}}}_{\text{GVPO}}({\theta }_t)$ 的n步算法——从 ${\pi }_{{\theta }_0}$ 开始，在第t步更新时设置 ${\pi }_{{\theta }^{\prime }}={\pi }_{{\theta }_{t-1}}$ ——最大化了如下目标

$${\mathbb{E}}_{x\sim \mathcal{D},y\sim {\pi }_{\theta }(y|x)}[R(x,y)]-\frac{\beta }{n}{\mathbb{D}}_{\text{KL}}[{\pi }_{\theta }(y|x)\Vert {\pi }_{{\theta }_0}(y|x)]$$

定理3可以保证GVPO的每一步更新都是稳定的（因为具有一个大约束 $\beta$ ），且最终优化可以“走得更远”（最终对齐的是 $\frac{\beta }{n}$ ）。

除此之外，文章中还证明了采样得到的loss是 ${\hat{\mathcal{L}}}_{\text{GVPO}}$ 的无偏一致估计量，进一步保证了算法的性能。

与DPO的比较

GVPO与DPO一样，都利用到了KL约束的reward最大化的解析解。DPO是利用BT模型，两两相减消去了不可计算的 Z(x) 。而GVPO则是利用了 ${\sum }_{i=1}^k{w}_i=0$ 的性质而适用于多response的情况。这两个算法利用解析解带来了两个好处：

• 保证了算法优化过程的稳定性， ${\pi }_{\theta }$ 不会过分偏离 ${\pi }_{ref}$
• 将一个同时有policy $\pi$ 和reward R 的复杂优化，简化成了只有reward R 和 $R_{\theta }$ 的简单优化。

除此之外，GVPO和DPO相比还有一个重要的理论优势。DPO其实不一定具有唯一的最优解，换句话说KL约束的reward最大化的解可能只是DPO众多最优解中的一个。这源于DPO依赖的BT模型的内生缺陷。这个问题会导致，优化DPO目标不一定会随之优化我们真实想要的目标（即KL约束的reward最大化）。而GVPO则由定理1证明了其唯一解的性质。

与GRPO及Policy Gradient Methods比较

我们先比较GVPO与其余算法的结构相似性。为了简洁我们在这一节假设 $\beta =1$ 。我们将 ${\hat{\mathcal{L}}}_{\text{GVPO}}$ 展开并稍作变换可以得到其在梯度上等价于

$$-2{\mathbb{E}}_{x,y}[(R(x,y)-{\mathbb{E}}_{y}R(x,y))\log {\pi }_{\theta }(y|x)+Cov(\log {\pi }_{\theta },\log {\pi }_{{\theta }^{\prime }})-0.5Var(\log {\pi }_{\theta })]$$

其中

$$Var(\log {\pi }_{\theta })=(\log {\pi }_{\theta }(y|x)-{\mathbb{E}}_y\log {\pi }_{\theta }(y|x){)}^2，Cov(\log {\pi }_{\theta },\log {\pi }_{{\theta }^{\prime }})=(\log {\pi }_{\theta }(y|x)-{\mathbb{E}}_y\log {\pi }_{\theta }(y|x))(\log {\pi }_{{\theta }^{\prime }}(y|x)-{\mathbb{E}}_y\log {\pi }_{{\theta }^{\prime }}(y|x))$$

可以发现GVPO的loss里一共有三项：

• $(R(x,y)-{\mathbb{E}}_{y}R(x,y))\log {\pi }_{\theta }(y|x)$ 鼓励了最大化advantage。这在GRPO里的对应是标准化分数后的rewards。
• $Cov(\log {\pi }_{\theta },\log {\pi }_{{\theta }^{\prime }})$ 限制了 ${\pi }_{\theta }$ 不能过分偏离 ${\pi }_{{\theta }_{old}}$ ，对应于 ${\mathbb{D}}_{KL}[{\pi }_{\theta }(y|x)||{\pi }_{{\theta }^{\prime }}(y|x)]$ 。此外，在GVPO算法实现里设置了 ${\pi }_{{\theta }^{\prime }}={\pi }_{{\theta }_{old}}$ ，实际上对应了PPO和TRPO的trust-region限制，这保证了policy在更新过程中的稳定性。
• $Var(\log {\pi }_{\theta })$ 平衡了探索exploration与利用exploitation。这一项对应于熵正则 $-{\mathbb{E}}_y\log \pi (y|x)$ 。增加熵鼓励更多的探索性，分布会趋于均匀分布。但可能会限制高质量response的概率。反之，减少熵加速了收敛，但会在多样性上带来问题。因此，实践中如何决定熵正则的系数十分困难和敏感。而 $Var(\log {\pi }_{\theta })$ 先天的支持将低质量的response概率为0而高质量的response概率尽可能接近。即概率分布可以呈现蛋糕状(cake is not a lie!)。

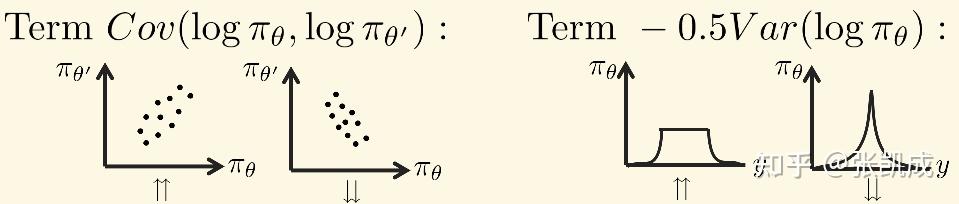
我们进一步比较GVPO和Policy Gradient Methods更深层次的区别。实践中，Policy Gradient Methods为了保证更新的稳定性，会在最大化reward的过程中使用KL散度的惩罚限制 ${\pi }_{\theta }$ 偏离 ${\pi }_{{\theta }_{old}}$ 的程度，即：

$${\nabla }_{\theta }[{\mathbb{E}}_{x,y\sim {\pi }_{\theta }(y|x)}[R(x,y)]-{\mathbb{D}}_{\text{KL}}[{\pi }_{\theta }||{\pi }_{{\theta }_{\text{old}}}]]$$
$$={\mathbb{E}}_{x,y\sim {\pi }_{\theta }(y|x)}(R(x,y)-\log \frac{{\pi }_{\theta }(y|x)}{{\pi }_{{\theta }_{\text{old}}}(y|x)}){\nabla }_{\theta }\log {\pi }_{\theta }(y|x)$$

这带来一个问题，即必须从当前的policy ${\pi }_{\theta }$ 中采样，带来低采样效率的问题。作为一种解决方式，可以引入重要性采样：

$$={\mathbb{E}}_{x,y\sim {\pi }_{{\theta }_{\text{old}}}(y|x)}\frac{{\pi }_{\theta }(y|x)}{{\pi }_{{\theta }_{\text{old}}}(y|x)}\left(R(x,y)-\log \frac{{\pi }_{\theta }(y|x)}{{\pi }_{{\theta }_{\text{old}}}(y|x)}\right){\nabla }_{\theta }\log {\pi }_{\theta }(y|x)$$

重要性采用使得可以从之前的policy ${\pi }_{{\theta }_{old}}$ 中采样。然而其中带来了重要性采样系数 $\frac{{\pi }_{\theta }(y|x)}{{\pi }_{{\theta }_{\text{old}}}(y|x)}$ ，当 ${\pi }_{\theta }$ 和 ${\pi }_{{\theta }_{old}}$ 差别较大时会带来梯度爆炸或者梯度消失等问题。PPO和GRPO等算法在实践中采用了clip技术，强制限制重要性采样系数不要过大或过小。但因此，clip会导致无偏性消失并带来各种各样的问题。

作为对比，GVPO就没有这些问题，因为GVPO从一开始就不需要on- policy采样。将上述Policy Gradient Methods内减去一个常数可以得到：

$${\mathbb{E}}_{x,y\sim {\pi }_{\theta }(y|x)}\left[R(x,y)-\log \frac{{\pi }_{\theta }(y|x)}{{\pi }_{{\theta }_{\text{old}}}(y|x)}-{\mathbb{E}}_{y\sim {\pi }_{\theta }(y|x)}\left(R(x,y)-\log \frac{{\pi }_{\theta }(y|x)}{{\pi }_{{\theta }_{\text{old}}}(y|x)}\right)\right]{\nabla }_{\theta }\log {\pi }_{\theta }(y|x)$$

作为对比，GVPO的梯度是：

$${\mathbb{E}}_{x,y\sim {\pi }_s(y|x)}\left[R(x,y)-\log \frac{{\pi }_{\theta }(y|x)}{{\pi }_{{\theta }_{\text{old}}}(y|x)}-{\mathbb{E}}_{y\sim {\pi }_s(y|x)}\left(R(x,y)-\log \frac{{\pi }_{\theta }(y|x)}{{\pi }_{{\theta }_{\text{old}}}(y|x)}\right)\right]{\nabla }_{\theta }\log {\pi }_{\theta }(y|x)$$

由此可见带KL约束的Policy Gradient Methods其实是GVPO当 ${\pi }_s={\pi }_{\theta }$ 的一种特例！这也体现出GVPO能将采样分布 ${\pi }_s$ 解耦带来的优势：一方面避免了on-policy样本利用率低的缺点，另一方面也避免了现有off-policy方法的重要性采样带来的缺点。

总结

本文的封面概括了GVPO的核心内容：

• 蓝色部分。我们从梯度权重 w 出发设计了GVPO loss，通过与policy gradient对比，体现了GVPO具有采样丰富性的优势。
• 红色部分。GVPO可以表示成真实reward和隐式reward的MSE形式。从MSE形式可以进一步推导出GVPO理论唯一最优解的优良性质。
• 黄色部分。通过拆解GVPO loss，可以从正则项的角度说明GVPO的稳定性。

此外，GVPO的实现十分简单，文章中展示了在verl框架下如何只修改几行代码实现GVPO。

论文：GVPO: Group Variance Policy Optimization for Large Language Model Post-Training
链接：https://arxiv.org/abs/2504.19599

感谢熊辉教授，洪定乾老师和各位合作者对本工作的支持。

欢迎讨论:-)