陶哲轩疯狂安利Copilot：它帮我完成了一页纸证明，甚至能猜出我后面的过程

克雷西 发自 凹非寺
量子位 | 公众号 QbitAI

继给GPT-4“代言”之后，Copilot也被陶哲轩疯狂安利。

他直言，在编程时，Copilot能直接预测出他下一步要做什么。

有了Copilot之后，研究做起来也更方便了，陶哲轩也用它辅助自己完成了最新的研究成果。

陶哲轩说，这次的论文中，有关这一部分的内容其实只有一页。

但具体完成这一页纸的证明，他足足写了200多行代码，用的还是新学的编程语言Lean4。

而在陶哲轩公开代码的GitHub页面上显示，Copilot将写代码的速度提升了一半以上。

陶哲轩介绍，之所以选择Lean4是看中了它的“重写策略”，也就是对一长段表达式进行针对性的局部替换。

举个例子，假如定义了一个复杂的函数f(x)，当我们想输入f(114514)的表达式时，直接用代码把x“重写”成114514就可以了。

陶哲轩说，这个特性相比于需要反复输入公式的LaTeX简直不要太方便。

那么陶哲轩这次的“一页纸证明”又给我们带来了什么新成果呢？

一页纸证明新不等式

这篇论文谈论了有关麦克劳林不等式的问题。

麦克劳林不等式是数学中一个经典的不等式，它基于“非负实数的算数平均值大于等于几何平均值”这一定律导出，可以表述为：

设y₁…y_n为非负实数，对k=1…n，定义均值S_k为（分母为分子的项数）：

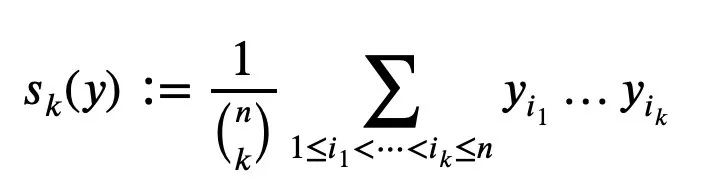
它作为具有根的 n 次多项式的归一化系数而出现。

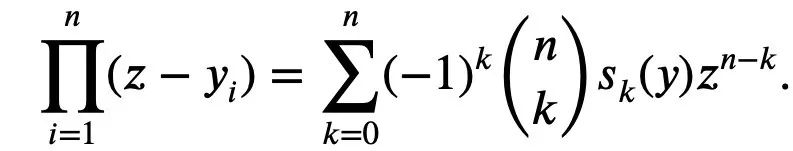
（记住这个式子，我们称它为式1）

则麦克劳林不等式可以表示为：

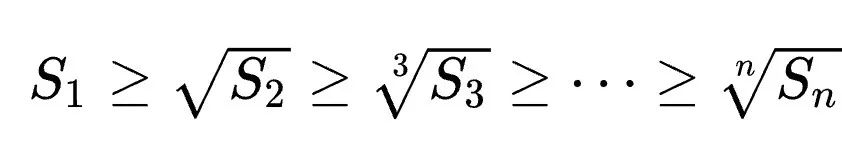
其中，当且仅当所有y_i相等时等号成立。

在微积分中，还有一个经典的牛顿不等式：

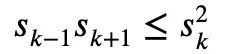
对任意1≤k<n，如果实变量y1…y_n均为非负，牛顿不等式就可以简单地描述麦克劳林不等式了：

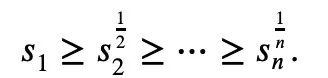
但如果不加上这个限制条件，即允许负数项的存在，用牛顿不等式就无法表示麦克劳林不等式了。

于是针对牛顿不等式中可能存在负数项的情况，陶哲轩提出了一组新的不等式变体：

对任意r>0且1≤ℓ≤n，必有式2或式3成立。

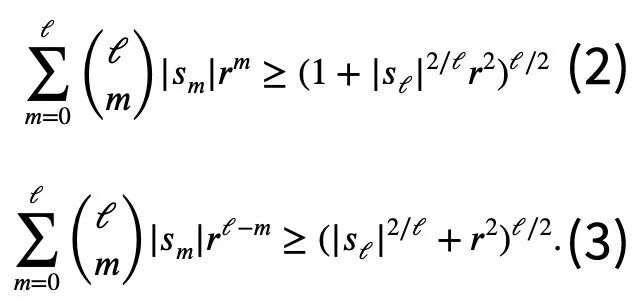
这便是陶哲轩这一页纸所要证明的内容，具体证明过程是这样的：

不妨构建一个关于复杂变量z的多项式P(z)：

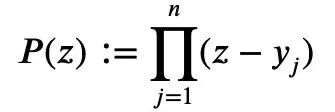
由前面的式1和三角不等式可得：

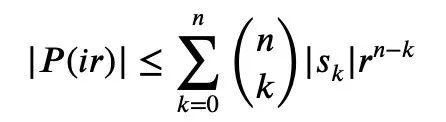
所以只需要建立下界：

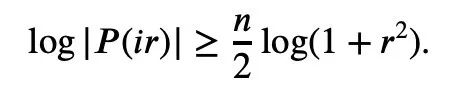
对P(z)取绝对值再取对数可得：

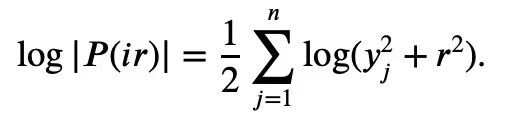
由于对任意实数t，t ↦ log(e^t+a)呈凸性且a>0，可以得到不等式：

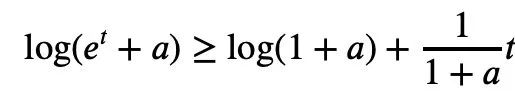
当a=r²，t=2log y_j时，可以得出：

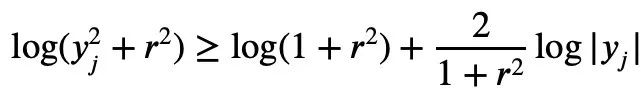
以上就是陶哲轩给出的证明过程，但是，当归一化的|S_n|=1时，下式成立：

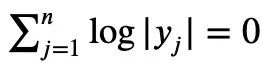
下一步：建立细化版本

除了这次提到的“一页纸证明”，陶哲轩的这篇论文中还提出了另一项新的定理，即对任意 1 ≤ k ≤ ℓ≤ n.：

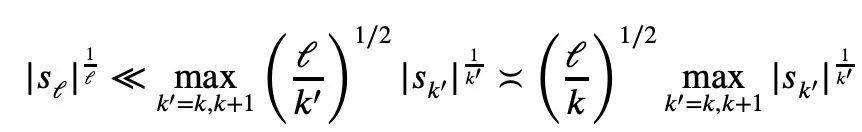
在博客文章中，陶哲轩透露，他的下一步计划就是提出这一不等式的细化版本。

陶哲轩说，证明的过程“就像练习一样”会很简单，用微积分就能搞定。

不过，他也提到会有一个小困难，因为这部分论证过程使用到了渐进符号。

新的结论具体怎样，让我们拭目以待。

One More Thing

陶哲轩可谓是AI工具的忠实粉丝，Copilot、GPT-4，还有一些其他辅助工具都受到过他的推荐。

这次，他还对大模型的发展提出了新的期待，希望有一天模型可以直接生成不等式变体。

论文地址：
https://arxiv.org/abs/2310.05328 

参考链接：
https://mathstodon.xyz/@tao/111271244206606941

— 完 —

「量子位2023人工智能年度评选」开始啦！

今年，量子位2023人工智能年度评选从企业、人物、产品/解决方案三大维度设立了5类奖项！欢迎扫码报名 

MEET 2024大会已启动！点此了解详情。

点这里👇关注我，记得标星哦～