Datawhale 春训营 材料设计赛道 篇二

概述

随着深度学习技术的发展和定量构效关系(Quantitative structure–activity relationship, QSAR)数据的剧增, 多种深度生成模型联合强化学习或贝叶斯优化算法在生成具有理想属性、新颖且多样的分子上显示出较大潜力, 这为学术界和制药行业大幅缩减了新药研发的时间和成本. 近年来基于深度学习的分子生成方法主要包括基于SMILES和基于分子图表示的方法. 尽管这些分子表示方法在各种应用中都很有效, 但更本质和更富含信息的分子表示是3D几何, 其中原子由其笛卡尔坐标表示. 在化学信息学和计算化学等领域处理3D分子构象至关重要, 这是因为它决定了分子的生物、化学和物理性质, 如电荷分布、势能、分子对接、药效团搜索等. 比如在药物设计中, 理解分子如何与特定的靶蛋白结合至关重要, 而这一过程很大程度上取决于这两者的3D构象, 包括几何(形状匹配)和化学(疏水、亲水)相互作用[2]. 预测3D分子构象的传统方法包括实验测定和基于力场或量子力学的第一性原理预测, 这些方法十分耗时且成本高昂. 随着几何深度学习在处理几何图形数据上的快速发展[3], 近年来面向3D分子构象的深度生成模型逐渐成为研究热点.

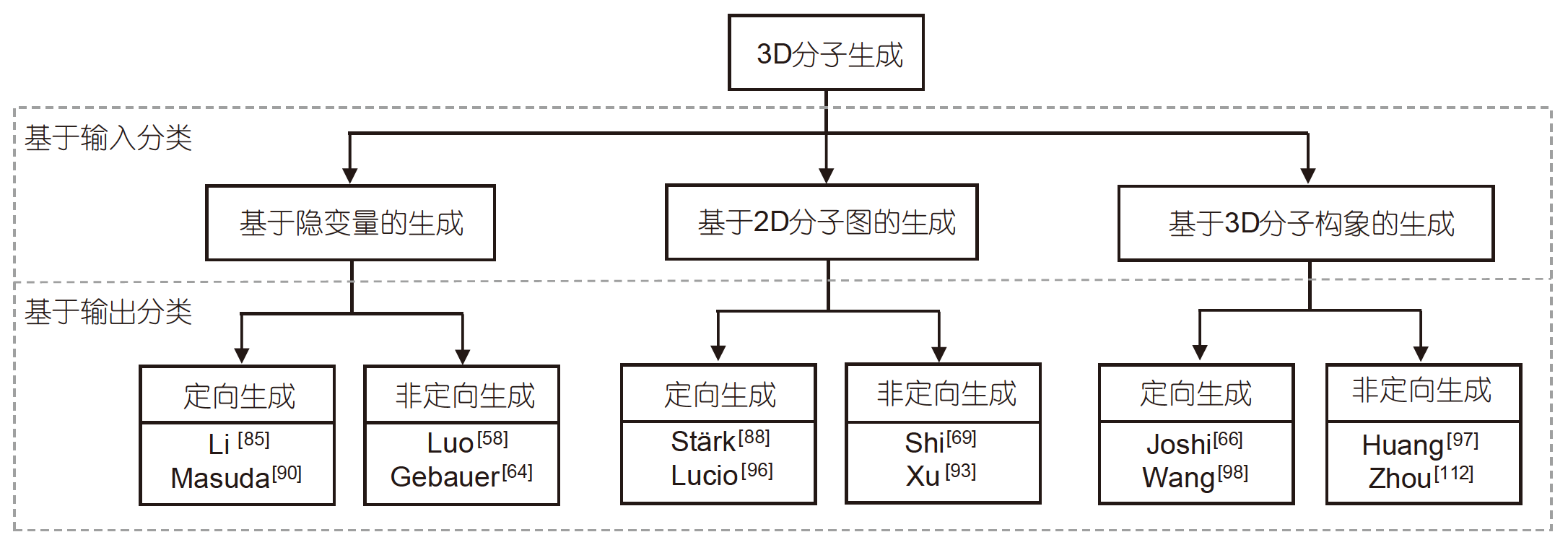
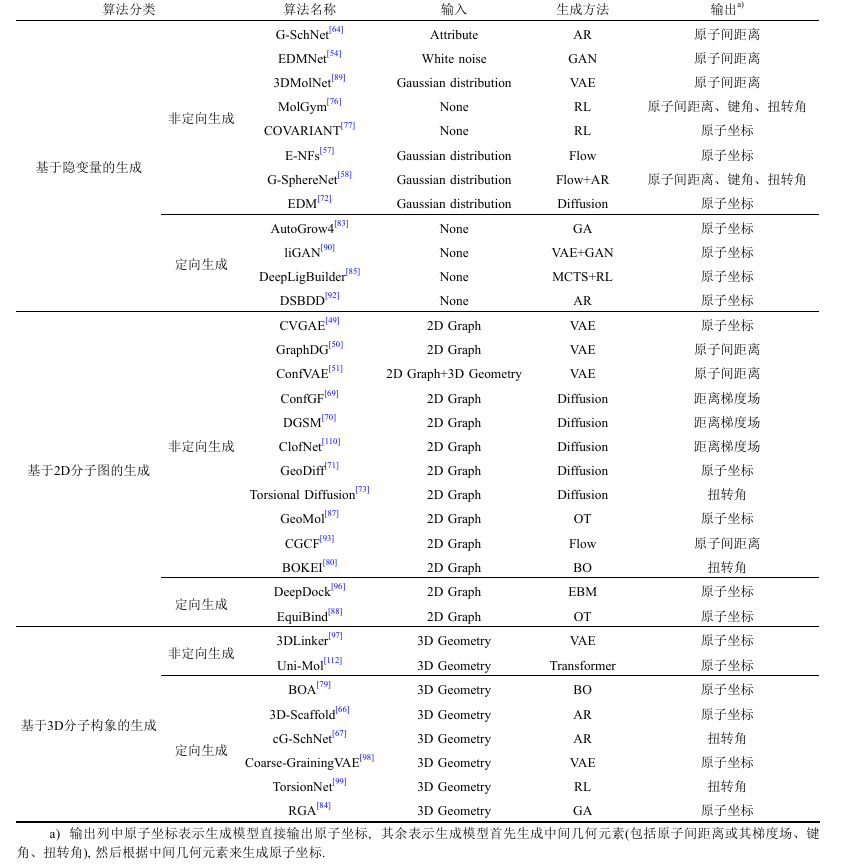
分子生成(molecular generation)利用深度学习技术来学习分子数据集的概率分布, 并生成具有理想生物活性和药代动力学属性的新颖分子. 分子生成通过在类药化学空间中搜索和采样多目标属性约束的新分子, 有效减小了搜索空间, 进而加速上述药物发现的进程. 现有的绝大多数基于字符串或基于图的分子生成方法由于缺乏空间信息而无法识别出空间异构体、原子间非键相互作用、以及分子和靶标蛋白在三维空间中的相互作用, 因而在实际药物设计场景中受到限制. 3D分子生成(3D molecular generation)有助于解决上述挑战, 旨在设计出具有理想生物化学属性和几何属性的新颖分子. 比如在基于受体结构的药物设计中, 不同于2D分子图的简化结构表示, 3D分子生成算法生成的3D构象可以在生成过程中考虑分子内或分子间相互作用, 以及来自蛋白口袋的局部约束, 因而能更好地保证预测的结构具有生物活性或药物属性. 根据生成算法的输入将现有的3D分子生成方法总结为三大类, 第1类基于隐变量的生成是指在没有给出参考分子的情况下生成3D分子构象, 即从零开始生成3D分子构象; 第2类基于2D分子图的生成是指给定2D分子图来生成或优化3D分子构象; 第3类基于3D分子构象的生成是指给定3D分子构象来生成或优化3D分子构象. 根据生成算法的输出将3D分子生成方法划分为定向生成和非定向生成. 非定向生成是指利用生成模型学习训练数据集的分布并从中采样出具有新颖、多样、化学有效以及几何有效(稳定态)等通用属性的3D分子构象. 定向生成是指在符合这些通用属性的基础上还需满足多种特定的生物活性和药物属性, 如对特定靶蛋白具有高结合亲和力、靶标选择性、化学可合成性、安全性等. 具体分类以及代表模型如图1和表1所示, 各方法的创新点和优劣性将在第3~5节着重讨论. 

 

3D分子生成是药物发现领域一个极具挑战的任务, 其存在的问题和难点主要包括以下几个方面: (1)搜索空间巨大: 由键长、键角和扭转角组成的三维结构空间巨大, 虽然分子图对可能的三维构象施加了特定的约束(例如键长范围取决于键类型, 四面体中心决定了局部原子的空间排列), 然而可能的构象空间随着图尺寸和可旋转键数量的增加呈指数增长, 这阻碍了穷尽探索的可能性. (2)对称性归纳偏置: 3D分子生成需要处理几何图形式的数据. 不同于一般的图数据, 几何图不仅为每个节点分配一个特征, 还为每个节点分配一个几何向量. 分子可以用几何图来表示, 其中原子的3D坐标是几何向量. 分子的3D构象在空间中具有旋转、平移的几何对称性, 这是因为分子在3D空间中发生旋转、平移后其3D坐标会发生变化, 但控制原子动力学的物理定律是不变的. 在处理分子的3D几何图数据时, 将对称性这种归纳偏置纳入模型设计是至关重要的, 这也推动了几何等变图神经网络的发展. (3)构象分布多模态: 一个分子体系的总能量随其结构的变化而改变的方式可以通过势能面来描述, 势能面上存在多个能量高点和低点, 其中最低处称为全局能量最低点, 其他能量较高的极小点则称为局部能量最低点. 真实的分子倾向于以能量较低的稳定态构象存在, 对应于势能面上的能量低点, 这个数量在一到几千之间变化, 如何有效搜索这些势能面上的局部能量最低点是一大挑战. 最近, 扩散模型凭借其强大的生成能力在建模复杂多模态构象分布上显示出优势, 能更好地生成高质量和多样性的结构. 我们将在下文介绍扩散模型在3D分子生成建模上的出色表现. 现有的机器学习模型正试图从不同角度解决上述挑战, 目前已有一些综述对此领域进行了报道[4~7]. 为了促进更多研究者的参与, 我们对3D分子生成模型从算法到应用的最新进展进行系统回顾. 本文主要内容安排如下: 首先, 概述了3D分子生成的基本概念; 其次, 梳理了基于隐变量的生成、基于2D分子图的生成和基于3D分子构象的生成这三种方法的研究进展, 每一种方法又根据3D分子生成算法的输出分为定向生成和非定向生成进行讨论; 随后, 总结了相关生成模型在主要的公开数据集上的性能, 来说明各种生成模型的优缺点; 最后, 对3D分子生成领域进行总结和展望. 

2 分子生成的基本概念

2.1 分子表示

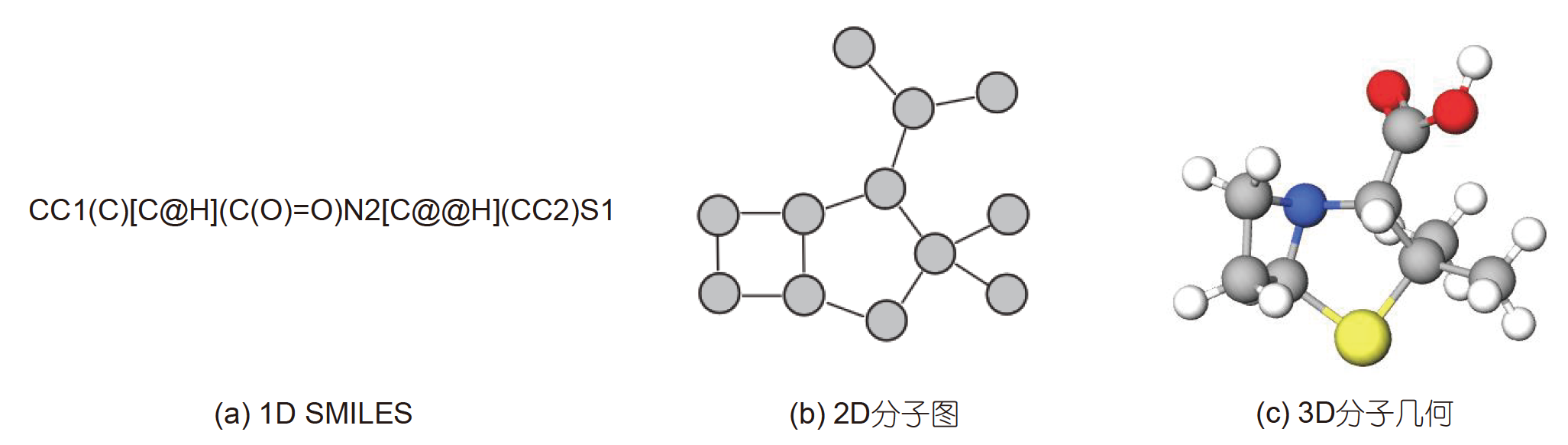
神经网络能将复杂的输入表示转换成解决特定任务所需的潜在空间的表示, 因此输入表示的选择对于模型如何学习分子信息至关重要. 在本节中, 我们将介绍分子表示(molecular representation)的三类主流方法: 1D字符串, 2D分子图和3D分子几何. 图2给出了一个特定分子(青霉烷)的三种表示方法示例.

 

2.1.1 1D字符串表示

最常见的1D字符串表示类型为简化分子线性输入规范(Simplified Molecular Input Line Entry System, SMILES), 由David Weininger和Arthur Weininger于1986年开发, 并由日光化学信息系统(Daylight Chemical Information Systems)改进和扩展[8]. SMILES是一种简单的基于ASCII字符的表示, 根据预定义的原子排序规则将一个分子转换成一个字符序列, 能够明确地描述原子、键、环、芳香性和立体化学等信息. 同一个分子由于起点原子差异可以表示成多个不同的SMILES, 实际使用时选择统一的规范化SMILES (Canonical SMILES)表示法, 而通用SMILES可用于数据增强. 由于SMILES基于序列表示的特性, 自然语言处理算法可以自然地被移植到分子生成领域. 先前的研究工作[9~12]利用循环神经网络(Recurrent Neural Network, RNN)、长短期记忆网络(Long Short-Term Memory, LSTM)等自回归生成模型生成分子的SMILES字符串. 这些方法忽略了SMILES语法的复杂性, 容易生成无效的SMILES, 即生成的SMILES不符合化合价规则导致不能转换成分子结构. 为了解决这个问题, Krenn等人[13]设计了一种改进的字符串表示方法, 称为自引用嵌入式字符串(Self-Referencing Embedded Strings, SELFIES), 基于SELFIES的RNN模型可以生成100%有效的分子. 另外, 在化学反应预测任务中, 上述针对单一分子设计的方法忽略了反应物和生成物SMILES之间的关系, 我们课题组[14]提出了一种用于化学反应预测的紧凑的分子字符串表示R-SMILES, 通过将输入和输出SMILES的根原子进行对齐的方式, 避免模型学习复杂的SMILES语法, 从而专注于学习化学反应相关的化学知识. 此外, 1D字符串表示还包括国际化学物标识(International Chemical Identifier, InChI)[15]和SMARTS(SMiles ARbitrary Target Specification)[16].

import pickle

# 替换为你的 .pkl 文件路径
pkl_file_path =path to competition/data/competition/competition_smiles.pickle'

# 加载 .pkl 文件
with open(pkl_file_path, 'rb') as file:
    data = pickle.load(file)

# 显示内容
data

['O=C1NCCC1c1ccc(Cl)cc1',
 'C1C2CC12',
 'O=S1(=O)CCN(S(=O)(=O)CC2CCCCC2)CC1',
 'O=C(Cc1cnco1)N1CCNCC1',
 'c1csc(C(c2nnn[nH]2)N2CCCCC2)c1',
 'CC(=O)OC1CNC1=O',
 'O=C(O)CC1NC=NC1=O',
 'O=c1[nH]c(=O)n2ccnc2[nH]1',
 'Cc1cccc(=O)o1',
 'CCOC1C=NOC1',
 'O=C1CCCC/C=C/CCO1',
 'O=C1NCCN1CCc1ccccc1',
 'N=C(Nc1ccc(Cl)cn1)Nc1nccs1',
 'CN(C)/N=C/c1c[nH]c(=O)[nH]c1=O',
 'O=Cc1cc(F)c(F)c(F)c1',
 'CC(O)OC(N)=O',
 'CCN/C(O)=C1/N=CC=CC1=O',
 'NC(=O)Oc1c(F)c(F)c(F)c(F)c1F',
 'NC(=O)N1CCOCC1',
 'CN(C1CCNCC1)S(=O)(=O)c1cccc(Cl)c1',
 'O=c1ocnc2ccc(Cl)cc12',
 'O=[SH](=O)N1CCCNC1',
 'C1=C(N2CCOCC2)CCCC1',
 'COC(=O)NC1=NNC(=O)C1',
 'O=C1N=CSC1F',
...
 'O=C(Cn1cnnn1)N1CCOCC1',
 'O=S(=O)(NCc1ccccc1F)c1ccc(F)cc1F',
 'O=C(c1ccc(Cl)nc1)N(C(O)=S)c1ccc(Cl)cc1',
 'NS(=O)(=O)CC1CCCCC1',
 ...]
Output is truncated. View as a scrollable element or open in a text editor. Adjust cell output settings...

2.1.2 2D分子图表示

表示分子更直观的方法是根据分子的路易斯结构将其转化成一个分子图(molecular graph), 其中原子表示成节点, 化学键表示成边, 并根据原子类型和化学键类型为节点和边赋值对应的标签. 与1D字符串表示相比, 2D分子图表示具有如下优势: 一方面, 图表示能直接捕获原子之间的连接, 而该信息在1D字符串表示中需要模型学习其复杂的语法规则; 另一方面, 如上文所述, 基于SMILES的分子生成方法无法确保生成的分子具有100%化学有效性, 而基于2D分子图的生成方法很容易确保生成的分子是100%化学有效的. 近年来已有许多研究工作致力于开发能生成真实分子图的神经网络架构. 2D分子生成根据生成策略可分为三类: (1)一次输出图的节点类型和邻接矩阵来生成分子图, 有许多深度生成模型可以一次性生成整个分子, 如基于变分自编码器(Variational Autoencoder, VAE)的VGAE[17]、RVAE[18]、GraphVAE[19], 基于生成对抗网络(Generative Adversarial Network, GAN)的MolGAN[20], 基于流(Flow)模型的GraphNVP[21]等. (2)基于子结构生成分子图, 即将子结构或官能团作为构建块来生成高质量的分子. 代表性模型有基于VAE的JT-VAE[22]、HierVAE[23], 基于强化学习(Reinforcement Learning, RL)的RationaleRL[24]、MolEvol[25], 基于采样的MARS[26]、MIMOSA[27]等. (3)通过顺序添加节点和边生成分子图, 代表性模型有基于VAE的CGVAE[28], 基于RL的GCPN[29]、DeepGraphMolGen[30], 基于Flow的GraphAF[31]、GraphDF[32]等.

2.1.3 3D分子几何表示

现有的基于1D字符串或2D分子图的生成模型没有考虑化合物分子的空间构象, 例如同分异构体具有一样的拓扑结构, 但其3D空间结构是不同的. 捕获3D空间结构特征对于准确预测分子的物理化学性质如量子性质、分子构象生成至关重要. 因此, 更本质和更有信息的分子表示是3D几何(3D geometry), 又称3D分子构象(3D molecular conformation), 它包含了3D几何信息(如位置)和重要的物理规律(如对称性). 3D几何将原子坐标加入到它们的表示中, 并能够描述三维空间中原子之间的相对位置. 这里我们考虑处于平衡态的构象, 对应于势能面上的局部最低点. 与1D字符串和2D分子图表示相比, 3D几何表示显著扩展了有待探索的分子空间, 同时也增加了难度, 主要挑战在于模型需要在3D空间中对旋转和平移操作保持等变性. 最近, 3D分子几何表示的研究工作在探索等变性上主要通过以下两种策略, 一种是等变图神经网络, 代表性工作有SE(3)-Transformers[33], EGNN[34]等; 另一种是借助中间几何元素如原子间距离和角度信息来使用E(3)不变的三维信息, 代表性工作有SchNet[2], PhysNet[35], DimNet[36]等. 下文将详细介绍该领域现有的研究进展并对其进行分类整理. 此外, 分子的3D表示还包括3D密度图(3D density map)和3D表面网格(3D surface mesh). 分子的3D密度图由组成分子的所有原子的体积组成[37], 常用3D网格(3D grid)表示, 可用3D卷积神经网络(3D Convolutional Neural Network, 3DCNN)对其进行编码[38]. 3D表面网格由定义分子表面形状的节点、边和面组成, 也常用3D网格表示, 可用测地线卷积神经网络(Geodesic Convolutional Neural Network, GCNN)[39]或3D图神经网络(3D Graph Neural Network, 3DGNN)[2]对其进行编码. 这些分子表示方法在分子生成任务中应用较少, 在这里仅作简单介绍以便读者了解.

2.2 等变图神经网络

2.2.1 等变性

物体(或系统)的对称性(symmetry)是指对其变换操作后, 物体的某一特性保持等变(equivariant)或不变(invariant)的性质[40]. 对称性在物理系统中无处不在, 例如动量守恒中的空间平移不变性, 分子构象、蛋白质或点云的旋转对称性. 在建模物理系统时, 赋予深度学习模型这种归纳偏置对于模型的训练和泛化能力都至关重要. 下面给出等变性的定义和相关符号说明.

E(n)等变(E(n)-equivariance)是指模型在n维欧式空间中对平移、旋转、反射具有等变性[41]. 设有一个函数ϕ:X→Yϕ:X→Y, XX是输入, YY是输出, 定义某变换群GG, 对于任意群元素g∈Gg∈G, 若有

ϕ(Tg(x))=Sg(ϕ(x))(1)

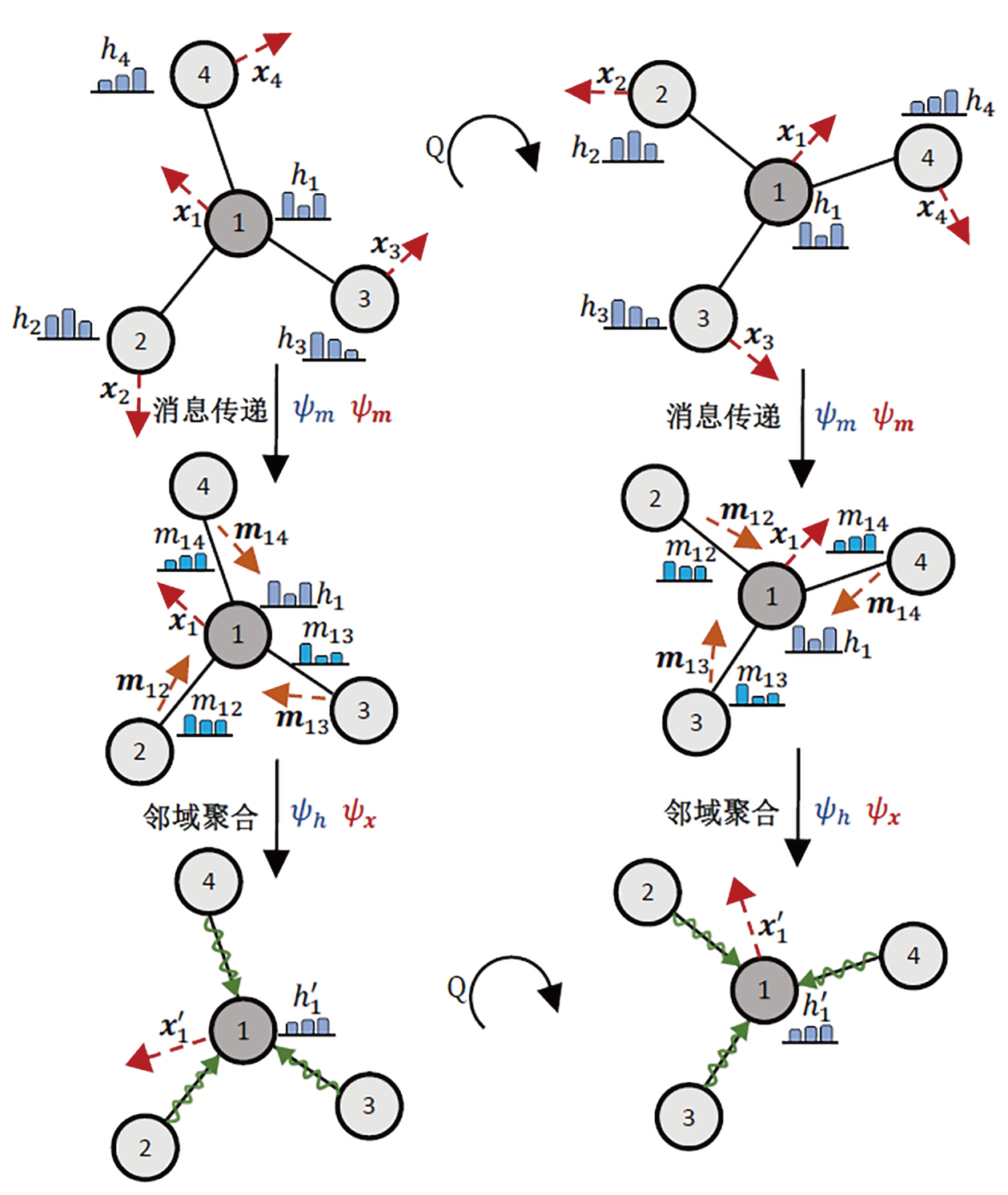
则称函数ϕϕ对变换群GG是等变的, 其中TgTg指变换gg在输入空间中的群表示, SgSg是指同一个变换gg在输出空间中的群表示, 上式说明了对输入的变换操作等同于对输出施加相同的变换. 当Sg=ISg=I, 即输出的群表示是单位矩阵时, 式(1)表示不变性(invariance), 即对输入做群中的任何变换, 输出保持不变. 神经网络ϕ:y=ϕ(x)ϕ:y=ϕ(x)的E(n)E(n)等变性包括以下三种对称性变换, 图3展示了其中的旋转等变性.

(1)平移等变性(translation equivariance): 对输入施加一段平移g∈Rng∈ℝn, 则输出也发生了同样的平移, 有y+g=ϕ(x+g)y+g=ϕ(x+g).

(2)旋转等变性(rotation equivariance): 对输入进行旋转导致输出也发生同样的旋转, 用正交矩阵Q∈Rn×nQ∈ℝn×n表示旋转变换, 则有Qy=ϕ(Qx)Qy=ϕ(Qx).

(3)反射等变性(reflection equivariance): 对输入关于平面(或直线)作反射(翻转)后得到输出, 即输入和输出互为镜像, 用正交矩阵P∈Rn×nP∈ℝn×n表示反射变换, 则有Py=ϕ(Px)Py=ϕ(Px).

2.2.2 图神经网络

图神经网络(Graph Neural Network, GNN)是近年来出现的一种利用神经网络来学习图结构数据, 提取发掘图结构数据中特征和模式的框架, 其优异的性能引起了学者的高度关注和深入探索[42]. 通过在图中的节点和边上制定一定的策略, GNN将图结构数据转化为规范而标准的表示, 并输入到多种不同的神经网络中进行训练, 在节点分类、边信息传播和图分类等任务上取得优良的效果. 当应用于分子时, GNN通过逐步聚合原子及分子环境的信息来提取特征. 下面给出 GNN 中相关符号的说明和定义.

图(Graph)是由节点(Vertex)和连接节点的边(Edge)构成, 记为G=(V,E)G=(V,E). 其中V={v1,v2,...,vn}V={v1,v2,...,vn}表示节点集合, E={e1,e2,...,em}E={e1,e2,...,em}表示边集合. 每个节点ii的节点特征表示为hihi, 连接节点i和j的边特征表示为eijeij. 近年来多种GNN框架被提出[43], 如图卷积神经网络(Graph Convolutional Network, GCN)、图注意力网络(Graph Attention Network, GAT)和图同构网络(Graph Isomorphism Network, GIN)等, 其中最流行的是Gilmer等人[44]提出的消息传递神经网络(Message Passing Neural Network, MPNN). MPNN将GNN统一到了一个通用的框架中, 它迭代地对每个节点或边进行消息传递和邻域聚合. MPNN的消息传播机制表示如下:

mij=ϕm(hi,hj,eij)hi=ϕh⎛⎜⎝∑j∈N(i)mij,hi⎞⎟⎠(2)mij=ϕm(hi,hj,eij)hi=ϕh(∑j∈N(i)mij,hi)(2)

其中mijmij是节点ii经消息传递后生成的信息, ϕmϕm和ϕhϕh分别是消息传递函数和邻域聚合函数, N(i)N(i)是节点i的邻居. 邻域聚合操作ϕhϕh满足置换等变性, 即改变输入顺序, 输出顺序也发生相应改变. 有几项研究工作利用该置换等变性在降低节点排列组合复杂度上的优势, 将GNN应用于具有几何输入的复杂系统, 例如粒子的三维坐标. 如Li等人[45]提出的动态粒子交互网络DPI-Net和Mrowca等人[46]提出的层次化关系网