蓝桥杯 左孩右兄弟【第十二届】【省赛】【A组】详解 C++ 动态规划/多叉树/二叉树/贪心

资源限制

时间限制：1.0s 内存限制：256.0MB

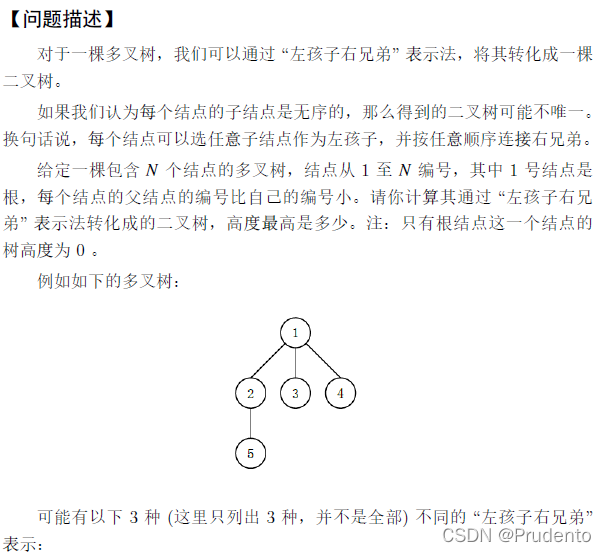
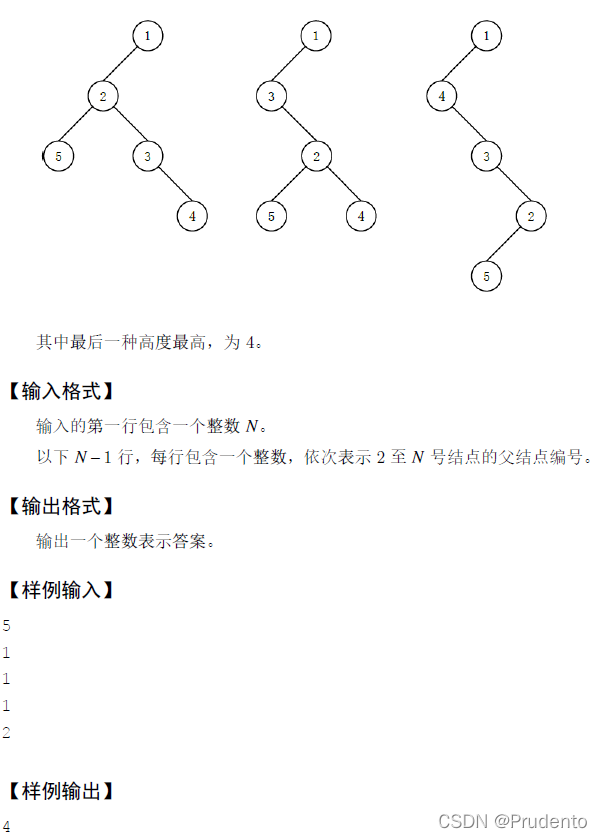
 思路简介

通过以下代码将多叉树转成二叉树

struct nod{
	int right,left;
}tree[MAXN];
//a是b的孩子
for(int i=1;i<=n;i++){
	scanf("%d %d",&a,&b);
	tree[a].right=tree[b].left;
	tree[b].left=a;
} 

将题目转化成求解二叉数的深度，会发现AC不了，因为此处的子结点连接是无序且不符合二叉树特点的。 因为此题中间结点们的连接方式并不重要，每个子树的最大深度只是取决于子结点的个数和所有子结点中的最大深度之和，所以此题感觉更像是高中所学的链式烃，求解烃的最大长度。

详解如下 

所以我们直接用vector实现邻接表存多叉树，不过这里需要存每一个孩子的结点编号。

戳以下链接粗略了解邻接表（不是本题重点）

C++ vector实现邻接表存图_Curz酥的博客-优快云博客_vector邻接表

 图的存储结构之邻接表(详解) - Angel_Kitty - 博客园

关键

要明白此处所谓的深度，此处子节点的连接方式是无序的，那么我们要想使得整个树的深度最大，那么每一个子树的深度都应该是最大的（有点贪心的思想）。那么如何使每一个子树的深度都是最大的？那就是对于每一个父结点，都遍历它的每一个子结点的深度，找到最大的子节点的深度，那么该父结点的最大深度=子节点个数+最大子节点深度——解释一下这句话：

因为此处的子节点的连接方式是无序的，所以当深度最大的子树放在最后，那么中间的子节点是如何连接的便无所谓了，并不会影响父结点的最大深度。

本题解采用dp，即动态规范的方法，dp[i]表示以i为根结点的子树的最大深度。而最终要求的便是dp[1]。所以应该采用自下而上更新的方式递推。利用vector <int>fa[100001]开一个二维数组 fa[i]便是以编号为i为父结点的子结点们。录入时相应子结点编号加入数组中。并对dp[i]进行初始化，

dp[i]=fa[i].size()。即在遍历每个父结点的所有子结点从而找出最大的深度之前，先将dp[i]初始化为各父结点的子结点数。接下来遍历n~1个结点便可。

另外题解代码中采用了快读，即在大量数据时候可以加快读入

了解快读戳以下链接

 快读(快速读入)_yzyyylx的博客-优快云博客_c语言快读

 快读的作用C++_weixin_49582982的博客-优快云博客_快读的作用

AC代码如下

#include<bits/stdc++.h>
using namespace std;
#define MAXN 100001
int n, maxh, t, t1;
int h;
vector <int>fa[100001];//开一个二维数组
int dp[MAXN];//dp[i]表示以i为根结点的树的深度
//dp[i]递推式，应该是遍历i的每一个儿子树，选取最深的
inline int read() {//利用getchar比scanf/cin快实现大量数据的快读 
	char ch = getchar(); int x = 0, f = 1;//f来标注符号
	while (ch < '0' || ch > '9') {//读取可能存在的非数字字符
		if (ch == '-') f = -1;
		ch = getchar();
	} while ('0' <= ch && ch <= '9') {
		x = x * 10 + ch - '0';
		ch = getchar();
	} return x * f;
}
int max1;
int main() {
	scanf("%d", &n);
	for (int i = 2; i <= n; i++) {
		t = read();
		fa[t].push_back(i);//各父结点的子结点加入数组中
	}
	for (int i = n; i >= 1; i--) 
		dp[i] += fa[i].size();//先加上所有的儿子数
	for (int i = n; i >= 1; i--) {
		max1 = 0;
		if (fa[i].size()) {//如果该结点不是叶子结点
			for (int j = 0; j<fa[i].size(); j++) {//遍历所有儿子
			max1 = max(max1, dp[fa[i][j]]);//找到最大深度的子树
			}
			dp[i] += max1;//更新值
		}
	}
	printf("%d", dp[1]);//完美输出

	return 0;
}

 评测结果截图

另外，显然递归对树结构非常友好，所以也可采用递归解法，思路与dp法大致相同。

#include<bits/stdc++.h>
using namespace std;
int N;int f;vector<int> v[100005];
int height(int node)//node即当前结点编号
{
	int m=0;//初始化，记录子树的最大深度
	for(int i=0;i<v[node].size();i++)//遍历所有子结点
		m=max(m,height(v[node][i]));//递归,找最大高度的子结点
	return m+v[node].size();//高度+深度
}
int main()
{
	cin>>N;
	for(int i=2;i<=N;i++)
	{
		cin>>f;
		v[f].push_back(i);
	}
	cout<<height(1);//从根结点开始递归
	return 0;
}

 评测结果截图