一般书上的应力转轴公式和应变转轴公式:


拿出来看:
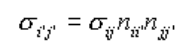
应变转轴公式类似
我个人感觉这个nii’和njj’有点不好理解,因为我很容易认为它们是相等的,进而我会认为公式是sigma*n*n
但是我又懒得自己动笔验证,于是用matlab算了一下
syms l1 l2 l3 m1 m2 m3 n1 n2 n3 sigmax sigmay sigmaz txy txz tyz real;
sigma=[sigmax txy txz;txy sigmay tyz;txz tyz sigmaz];
n=[l1 m1 n1;l2 m2 n2;l3 m3 n3];
sigma1=sigma*n*n; %我对书本的理解
sigma2=n*sigma*n'; %我猜测的正确形式
其中
sigma =
[sigmax, txy, txz]
[ txy, sigmay, tyz]
[ txz, tyz, sigmaz]
n =
[l1, m1, n1]
[l2, m2, n2]
[l3, m3, n3]
计算结果
sigma1 =
[l1*(l1*sigmax + l2*txy + l3*txz) + l2*(m1*sigmax + m2*txy + m3*txz) + l3*(n1*sigmax + n2*txy + n3*txz), m1*(l1*sigmax + l2*txy + l3*txz) + m2*(m1*sigmax + m2*txy + m3*txz) + m3*(n1*sigmax + n2*txy + n3*txz), n1*(l1*sigmax + l2*txy + l3*txz) + n2*(m1*sigmax + m2*txy + m3*txz) + n3*(n1*sigmax + n2*txy + n3*txz)]
[l1*(l2*sigmay + l1*txy + l3*tyz) + l2*(m2*sigmay + m1*txy + m3*tyz) + l3*(n2*sigmay + n1*txy + n3*tyz), m1*(l2*sigmay + l1*txy + l3*tyz) + m2*(m2*sigmay + m1*txy + m3*tyz) + m3*(n2*sigmay + n1*txy + n3*tyz), n1*(l2*sigmay + l1*txy + l3*tyz) + n2*(m2*sigmay + m1*txy + m3*tyz) + n3*(n2*sigmay + n1*txy + n3*tyz)]
[l1*(l3*sigmaz + l1*txz + l2*tyz) + l2*(m3*sigmaz + m1*txz + m2*tyz) + l3*(n3*sigmaz + n1*txz + n2*tyz), m1*(l3*sigmaz + l1*txz + l2*tyz) + m2*(m3*sigmaz + m1*txz + m2*tyz) + m3*(n3*sigmaz + n1*txz + n2*tyz), n1*(l3*sigmaz + l1*txz + l2*tyz) + n2*(m3*sigmaz + m1*txz + m2*tyz) + n3*(n3*sigmaz + n1*txz + n2*tyz)]
sigma2 =
[l1*(l1*sigmax + m1*txy + n1*txz) + m1*(m1*sigmay + l1*txy + n1*tyz) + n1*(l1*txz + n1*sigmaz + m1*tyz), l2*(l1*sigmax + m1*txy + n1*txz) + m2*(m1*sigmay + l1*txy + n1*tyz) + n2*(l1*txz + n1*sigmaz + m1*tyz), l3*(l1*sigmax + m1*txy + n1*txz) + m3*(m1*sigmay + l1*txy + n1*tyz) + n3*(l1*txz + n1*sigmaz + m1*tyz)]
[l1*(l2*sigmax + m2*txy + n2*txz) + m1*(m2*sigmay + l2*txy + n2*tyz) + n1*(l2*txz + n2*sigmaz + m2*tyz), l2*(l2*sigmax + m2*txy + n2*txz) + m2*(m2*sigmay + l2*txy + n2*tyz) + n2*(l2*txz + n2*sigmaz + m2*tyz), l3*(l2*sigmax + m2*txy + n2*txz) + m3*(m2*sigmay + l2*txy + n2*tyz) + n3*(l2*txz + n2*sigmaz + m2*tyz)]
[l1*(l3*sigmax + m3*txy + n3*txz) + m1*(m3*sigmay + l3*txy + n3*tyz) + n1*(l3*txz + n3*sigmaz + m3*tyz), l2*(l3*sigmax + m3*txy + n3*txz) + m2*(m3*sigmay + l3*txy + n3*tyz) + n2*(l3*txz + n3*sigmaz + m3*tyz), l3*(l3*sigmax + m3*txy + n3*txz) + m3*(m3*sigmay + l3*txy + n3*tyz) + n3*(l3*txz + n3*sigmaz + m3*tyz)]
单看第一项,
sigma1的l1*(l1*sigmax + m1*txy + n1*txz) + m1*(m1*sigmay + l1*txy + n1*tyz) + n1*(l1*txz + n1*sigmaz + m1*tyz)不正确,而sigma2的l1*(l1*sigmax + m1*txy + n1*txz) + m1*(m1*sigmay + l1*txy + n1*tyz) + n1*(l1*txz + n1*sigmaz + m1*tyz)正确,说明简洁的公式可以写成:sigma转=n*sigma原*n'
展开式为:

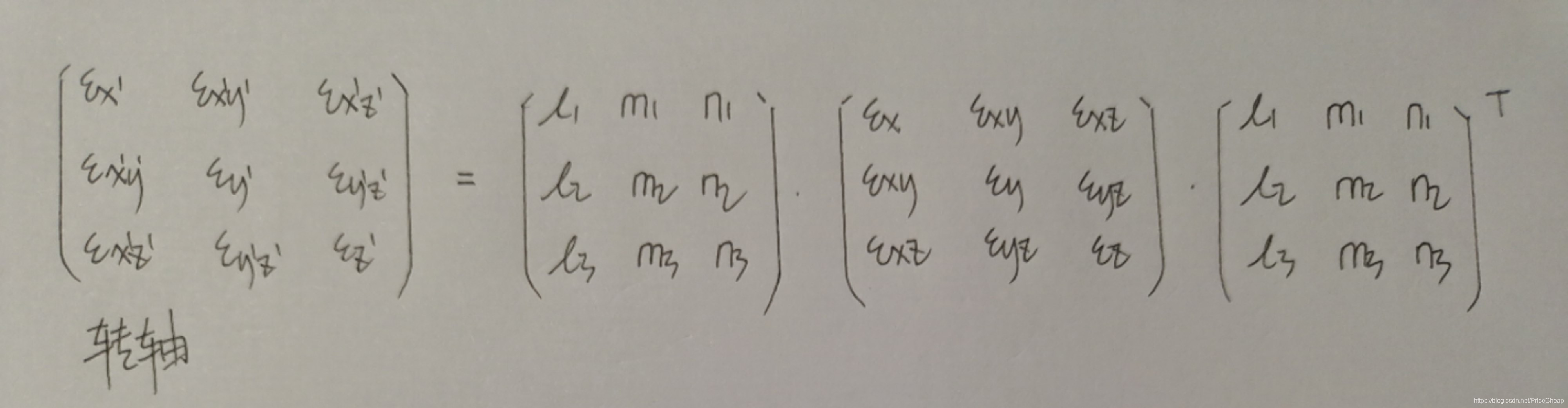




 本文探讨了应力转轴公式和应变转轴公式的理解问题,特别是nii'和njj'的关系。通过MATLAB计算发现,直观的简化公式并不正确,正确形式为展开式。这一过程强调了数学验证在理论理解中的重要性。
本文探讨了应力转轴公式和应变转轴公式的理解问题,特别是nii'和njj'的关系。通过MATLAB计算发现,直观的简化公式并不正确,正确形式为展开式。这一过程强调了数学验证在理论理解中的重要性。

















 2894
2894

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








