矩阵快速幂模板

又是这个东西，真的挺简单的，还是来看看吧！
这里以经典的不能再经典的斐波那契数列(Fibonacci sequence)作为模板吧。

模板题

题目描述

Fibonacci数列是这样的：
F[1]=1
F[2]=1
F[3]=2
F[4]=3
…
F[N]=F[N-1]+F[N-2]
现在给你两个整数N和M，请你求出Fibonacci数列的第N项F[N]，然后输出F[N]模M的值即可。

输入格式

输入两个整数N和M。

输出格式

输出一个整数，即F[N]模M的值。

样例数据

输入

5 1000

输出

5

备注

【数据规模】
1≤n≤2 000 000 000；1≤m≤1 000 000 000。

算法讲解

显然同普通的f[n]=f[n-1]+f[n-2]的递推算法(O(n))不行了，那怎么办？
换个思路想想，我们既然希望把时间复杂度压到O(logn)，那就不能一项一项地求了，于是就会想到一种算法——快速幂。
那如何产生这个“幂”呢？那就得用结合乘方实现的矩阵转移，因为是要用矩阵乘法递推，那就请大家思考一个问题，如何用f[n-1],f[n-2]分别表示出f[n],f[n-1]呢？
结合斐波那契数列的性质，不难得出答案：

f[n]=1*f[n-1]+1*f[n-2]
f[n-1]=1*f[n-1]+0*f[n-2]

在这儿解释一下，之所以要用f[n-1]=1f[n-1]+0f[n-2]这么弱智的式子表示f[n-1]，目的是保持每个矩阵的规模相等（即均为1*2），这样才能使用矩阵乘法。
所以我们这儿就很自然的得到了我们的转移矩阵

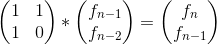
类似的，我们可以得到 ：
（f[n],f[n-1]）（上图中等式右边的矩阵）=({1,1},{1,0})（上图中最左边的矩阵）^n-2*（f[2],f[1])（1*2的矩阵）。
现在我们就可用快速幂以O(logn)的速度求出上式中0、1矩阵的n-2次方了。

看看代码吧！

Code

#include<bits/stdc++.h>
using namespace std;

struct node//要在函数间传址的矩阵建议用结构体，因为二维数组不好传址
{
	long long matrix[5][5];
}ans,bas;

int n,mod;

void matrix_fastpower(node &a,node &b,node &c)//矩阵乘法模板
{
	node t;
	for(int i=1;i<=2;i++)
	{
		for(int j=1;j<=2;j++) t.matrix[i][j]=0;
	}
	for(int i=1;i<=2;i++)
	{
		for(int j=1;j<=2;j++)
		{
			for(int k=1;k<=2;k++) t.matrix[i][j]=(t.matrix[i][j]+(a.matrix[i][k]%mod*b.matrix[k][j]%mod))%mod;
		}
	}
	c=t;
}

int main()
{
	scanf("%d %d",&n,&mod);
	ans.matrix[1][1]=1;//把ans矩阵构造成单位矩阵，相当于1
	ans.matrix[2][2]=1;
	bas.matrix[1][1]=1;
	bas.matrix[1][2]=1;
	bas.matrix[2][1]=1;
	int b=n-2;
	while(b)//快速幂模板
	{
		if(b&1) matrix_fastpower(ans,bas,ans);
		matrix_fastpower(bas,bas,bas);
		b=b>>1;
	}
	cout<<(ans.matrix[1][1]+ans.matrix[1][2])%mod;
	return 0;
}

学习厌倦了？点我有更多精彩哦！