分治策略之棋盘覆盖的C++实现

当k>0时，将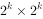的棋盘分割成四个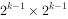子棋盘，特殊的方格必然位于4个较小的子棋盘之一，其余三个子棋盘中无特殊方格。为了将这个三个无特殊方格的子棋盘转化为特殊的棋盘，我们可以用一个L型骨牌覆盖这3个较小棋盘的汇合处，这3个棋盘上被L型骨牌覆盖的方格就成为该棋盘上的特殊方格，从而将原问题转化为4个规模较小的棋盘覆盖问题。递归的使用这种分割，直至棋盘简化为1*1棋盘。

#include <iostream>

#include <cstring>

#include <stdlib.h>

#include <algorithm>

using namespace std;

//全局整型变量，用来表示L型骨牌的编号

const int Board_size=4;

int tile=1;

int Board[4][4];