本文探讨了Dijkstra和SPFA两种算法在计算最短路径计数时的区别。Dijkstra算法中，每个点只会对其他点最多松弛1次，而SPFA则可能需要额外的策略来确保正确性。通过举例说明，指出在SPFA中，当节点2的最短路径多次加到节点4上时，需要在松弛操作后清零当前队首的最短路径计数，以确保每次对其他点的修改为1。同时，文章提到了特殊情况下的处理方式，并提供了两种版本的算法代码实现。
由于Dijkstra每个点被“操作”完了后就不会再进行对其他点的松弛操作，而SPFA会入队多次，这就造成了它们在最短路计数实现上的不同
先说Dijkstra的思路，给每个点记一个ans[i]表示源点到当前点最短路的条数
若需要松弛，那么直接ans[y]=ans[x]
否则
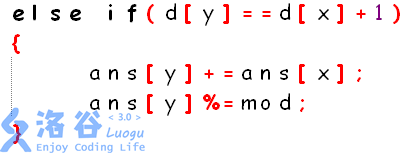
这个是非常好理解的，正确性也显然——每个点只会对其他点最多松弛1次。
而SPFA不能直接套用，一个显然的例子是
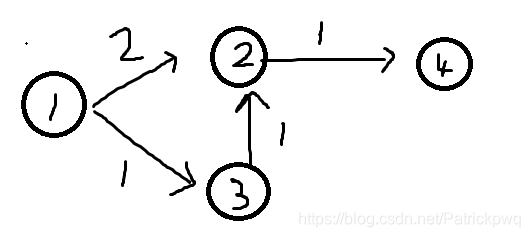
若直接套用会输出3。读者自行手玩一下就会发现，节点2的ans，多次加到了4身上。
那怎么改进呢？一种可行的方式是对于ans数组和now(当前队首)，在now进行松弛操作后清零now的ans。
若从当前点now走最短路到对应点vis有三种方式，清零的意义就在于使得每次对vis产生的修改都是1，而不是1,2,2或1,2,3。
另外还需注意在
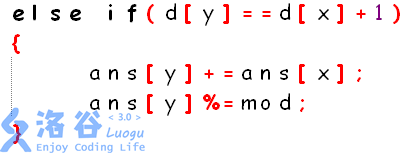
这种情况下y也要入队，否则又会少加。（数据5 5 1 2 1 2 3 1 3 4 1 4 5 1 1 4 3）
两种版本的代码：
#include<bits/stdc++.h>
const int N=2005;
con
最低0.47元/天 解锁文章
扫一扫
3412
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
