判断是否是二叉搜索树

二叉查找树 

二叉查找树(Binary Search Tree)，(又:二叉搜索树，二叉排序树)它或者是一棵空树，或者是具有下列性质的二叉树: 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树

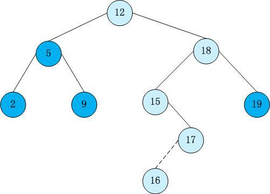
 解题思路：

利用中序遍历，如果是二叉搜索树，其中序遍历的结果一定是升序的，只需要将中序遍历稍加改变，在每个元素出栈时与前一个元素比较，看其是否大于前一个元素。

 

import java.util.Stack;
/**
 * Definition for binary tree
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
//利用中序遍历
public class Solution {
    public boolean isValidBST(TreeNode root) {
        //空树返回ture，空树是二叉搜索树
        if(root == null)
            return true;
        Stack<TreeNode> stack = new Stack<TreeNode>();
        //与前序遍历不同，一开始先不入栈
        TreeNode current = root;
        //记录出栈的node
        //作用是与下一个出栈的node进行数值比较，前一个要小于后一个才满足二叉搜索树的条件
        TreeNode pre = null;
        //或的条件是因为一开始root没有入栈，此时栈空但没有遍历结束
        while(!stack.isEmpty()|| current != null){
           if(current != null){
                stack.push(current);
                current = current.left;
            }
            else{
                current = stack.pop();
                if(pre != null && pre.val>=current.val)
                    return false;
                pre = current;
                current = current.right;
            }
        }
        return true;
    }
}