高精度乘法--模拟

原题链接：蓝桥杯算法提高VIP-高精度乘法

题目描述

在C/C++语言中，整型所能表示的范围一般为-2^31到2^31（大约21亿）,即使long  long型，一般也只能表示到-2^63到2^63。要想计算更加规模的数，就要用软件来扩展了，比如用数组或字符串来模拟更多规模的数及共运算。

现在输入两个整数，请输出它们的乘积。

输入格式

两行，每行一个正整数，每个整数不超过10000位 

数据规模和约定：
每个整数不超过10000位

输出格式

一行，两个整数的乘积。 

样例输入

99 
101 

样例输出

9999

解题思路:

由于相乘之后的位数较大，已经超过了可存放整数的范围，需要开辟数组来存放乘积结果的每一位数。由于待相乘的两个整数也较大，需要分别使用两个数组存放，然后将乘积结果存放在另一个更大的整型数组中，所以关键就是怎么使用两个数组来模拟乘法计算。

首先一起来回顾一下小学的乘法计算：

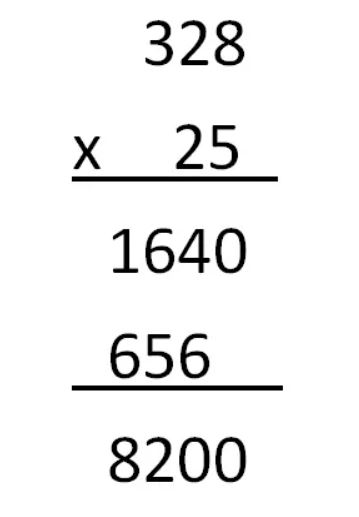
上图就是利用竖式进行乘法计算的过程：首先把数位较多的数写在上面，数位较少的数写在下面，然后上下数字的数位要对齐，然后将下面因数的个位数与上面因数的个位相乘，然后把它们积的末位写在个位上，再与十位上的数相乘写在十位上，以此类推。再对下面因数的十位数进行乘积运算，需要注意的是，此时与上面因数个位乘积的末位是对齐在乘数的十位下面，即此时 2 × 8 的末位 6 是对齐乘数 2 的。

# 具体事项请看代码注释

#include<iostream>
#include<cstring>
 
using namespace std;
 
int a[10001], b[10001], c[30000];          
//使用数组a、b存放待相乘的两个整数，使用数组c存放乘积后的结果
 
void ts(char *str, int *num, int len)       //将字符转化为整数
{
    int i, j;
    for(i = len - 1, j = 0; i >= 0; j++, i--)
    {
        num[j] = str[i] - '0';
    }
}
//由于从键盘中输入整数时，低位的数字都在字符数组的高地址区
//这里选择了将数位与下标的变化趋势一一对应，即个位数字--下标0，十位数字--下标1，以此类推
//所以乘积结果的最高位会在高地址区
 
void multiply(int *a, int *b, int *c, int len_a, int len_b)     //模拟竖式乘法计算的过程
{
    int i, j, temp;                 //使用变量temp记录每次的乘积
    for(i = 0; i < len_a; i++)
    {
        for(j = 0; j < len_b; j++)     //乘积的过程即，若满 10，则在该位留下对 10 的余数，再将大于 10 的部分进 1 位的操作
        {
            temp = a[i] * b[j];
            c[j + i + 1] = c[j + i + 1] + (c[j + i] + temp) / 10;  
            c[j + i] = (c[j + i] + temp) % 10;
        }
    }
    //为什么对乘积 c 的下标索引都加了i？
    //通过上面图示的案例，我们知道在进行竖式计算时
    //相乘出来的乘积的个位，总是与此时的乘数对齐
    //而每次的乘数就是a[i]，它的位数就是i，所以加上i之后，就可以使得乘积个位是与乘数对齐的
     
    int len = len_a + len_b;       
    //通过计算可以证明，位数分别为 x、y 的两个整数，它们乘积的位数一定不会超过 x + y
    //比如 99 与 999 相乘，它们乘积一定小于 99 与 1000的乘积，所以自然位数也一定不会超过 99000 的位数
    //这里是举例 两位数 和 三位数 乘积的最大位数，对于其他情况一样可证
      
    for(i = len; i >= 0; i--)  //找到乘积结果最高位的，即从最大位数开始递减，第一个不等于0的数的下标
    {
        if(c[i] != 0)          
        {
            break;
        }
    }
    for(j = i; j >= 0; j--)
    {
        printf("%d", c[j]);
    }
}
 
int main()
{
    int len_a, len_b;
    char M[10001], N[10001]; 
    //注意输入的两个整数就已经超过了整型的范围，所以这里要用字符串来读取输入，然后再进行转换
    scanf("%s", M);
    scanf("%s", N);
     
    len_a = strlen(M);
    len_b = strlen(N);
    ts(M, a, len_a);
    ts(N, b, len_b);

    if(len_a > len_b)   //这里使用判断语句，是为了保证将数位较少的放在竖式下面
    {
        multiply(b, a, c, len_b, len_a);
    }
    else
    {
        multiply(a, b, c, len_a, len_b);
    }
    return 0;
}