【题目】BZOJ-4987 Tree

题目大意

从前有棵树。找出$k$个点$A_1,A_2,\dots ,A_k$，使得$\sum _{i=1}^{k-1}dist(A_i,A_{i+1})$最小。

$1⩽N⩽3000$。

---

思路

题目要求的是从点$A_1$开始，依次经过$A_2,A_3,\dots$，最后到达$A_k$走过的最短路程。

首先，这$k$个点中任意两点之间一定不会有这$k$个点以外的点，否则把这个点纳入$k$个点内，得到的方案更优。于是这$k$个点构成了一棵大小为$k$的树，并且是原树的一部分。

其次，$A_1$到$A_k$这条路径上的边被经过一次，其余的边都被经过两次。可以通过画图验证。

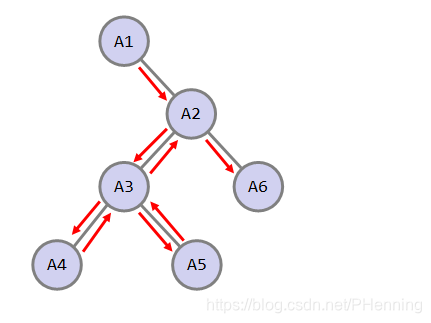
根据树形背包的套路，容易定出状态$f[u][i]$，表示从以$u$为根的子树中选出包含$u$的$i$个点对答案的贡献，然后把点$u$自身以外的$i-1$个点分配给每个儿子$v$。但是边$(u,v)$被经过的次数无法确定。

在状态后面添加一维$j$，表示选择的$i$个点中有$j$个点是$A_1$到$A_k$这条路径的端点（起点$A_1$或终点$A_k$）。$j$的范围是$[0,2]$。下面分情况讨论。

• $u$已讨论的部分子树和$v$的子树中都没有路径的端点，那么这条路径一定没有经过边$(u,v)$。这条边被经过了两次。
• $u$已讨论的部分子树中没有路径的端点，而$v$的子树中有一个，那么这条路径从$v$的子树内出发，经过边$(u,v)$，走到了已讨论的子树外的部分。这条边被经过了一次。
• $u$已讨论的部分子树中有一个路径的端点，而$v$的子树中没有，那么这条路径从$u$已讨论的子树内出发，没有进入$v$的子树内，说明路径没有经过边$(u,v)$。这条边被经过了两次。
• $u$已讨论的部分子树中没有路径的端点，而$v$的子树中有两个，那么这条路径被包含在$v$的子树内，没有经过边$(u,v)$。这条边被经过了两次。
• $u$已讨论的部分子树和$v$的子树各有一个端点，那么这条路径一定经过边$(u,v)$。这条边被经过了一次。
• $u$已讨论的部分子树中有两个路径的端点，而$v$的子树中没有，那么这条路径被包含在$u$已讨论的子树内，没有经过边$(u,v)$。这条边被经过了两次。

很好看的状态转移方程：

f[u][i+j][0]=min⁡{f[u][i][0]+f[v][j][0]+len(u,v)⋅2}f[u][i+j][1]=min⁡{f[u][i][0]+f[v][j][1]+len(u,v)f[u][i][1]+f[v][j][0]+len(u,v)⋅2f[u][i+j][2]=min⁡{f[u][i][0]+f[v][j][2]+len(u,v)⋅2f[u][i][1]+f[v][j][1]+len(u,v)f[u][i][2]+f[v][j][0]+len(u,v)⋅2\begin{aligned} f[u][i+j][0]&=\min\{f[u][i][0]+f[v][j][0]+len(u,v)\cdot 2\}\\ f[u][i+j][1]&=\min\begin{cases} f[u][i][0]+f[v][j][1]+len(u,v)\\ f[u][i][1]+f[v][j][0]+len(u,v)\cdot 2 \end{cases}\\ f[u][i+j][2]&=\min\begin{cases} f[u][i][0]+f[v][j][2]+len(u,v)\cdot 2\\ f[u][i][1]+f[v][j][1]+len(u,v)\\ f[u][i][2]+f[v][j][0]+len(u,v)\cdot 2 \end{cases} \end{aligned}f[u][i+j][0]f[u][i+j][1]f[u][i+j][2]​=min{f[u][i][0]+f[v][j][0]+len(u,v)⋅2}=min{f[u][i][0]+f[v][j][1]+len(u,v)f[u][i][1]+f[v][j][0]+len(u,v)⋅2​=min⎩⎪⎨⎪⎧​f[u][i][0]+f[v][j][2]+len(u,v)⋅2f[u][i][1]+f[v][j][1]+len(u,v)f[u][i][2]+f[v][j][0]+len(u,v)⋅2​​