CSU 2164 2018 组合数_csu - 2164-优快云博客

本文深入探讨了组合数的求解方法，通过分析和理解往届比赛题目，总结出利用组合数公式(C(n+m,n)-1)*(C(n+m,n)-1)%mod解决特定问题的策略。文章分享了作者在补题过程中的思考和学习，提供了AC代码示例，包括预处理逆元和组合数计算，以及详细的代码解释。

CSU 2164 2018 组合数

在省赛之前看看往届的题目,做题的时候有想到种类相乘,但是没有写...

补题的时候看了许多大佬的题解也没有完全理解

所以差不多理解了之后写一下博客

参考:https://blog.youkuaiyun.com/a465798176/article/details/89947130

https://blog.youkuaiyun.com/songziqi98/article/details/82528535

还有用找规律求解的

https://blog.youkuaiyun.com/qq_41061455/article/details/82890702

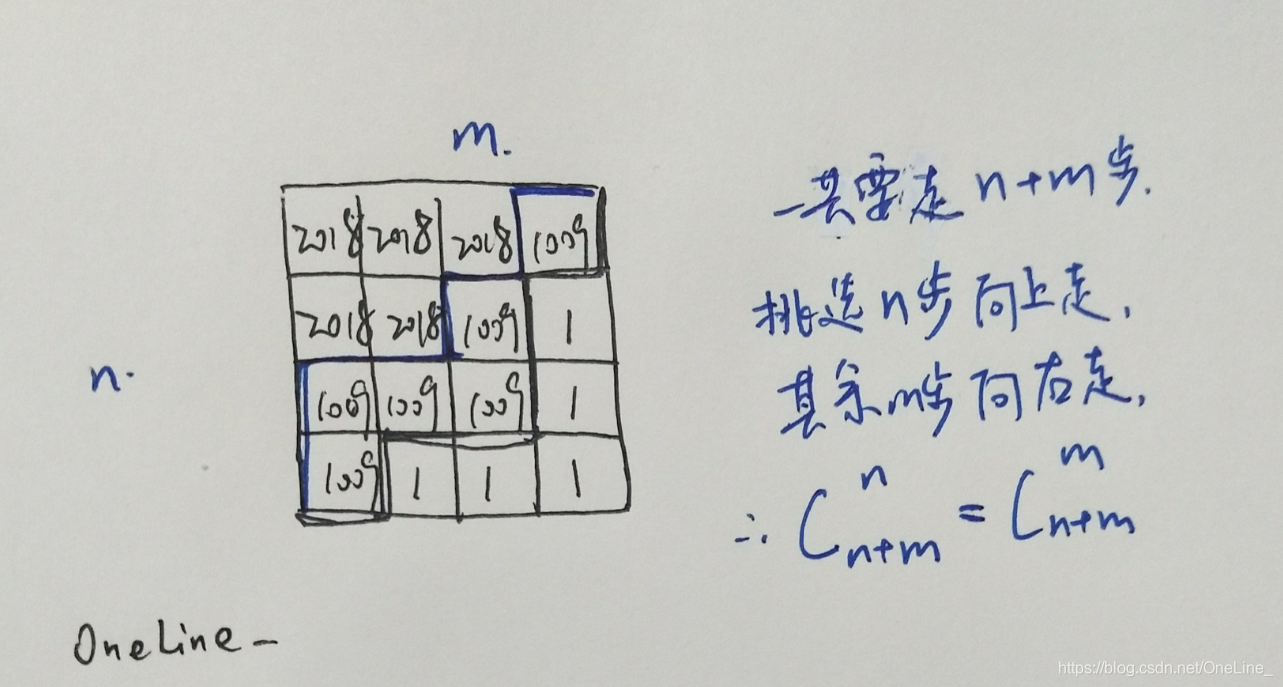
组合数得到答案的公式是 ( C(n+m,n)-1 )* ( C(n+m,n)-1 )%mod

AC代码

#include <stdio.h>
#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int mod  = 1e9 + 7;
const int inv2 = (mod + 1) / 2;
const int inv6 = (mod + 1) / 6;
ll sum[4005];
ll inv[4005];
ll res[4005];
void run()
{
    inv[1] = 1;
    sum[1] = 1;
    res[1] = inv[1];
    for (int i = 2; i <= 4005; i++) {
        inv[i] = (mod - mod / i) * inv[mod % i] % mod;
        res[i] = res[i - 1] * inv[i] % mod;
        sum[i] = sum[i - 1] * i % mod;
    }
}
ll C(int x, int y)
{
    ll ans = sum[x];
    return ans*res[y]%mod*res[x-y]%mod;
}
int main()
{
    run();
    int t, n, m;
    while (~scanf("%d%d", &n, &m)) {
        ll ans = C(n + m, m);
        ans = ((ans - 1 + mod) % mod * (ans - 1 + mod) % mod) % mod;
        printf("%lld\n", ans);
    }
    return 0;
}