前缀和与差分-优快云博客

一.前缀和

【定义】

前缀和是指某序列的前n项和，可以把它理解为数学上的数列的前n项和，而差分可以看成前缀和的逆运算。合理的使用前缀和与差分，可以将某些复杂的问题简单化（时间复杂度从O(n) / O(nm)到O( 1 ) ）。

如Si = a1+a2+a3+…ai; Si就是数列的前 i 项和

通过前缀和可以快速求出数组中某个区间的数值之和

【分析】

【代码】

#include <bits/stdc++.h>
using namespace std;
const int N=100010;
int a[N],f[N];
int main(){
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++) scanf("%d",&a[i]);
    for(int i=1;i<=n;i++) f[i]=f[i-1]+a[i];
    while(m--){//m个询问
        int l,r;
        scanf("%d%d",&l,&r);
        printf("%d\n",f[r]-f[l-1]);//输出前缀和
    }
    return 0;
}

例2 Acwing 子矩阵的和

【分析】

二维版，，，看图

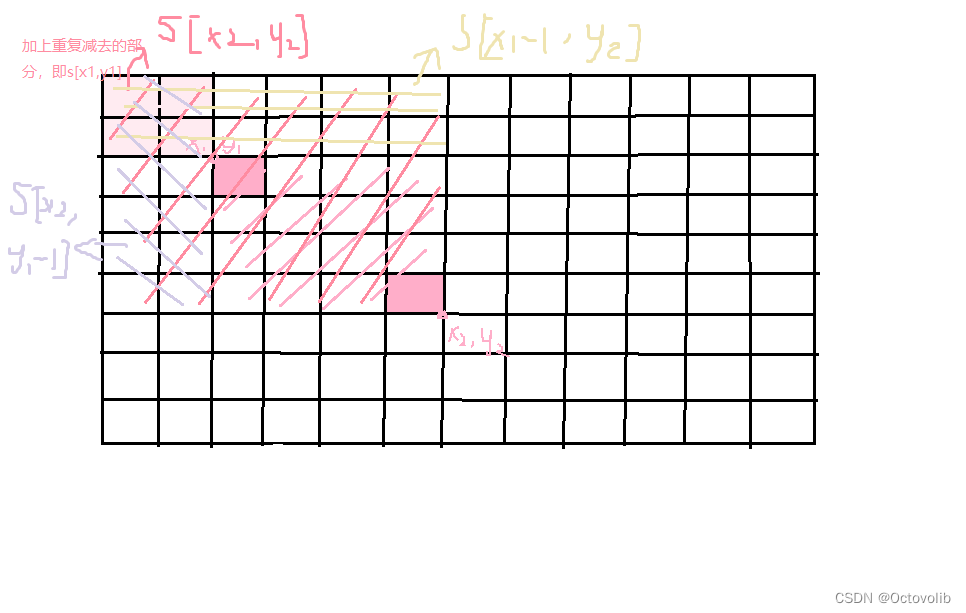
【代码】

#include <bits/stdc++.h>
using namespace std;
int s[1005][1005];
int n,m,q;
int main(){
    scanf("%d%d%d",&n,&m,&q);
    for(int i=1;i<=n;i++){
            for(int j=1;j<=m;j++){
                scanf("%d",&s[i][j]);
            }
        }
    for(int i=1;i<=n;i++){
            for(int j=1;j<=m;j++){
                s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+s[i][j];
            }
        }
    while(q--){
        int x1,y1,x2,y2;
        scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
        printf("%d\n",s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);
    }
    return 0;
}

二.差分

对于原数组a[1],a[2],a[3],...,a[n]，我们假想一个b数组，满足b[1]+b[2]+b[3]+...+b[n]=a[n]，即a数组为b数组的前缀和，那么称b数组为差分数组。可以将差分看作前缀和的逆运算。

a[0]=0

b[1]=a[1]-a[0]

b[2]=a[2]-a[1]

b[3]=a[=3]-a[2]

b[n]=a[n]-a[n-1]

由上可得b[1]+b[2]+b[3]+...+b[n]=a[n]

例1 Acwing 差分

【分析】

要使原数组中给定区间的每一个元素都加上c，可使其差分数组中每个元素+c，原数组自然而然地实现了这一操作。此外要注意区间外的数+c后还需减去（因为useless），并用到插入函数。

【代码】

#include <bits/stdc++.h>
using namespace std;
const int N=1000010;
int a[N],b[N];//a为原数组，b为差分数组
int n,m;
void insert(int l,int r,int c ){
    b[l]+=c;
    b[r+1]-=c;
}//插入函数，令b[l]后的每一个数都加上c，b[r+1]后的每一个数减c（区间外不需要处理）
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        scanf("%d",&a[i]);
        insert(i,i,a[i]);//a[i]初始为0，用函数插入数据
    }
    while(m--){
        int l,r,c;
        scanf("%d%d%d",&l,&r,&c);
        insert(l,r,c);
    }
    for(int i=1;i<=n;i++){
        b[i]+=b[i-1];
    }//令b数组等于它本身的前缀和
    for(int i=1;i<=n;i++) printf("%d ",b[i]);
    return 0;
}

例2 Acwing 差分矩阵

【分析】

二维版again，，，大概模板和上面差不多，除了结论的推理。

【代码】

#include <bits/stdc++.h>
using namespace std;
const int N=1010;
int a[N][N],b[N][N];
int n,m,q;
void insert(int x1,int y1,int x2,int y2,int c){
    b[x1][y1]+=c;
    b[x2+1][y1]-=c;
    b[x1][y2+1]-=c;
    b[x2+1][y2+1]+=c;
}
int main(){
    cin>>n>>m>>q;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            scanf("%d",&a[i][j]);
            insert(i,j,i,j,a[i][j]);
        }
    }
    while(q--){
        int x1,y1,x2,y2,c;
        cin>>x1>>y1>>x2>>y2>>c;
        insert(x1,y1,x2,y2,c);
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            b[i][j]+=b[i-1][j]+b[i][j-1]-b[i-1][j-1];
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            printf("%d ",b[i][j]);
        }
        cout<<endl;
    }
    return 0;
}