图的遍历^-^_深度优先遍历算法中^是什么意思-优快云博客

【邻接表】

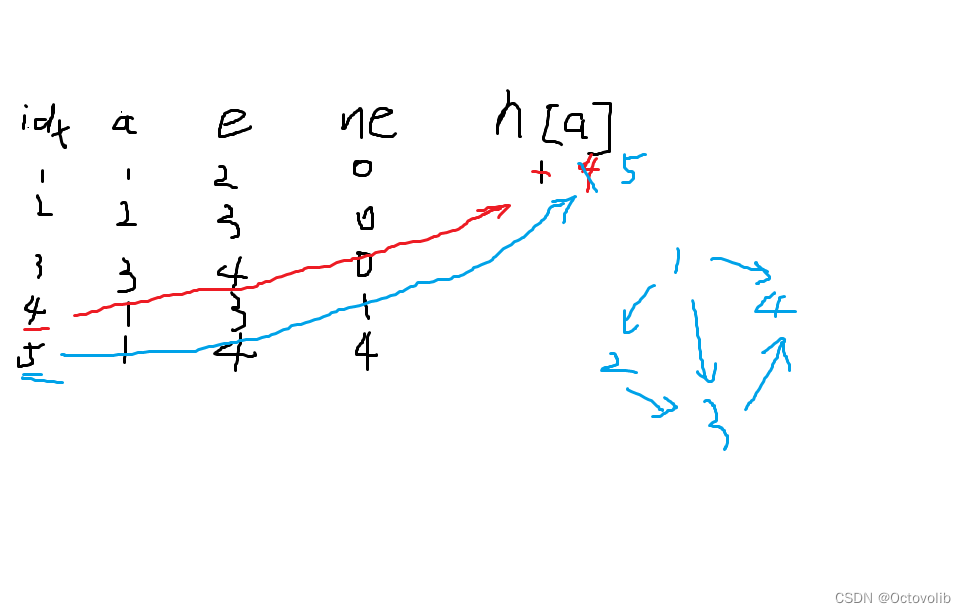
看图回忆

一定要记住

e[idx]=b;
ne[idx]=h[a];
h[a]=idx++;

2.for(int i=h[idx];i!=0;i=ne[idx])

【定义】

从给定图中任意指定的顶点（称为初始点）出发，按照某种搜索方法沿着图的边访问图中所有顶点，使每个顶点仅被访问一次，这个过程称为图的遍历。如果给定图是连通的无向图或者是强连通的有向图，则遍历过程一次就能完成，并可按访问的先后顺序得到由该图的所有顶点组成的一个序列。

【方法】

1.深度优先遍历

2.广度优先遍历

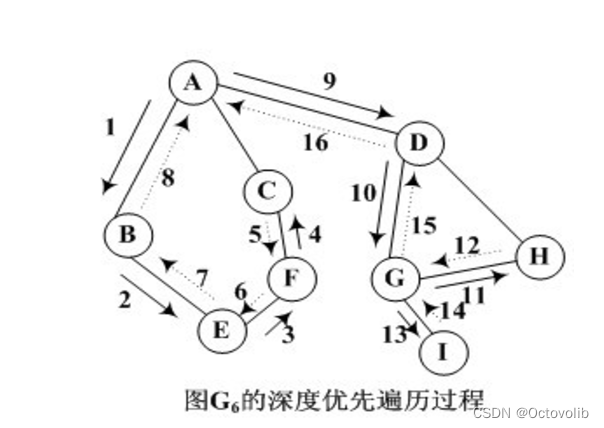
深度优先搜索

深度优先遍历的过程是从图中的某个初始点v出发，首先访问初始点v，然后选择一个与顶点v相邻且没被访问过的顶点w，以w为初始顶点，再从它出发进行深度优先遍历，直到图中与顶点v邻接的所有顶点都被访问为止，显然这是一个递归过程。

例题 OJ341 一笔画问题

【分析】

1.首先需要理解欧拉路和欧拉回路，这两种图都是连通的，而欧拉回路没有奇点。

2.图中寻找奇点，如果有奇点，说明为欧拉路，需从奇点开始搜索；否则，可从任意点开始。因而可将st赋初值为1。

【代码】

#include <bits/stdc++.h>
using namespace std;
int f[1005][1005];//f用来存储图 
int a[1005],d[1005];//a存路径，d存各点的度 
int n,m,idx=0;
void dfs(int st){
	for(int i=1;i<=n;i++){
		if(f[st][i]==1){//如果两点间有边 
			f[st][i]=0;
			f[i][st]=0;//抹去 
			dfs(i);//继续搜索 
		}
	}
	a[++idx]=st;//拓展路径 
}
int main(){
	memset(f,0,sizeof(f)); 
	cin>>n>>m;
	int x,y;
	for(int i=1;i<=m;i++){
		scanf("%d%d",&x,&y);
		f[x][y]=1;
		f[y][x]=1;//双向图，两点间有边 
		d[x]++;
		d[y]++;//两点的度数都++ 
	}
	int st=1;
	for(int i=1;i<=n;i++){
		if(d[i]%2==1){//找到奇点 
			st=i;
			break;
		}
	}
	dfs(st);//开始搜索 
	for(int i=1;i<=idx;i++){
		cout<<a[i]<<" ";
	}
	return 0;
}

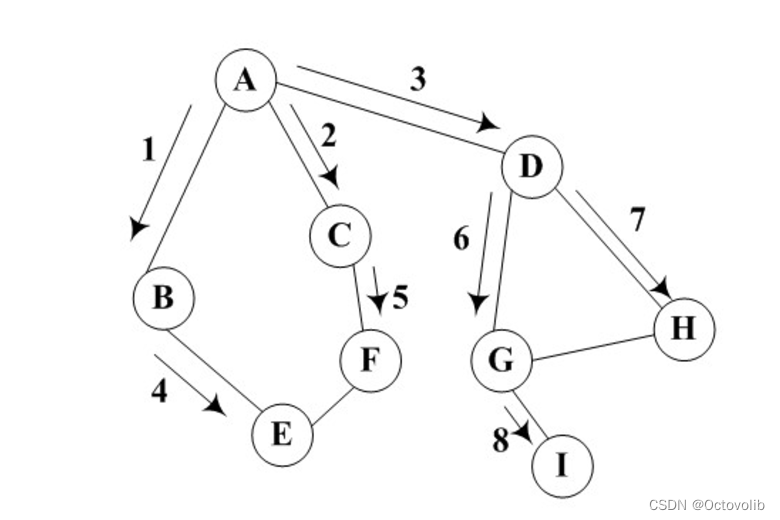
广度优先搜索

广度优先遍历的过程是首先访问初始点v，接着访问顶点v的所有未被访问过的邻接点v1，v2，v3，…，vt，然后再按照v1，v2，v3，…，vt的次序访问每一个顶点的所有未被访问过的邻接点，依此类推，直到图中所有和初始点v有路径相通的顶点都被访问过为止。为了实现先访问顶点的邻接顶点先访问，需要借用队列来实现。
————————————————
版权声明：本文为优快云博主「红心火柴」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.youkuaiyun.com/qq_44075108/article/details/116222906

例题 Acwing 图中点的层次

【分析】

1.求最短距离，先想到广搜。

2.将数据用邻接表存储，因为要从顶点开始，需用到队列。

3.c数组用来存储路径长，b数组用来标记访问过的点。因此用b标记初始点为1，而此时距离为0

4.然后开始搜索，注意后面到达的点的路径长需要承接上一个点并加1

5.记得处理不能到达n点的情况（即该点没有被标记）

【代码】

#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int e[N],ne[N],h[N],b[N],c[N];//c用来存储路径
int n,m,x,y,idx=1;//idx记得要赋初值为1
void add(int x,int y){
    e[idx]=y;
    ne[idx]=h[x];
    h[x]=idx++;
}//存储
queue<int> q;
void bfs(int x){
    q.push(x);//将x点放进队列
    b[x]=1;//标记用过的点
    c[x]=0;//刚开始路径为0
    while(q.size()){
        int t;
        t=q.front();
        q.pop();
        for(int i=h[t];i!=0;i=ne[i]){
            int kt;
            kt=e[i];//kt为从t点出发到达的下一个点
            if(b[kt]==1) continue;//用过的点pass
            q.push(kt);//keep going
            b[kt]=1;//标记 
            c[kt]=c[t]+1;//到达kt的路径长为出发点t时的路径长加一
        }
    }
}
int main(){
    cin>>n>>m;
    for(int i=1;i<=m;i++){
        scanf("%d%d",&x,&y);
        add(x,y);//存入数据
    }
    bfs(1);//从第一个点开始搜索
    if(b[n]==0) cout<<"-1";//不能到达n点（即n点未被标记）
    else cout<<c[n];
    return 0;
}