NumPy 广播机制简介

       在 Python 的科学计算领域，NumPy 库无疑占据着举足轻重的地位。它提供了高效的多维数组操作功能，极大地简化了数据处理与分析的过程。其中，广播（Broadcasting）机制是 NumPy 中一个强大且实用的特性，今天就带大家了解一下。​

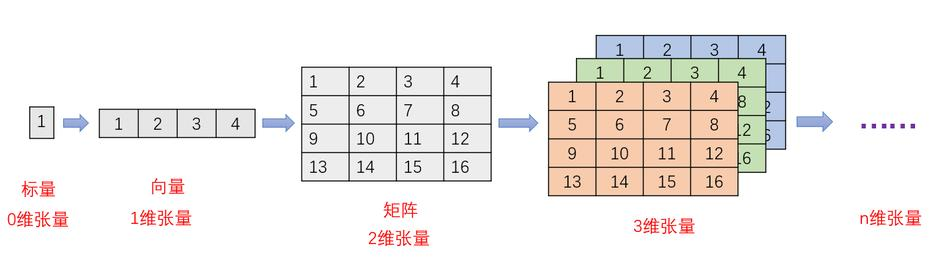
什么是广播机制​

      在日常的数组运算中，我们常常期望对不同形状的数组执行算术运算。例如，将一个标量（单个数值）加到一个数组的每个元素上，或者将一个一维数组与一个二维数组按特定规则进行运算。传统情况下，如果数组形状不匹配，直接运算会报错。但 NumPy 的广播机制打破了这一限制，它允许在一定规则下，对形状不同的数组进行元素级别的运算，而无需手动将数组形状调整一致。这种机制通过虚拟扩展较小数组的形状，使其与较大数组兼容，从而实现高效的运算，并且不会在内存中真正复制数据，节省了内存空间。​

广播机制的规则​

   规则一：维度补齐​

当参与运算的两个数组维度不同时，NumPy 会在维度较少的数组前面添加长度为 1 的维度，直到两个数组的维度数量相同。例如，一个形状为 (3,) 的一维数组与一个形状为 (2, 3, 4) 的三维数组运算时，一维数组会被 “视为” 形状为 (1, 1, 3) 的三维数组，这样两个数组的维度就一致了，均为三维。​

    规则二：形状匹配​

在维度数量相同后，从后向前逐个比较两个数组对应维度的大小。对于每个维度，若满足以下两种情况之一，则这两个数组在该维度上是兼容的：​

1. 两个数组在该维度的大小相等。​

1. 其中一个数组在该维度的大小为 1 。​

   比如，有数组 A 形状为 (2, 3, 4)，数组 B 形状为 (2, 1, 4)。从后往前看，第三维都是 4（相等），第二维一个是 3，一个是 1（满足其中一个为 1），第一维都是 2（相等），所以这两个数组在各个维度上都兼容，可以进行广播运算。若不满足上述条件，如数组 A 形状为 (2, 3, 4)，数组 B 形状为 (2, 5, 4)，第二维 3 和 5 既不相等，也没有一个为 1，此时广播就会失败，NumPy 会抛出ValueError错误。​

    规则三：维度扩展​

对于兼容的维度，若其中一个数组的维度大小为 1，会将该维度扩展为另一个数组对应维度的大小，以实现形状完全匹配。例如，数组 A 形状为 (2, 1, 3)，数组 B 形状为 (2, 4, 3)，在第二维上，A 的大小为 1，B 的大小为 4，因此 A 的第二维会被扩展为 4，最终两者形状都变为 (2, 4, 3)，进而进行元素级运算。​

广播机制的应用场景​

数组与标量的运算​

这是广播机制最常见的应用之一。当我们用一个标量去加一个数组时，标量会被广播成与数组相同形状的 “虚拟数组”，然后进行元素级加法。

输出为：[6 7 8 9]，这里标量 5 被广播成了与arr形状相同的数组[5, 5, 5, 5]，再与arr相加。​

不同维度数组的运算​

在处理高维数组时，广播机制能极大简化对某些维度进行统一操作的代码。例如，对一个二维数组的每一列进行标准化（减去列均值，除以列标准差）：​

这里，col_means和col_stds是形状为 (3,) 的一维数组，与形状为 (3, 3) 的arr进行运算时，会被广播成 (3, 3) 的数组，从而实现逐列标准化。​

生成网格数据​

在绘制二维函数图像等场景中，常需要生成网格数据，广播机制可轻松实现。将x和y分别扩展为二维网格。​

总结​

NumPy 的广播机制是其灵活性与高效性的重要体现，它允许不同形状的数组进行元素级运算，大大简化了数据处理代码。通过遵循维度扩展、形状匹配和维度扩展为匹配大小这三条核心规则，我们能判断两个数组是否可广播，并借此实现标量与数组、不同维度数组之间的各种操作，在数据科学、机器学习、图像处理等众多领域发挥着关键作用 。