线性代数：空间的基

最新推荐文章于 2025-01-05 14:39:49 发布

倪桦

最新推荐文章于 2025-01-05 14:39:49 发布

阅读量1k

点赞数 22

CC 4.0 BY-SA版权

分类专栏：线性代数文章标签：线性代数

本文链接：https://blog.youkuaiyun.com/Nh_code/article/details/143971182

线性代数专栏收录该内容

38 篇文章

订阅专栏

1、空间的基的概念

若 $m$ 个向量生成 $n$ 维 $v⃗m\vec v_{1},\ \vec v_{2},\ \vec v_{3},\cdots,\ \vec v_{m}$ 空间， $m$ 最小是为 $n$ ；
若 $m > n$ ，则 $v⃗m\vec v_{1},\ \vec v_{2},\ \vec v_{3},\cdots,\ \vec v_{m}$ 线性相关；
若 $m$ 个 $n$ 维向量线性无关， $m$ 最大为 $n$ 。
$理解线性无关:\color {skyblue} { \small理解线性无关:}$
$km⋅v⃗m=0⇔转而判断m个n维向量组成的系数矩阵A⋅k⃗=0有唯一零解\color {skyblue} {\small 求证线性无关等价于求证是否存在一组全为的系数k,使得k_{1} \cdot \vec v_{1} + \ k_{2} \cdot \vec v_{2} + \ k_{3} \cdot \vec v_{3} + \cdots + \ k_{m} \cdot \vec v_{m} = 0\Leftrightarrow 转而判断m个n维向量组成的系数矩阵 A \cdot \vec k = 0 有唯一零解}$
$m个不共线的n维向量组成的线性系统A⋅k⃗=0，是一个方程数大于未知数的线性系统，且行阶梯式的非零行个数等于未知数个数，所以有唯一零解，证得m个(m<n)个n维向量线性无关\color {skyblue} { \small m个不共线的n维向量组成的线性系统A\cdot \vec k =0，是一个方程数大于未知数的线性系统，且行阶梯式的非零行个数等于未知数个数，所以有唯一零解，证得m个(m < n)个n维向量线性无关}$

若一组向量可以生成整个 $n$ 维空间，且线性无关，这组向量一定有 $n$ 个，则称这组向量为这个 $n$ 维空间的一组 $基(bases)\color {red} {基(bases)}$

因为可以生成整个 $n$ 维空间的 $n$ 个线性无关的 $n$ 维向量可以有无数组，所以一个空间可以有无数组基。

从一个低维空间–二维空间来看待空间的基

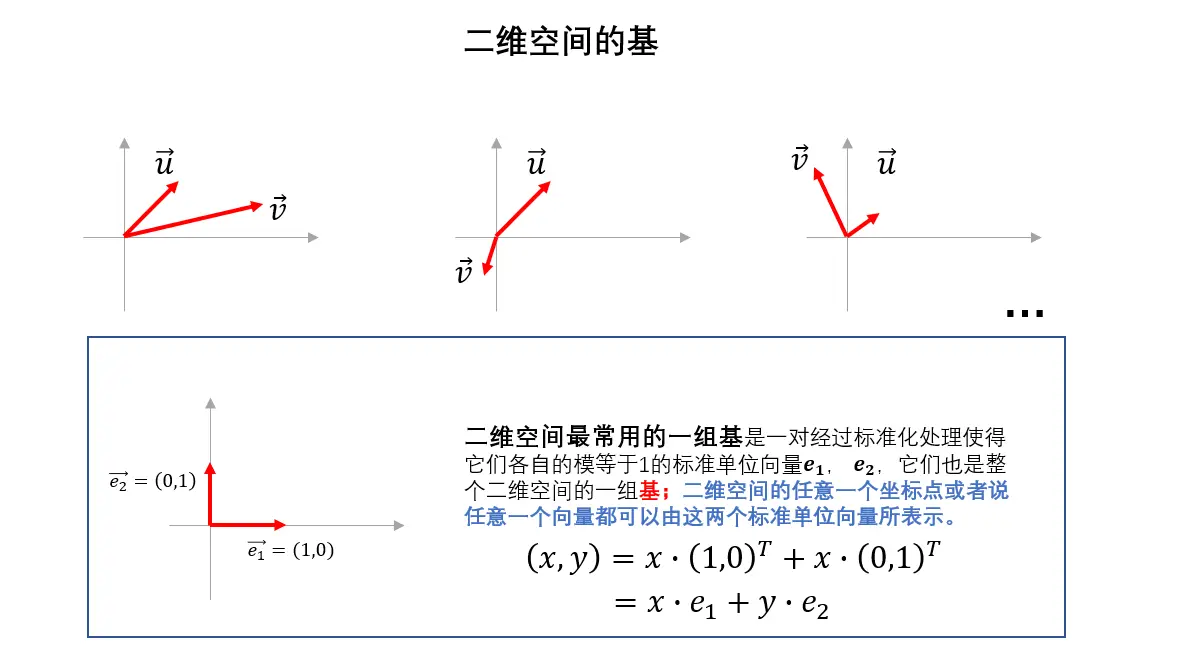
在二维空间中，任取两个不共线的向量 $u⃗\vec u$ 和 $v⃗\vec v$ ，它们就是二维空间的一组基，任意第三个向量都可以表示为 $u⃗\vec u$ 和 $v⃗\vec v$ 的线性组合。

基可以理解为一个初等数学接触的坐标系概念， $e⃗1，e⃗2\vec e_{1}，\vec e_{2}$ 是二维空间一组坐标系， $u⃗，v⃗\vec u，\vec v$ 也是一组坐标系，在这些坐标系下都可以观测到二维空间的任意一个点，区别在于不同的坐标系空间中同一个点的表示方式是不一样的。

给定 $n$ 维空间的一组基，则空间中的任意一个向量都可以表示成这组基的线性组合，且这个向量在这组基下的表示方法唯一。

证明：对 $n$ 维空间中的任意一个向量 $u⃗\vec u$ ，求证是否一定存在一组 $k$ ，使得：
$k1⋅e⃗1+k2⋅e⃗2+⋯+kn⋅e⃗n=u⃗k_{1} \cdot \vec e_{1} + k_{2} \cdot \vec e_{2} + \cdots + k_{n} \cdot \vec e_{n} = \vec u$
等价于求解线性系统: $[k1k2⋯kn]=[u1u2⋯un]\begin {bmatrix}1&0&\cdots 0\\ 0&1&\cdots 0 \\ \cdots& \cdots&\ \cdots \\ 0&0&\cdots 1 \end {bmatrix} \ \begin {bmatrix} k_{1} \\ k_{2} \\ \cdots \\ k_{n} \end {bmatrix}= \begin {bmatrix} u_{1} \\ u_{2} \\ \cdots \\ u_{n} \end {bmatrix}$
对于这个线性系统，系数矩阵 $A$ 一定可逆，所以一定有解，且有唯一解 $\cdot x =b \to x = A^{-1} \cdot b)$

2、空间的基的性质

n维空间中，任意n个线性无关的向量，一定是这个n维空间的基；
n维空间中，额如果n个向量可以生成整个空间，则这n个向量，是这个n维空间的基；
如果一组向量 $,v⃗p\vec v_{1},\vec v_{2},\cdots ,\vec v_{p}$ 可以生成 $n$ 维空间 $\geq n)$ ，则这组向量的存在一个子集，是 $n$ 维空间的一组基。— 该结论表明，很多时候，我们并不需要构造 $n$ 维空间的一组基如果，当存在 $p$ 个向量可以生成整个 $n$ 维空间的时候，只需要从这组向量里挑选出一个包含 $n$ 个线性无关向量的子集就可以成为这个 $n$ 维空间的一组基

对于 $m$ 个线性无关的 $n$ 维向量，若 $m < n$ ，这 $m$ 个向量无法生成整个空间；降低到三维空间来理解就是，如果只给出两个三维空间的向量 $v⃗\vec u,\ \vec v$ ，它们只能形成一个平面，则这两个向量的任意线性组合都在平面上，无法生成不在平面的向量。当 $m = n$ 时， $m$ 个线性无关的 $n$ 维向量可以生成整个空间，且可以成为空间的基。当 $m > n$ ，此时这 $m$ 个向量变成线性相关组，可以生成整个空间但不是空间的基。