线性代数：生成空间-优快云博客

若在二维空间中任何向量，都可以表示为 $u⃗\vec u$ 和 $v⃗\vec v$ 的线性组合，则可以说 $u⃗\vec u$ 和 $v⃗\vec v$ 生成整个二维空间。

在 $u⃗，v⃗\vec u， \vec v$ 生成的二维空间中，如加入一个向量 $m$ ，那么向量组 $u⃗，v⃗，m⃗\vec u， \vec v， \vec m$ 也可以生成整个二维空间，这个二维空间中，任意一个向量都可以表示为这三个向量的线性组合。由于向量组 $u⃗，v⃗\vec u， \vec v$ 已经生成了整个二维空间，那么空间内任意一个向量都可以由 $u⃗，v⃗\vec u， \vec v$ 的线性组合所表示，当向量 $m⃗\vec m$ 加入进来之后，只要向量 $m⃗\vec m$ 的组合常数 $k$ 取零，那么 $u⃗，v⃗，m⃗\vec u， \vec v， \vec m$ 三个向量的线性组合就可以表示任意一个向量，所以说 $u⃗，v⃗，m⃗\vec u， \vec v， \vec m$ 生成整个二维空间。

生成一个二维空间，至少需要两个向量。

如果只有一个向量，如向量 $v⃗\vec v$ ，通过一个向量 $v⃗\vec v$ 的线性组合获得的向量一定在 $v⃗\vec v$ 向量所在的直线上，因为一个向量前面乘以一个系数 $k$ 本质只是在对向量进行缩放。所以一个向量无法生成一个二维的面。
最少肯定也不是3个向量，因为如果已经存在两个向量不共线，那么这第三个向量就可以由前两个向量的线性组合所表示，在这种情况下，第三个向量就已经是多余的了。

推广到空间中，若空间中的任一向量都可以表示成 $v⃗p\vec v_{1},\ \vec v_{2},\ \vec v_{3},\cdots,\ \vec v_{p}$ 的线性组合，则称这些向量可以生成这个空间。 要生成一个 $n$ 维空间，至少需要 $n$ 个向量才能够生成。其中，对于 $n$ 个向量，若这 $n$ 个向量存在共线向量，是不可以生成 $n$ 维空间的。

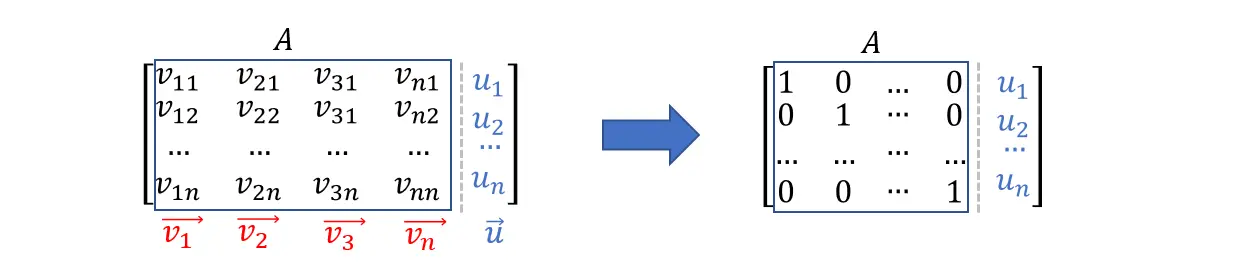
证明：当且仅当由 $n$ 个 $n$ 维向量的列向量组成的方阵A有逆的时候，可以生成整个 $n$ 维空间。
若 $n$ 个 $n$ 维向量 $v⃗\vec v$ 生成整个空间，那么对于这 $n$ 个向量 $v⃗\vec v$ 的列向量组成的系数矩阵 $A$ 与 $n$ 维空间中的任意一个向量 $u⃗\vec u$ 组成的线性系统是一定有解的，也就是 $n$ 维空间里的任意向量都可以由生成空间的 $n$ 个 $n$ 维 $v⃗\vec v$ 向量的一个唯一线性组合表示。由于 $u⃗\vec u$ 是空间中任意一个向量，所以向量 $u⃗\vec u$ 的分量是随机的( $u_{i}$ 可能为是一个非零数)，因此线性系统的系数矩阵 $A$ 的行最简形式一定不能存在零行，若存在零行，那么矩阵 $A$ 无解，向量组 $v⃗\vec v$ 的线性组合无法表示空间内的向量 $u⃗\vec u$ 。
既然系数矩阵 $A$ 的行最简式都是非零行,那么线性系统满足 $n$ 个未知数和 $n$ 个方程，所以线性系统不可能有无穷解，只有有唯一非零解。此时当一个线性系统只有唯一解的时候，意味着对应的增广矩阵的系数矩阵 $A$ 一定是可逆的，因为只有可逆矩阵满足 $\to x= A^{-1}b$ 。