线性代数：矩阵与空间_欧拉空间定义-优快云博客

本文链接：https://blog.youkuaiyun.com/Nh_code/article/details/143968365

标准空间：欧拉空间是对现实空间的规则抽象和推广（从n<=3推广到有限n维空间）。
一个标准二维空间由互相垂直的两个标准单位向量 $e⃗2=(0,1)\vec e_1=(1,0) 和 \ \vec e_2=(0,1)$ 所定义，在 $e⃗1\vec e_1$ 向量方向上的移动单位为 $e⃗1\vec e_1$ 向量的模 $∥e⃗1∥\|\vec e_1\|$ ，在 $e⃗2\vec e_2$ 向量方向上的移动单位为 $e⃗2\vec e_2$ 向量的模 $∥e⃗2∥\|\vec e_2\|$ 。用矩阵表示这个二维空间：

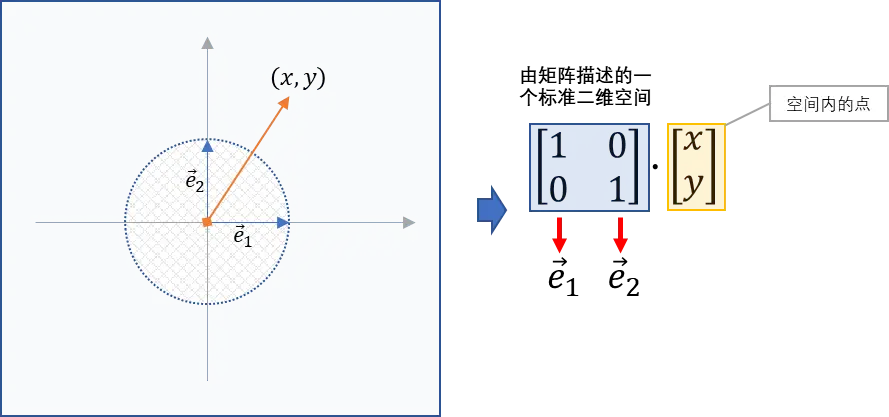
从列视角看待下式矩阵与向量的乘法：
$[1001]⋅[xy]=[10]x+[01]y=[x0]+[0y]=[xy]=x⋅e⃗1+y⋅e⃗2\begin{bmatrix} 1&0 \\ 0&1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 1\\0\end{bmatrix}x + \begin{bmatrix} 0 \\1 \end{bmatrix}y = \begin{bmatrix} x \\0 \end{bmatrix} + \begin{bmatrix} 0\\y \end{bmatrix} = \begin{bmatrix} x \\y \end{bmatrix} = x \cdot \vec e_1 + y \cdot \vec e_2$
在 $e⃗2=(0,1)\vec e_1=(1,0)和 \ \vec e_2=(0,1)$ 所定义的空间中， $(x, y)$ 这个坐标释意为描述一个在 $e⃗1\vec e_1$ 向量方向上的移动单位为 $\cdot \|\vec e_1\|$ ，和在 $e⃗2\vec e_2$ 向量方向上移动 $y$ 个$ |\vec e_2| $单位后的点。构成空间的两个向量的模都是 1 ，所以在两向量中分别移动$ x,y $单位后的结果向量在该空间中为描述$ (x,y)$。

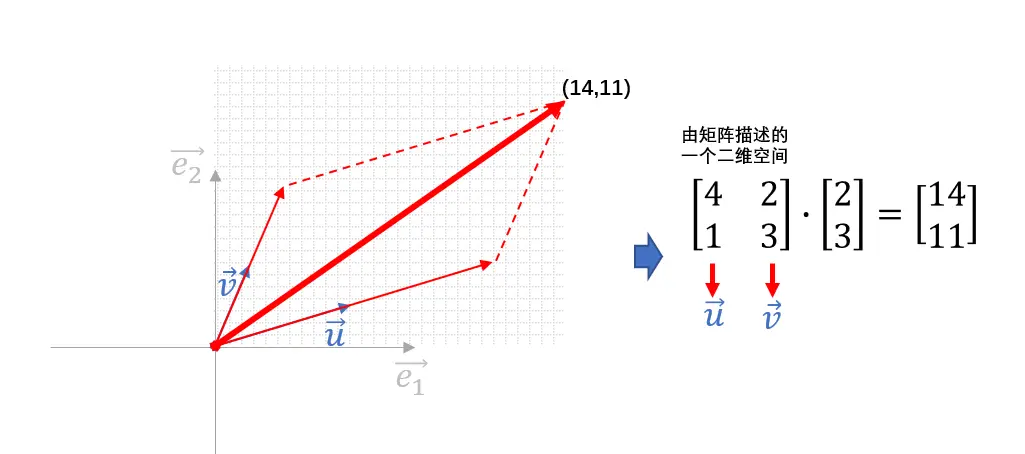
在欧拉空间中，任意 $n$ 个线性无关向量组都可以建立一个空间，如两线性无关向量 $v⃗\vec u \ , \ \vec v$ 建立了一个空间: $[4213]\begin{bmatrix} 4&2 \\ 1&3 \end{bmatrix}$ ， $v⃗两向量的分量值是基于标准欧式空间给出的描述\color{red}{ \small 其中}\color{red}{\vec u \ , \ \vec v} \color{red}{\small 两向量的分量值是基于标准欧式空间给出的描述}$ 。我们可以知道，一个标准二维空间的点 $(2, 3)$ ，坐标 $(2, 3)$ 是在这个标准二维空间中 $e⃗1\vec e_1$ 方向上移动2个单位， $e⃗2\vec e_2$ 方向上移动3个单位的点对象的位置描述，这个点在 $v⃗\vec u \ , \ \vec v$ 建立的空间体系中的描述坐标应该是：
$[4213]⋅[23]=2⋅[41]+3⋅[23]=[1411]=2⋅u⃗+2⋅v⃗\begin{bmatrix} 4&2 \\ 1&3 \end{bmatrix} \cdot \begin{bmatrix} 2 \\ 3\end{bmatrix} = 2 \cdot \begin{bmatrix} 4\\1\end{bmatrix} + 3 \cdot \begin{bmatrix} 2 \\ 3 \end{bmatrix} = \begin{bmatrix} 14 \\ 11 \end{bmatrix} = 2 \cdot \vec u + 2 \cdot \vec v$