智能机器人与旋量代数(12)

最新推荐文章于 2025-07-13 15:08:21 发布

原创

最新推荐文章于 2025-07-13 15:08:21 发布 · 4k 阅读

34 ·

CC 4.0 BY-SA版权

文章标签：

#机器人

Chapt 4. 旋量代数在机器人学中的应用

4.1 串联机器人正运动学的指数积(PoE, Product of Exponetial)公式

4.1.1 回顾：机器人正运动学的Denavit-Hartenberg (D-H)参数公式

D-H 建模法: D-H 建模方法是由 Denavit 和 Hartenberg (ASME, 1955) 提出的一种建模方法，主要用在机器人运动学上。此方法在机器人的每个连杆上建立一个坐标系，通过齐次坐标变换实现两个连杆上的坐标变换，建立多连杆串联系统中首末坐标系的变换关系。
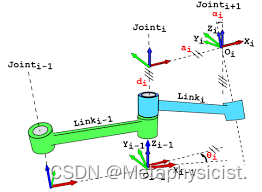
在这里插入图片描述

D-H 建模方法的几个要点如下：

a. 建立连杆坐标系；

b.确定四个参数 $α\alpha$ , $a$ , $d$ , $θ\theta$ ；

c. 列D-H参数表；

d.由参数表得到变换矩阵；

D-H 建模方法中，每个连杆使用 4 个参数 $α\alpha$ , $a$ , $d$ , $θ\theta$ 来描述，2 个描述连杆本身，另外 2 个描述与相邻连杆的位姿（连接或几何关系）。

对于转动关节，其中 $θ\theta$ 为关节变量，其他三个参数固定不变，为连杆参数；对于移动关节， $d$ 为关节变量，其他三个为关节参数。

根据连杆坐标系和关节对应关系的不同，D-H 建模法可以分为传统 D-H (Classic DH) 和改进 D-H (Modified DH)，二者的主要区别如下表所示。

区别	Classic D-H	Modified D-H
连杆固定坐标系的位置	后一个关节坐标系	前一个关节坐标系
$X$ 轴的确定方式	当前坐标系 $Z$ 轴和前一个坐标系 $Z$ 轴的向量积	后一个坐标系 $Z$ 轴与当前坐标系 $Z$ 轴的向量积
坐标系间的参数变换顺序	$θ\theta$ , $d$ , $a$ , $α\alpha$	$α\alpha$ , $a$ , $θ\theta$ , $d$

Classic D-H:

Classic DH 的关节和坐标系关系中各个参数的含义如下：

$θi\theta_{i}$ : $X_{i-1}$ 到 $X_{i}$ 绕 $Z_{i-1}$ 旋转的角度；

$d_{i}$ : $X_{i-1}$ 到 $X_{i}$ 沿 $Z_{i-1}$ 方向的距离；

$a_{i}$ ： $Z_{i-1}$ 到 $Z_{i}$ 沿 $X_{i-1}$ 方向的距离；

$αi\alpha_{i}$ : $Z_{i-1}$ 到 $Z_{i}$ 绕 $X_{i-1}$ 旋转的角度

坐标系 $O_{i-1}$ 与关节 $i$ 对齐，其 D-H 参数矩阵为：

$_{i}^{i-1}T = \begin{bmatrix} \cos{\theta_{i}} & -\sin{\theta_{i}} \cos{\alpha_{i}} & \sin{\theta_{i}} \sin{\alpha_{i}} & a_{i} \cos{\theta_{i}} \\ \sin{\theta_{i}} & \cos{\theta_{i}} \cos{\alpha_{i}} & -\cos{\theta_{i}} \sin{\alpha_{i}} & a_{i} \sin{\theta_{i}} \\ 0 & \sin{\alpha_{i}} & \cos{\alpha_{i}} & d_{i} \\ 0 & 0 & 0 & 1 \end{bmatrix}$

Modified DH:

Modified D-H 的关节和坐标系关系中各个参数的含义如下：

$αi−1\alpha_{i-1}$ ： $Z_{i-1}$ 到 $Z_{i}$ 绕 $X_{i-1}$ 旋转的角度；

$a_{i-1}$ ： $Z_{i-1}$ 到 $Z_{i}$ 沿 $X_{i-1}$ 方向的距离；

$θi\theta_{i}$ ： $X_{i-1}$ 到 $X_{i}$ 绕 $Z_{i}$ 旋转的角度；

$d_{i}$ ： $X_{i-1}$ 到 $X_{i}$ 沿 $Z_{i}$ 方向的距离。

坐标系 $O_{i-1}$ 与关节 $i - 1$ 对齐，其 D-H 参数矩阵为：
在这里插入图片描述

$_{i}^{i-1}T = \begin{bmatrix} \cos{\theta_{i}} & -\sin{\theta_{i}} & 0 & a_{i-1} \\ \sin{\theta_{i}} \cos{\alpha_{i-1}} & \cos{\theta_{i}} \cos{\alpha_{i-1}} & -\sin{\alpha_{i-1}} & -d_{i} \sin{\alpha_{i-1}} \\ \sin{\theta_{i}} \sin{\alpha_{i-1}} &\cos{\theta_{i}} \sin{\alpha_{i-1}} & \cos{\alpha_{i-1}} & d_{i} \cos{\alpha_{i-1}} \\ 0 & 0 & 0 & 1 \end{bmatrix}$