【优化求解】果蝇优化算法

文章目录

• 一、理论基础
• 二、算法步骤
• • 1、启发
  • 2、方向和距离
  • 3、气味浓度判断值
  • 4、适应度评估
  • 5、寻找最优个体
  • 6、飞行
  • 7、迭代优化
• 三、案例背景
• • 问题描述
• 四、MATLAB程序实现
• • 1、清空环境变量
  • 2、初始化参数
  • 3、寻找初始最优
  • 4、迭代寻优
  • 5、结果显示
  • 6、绘图
• 五、参考文献

一、理论基础

果蝇优化算法(Fruit Fly Optimization Algorithm, FOA)是基于果蝇觅食行为的仿生学原理而提出的一种新兴群体智能优化算法，最早由台湾华夏科技大学的潘文超教授于2011年提出来的。
果蝇优化算法(FOA)通过模拟果蝇利用敏锐的嗅觉和视觉进行捕食的过程，FOA实现对解空间的群体迭代搜索。FOA原理易懂、操作简单、易于实现，具有较强的局部搜索能力。

二、算法步骤

1、启发

果蝇本身在感觉和感知方面优于其他物种，尤其是在嗅觉和视觉方面，如图1所示。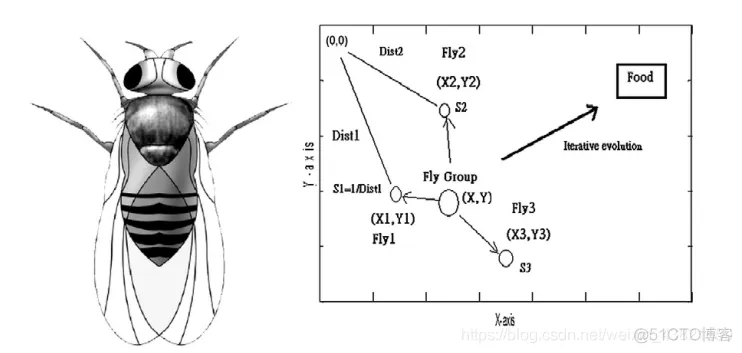

图1 果蝇的身体外观和群体迭代觅食

果蝇的嗅觉器官能发现空气中漂浮的各种气味；它甚至能闻到40公里外的食物。然后，当它接近食物位置，也可以用它灵敏的视觉找到食物和同伴聚集的位置，并朝那个方向飞行。

2、方向和距离

随机初始果蝇群体位置。

3、气味浓度判断值

由于无法知道食物的位置，因此首先估计到源头的距离(dist)，然后计算气味浓度判断值(s)，该值是距离的倒数。

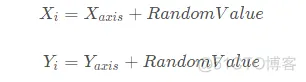
4、适应度评估

将气味浓度判断值代入气味浓度判断函数(或称为适应度函数)，找出果蝇个体位置的气味浓度。

5、寻找最优个体

找出果蝇群中气味浓度最大的果蝇(寻找最优个体)。

6、飞行

保持最佳的气味浓度值和x , y x,yx,y坐标，此时果蝇群将利用视觉飞向该位置。

7、迭代优化

进入迭代优化，重复执行步骤2~5然后判断气味浓度是否优于之前的迭代气味浓度，如果是，则执行步骤6。

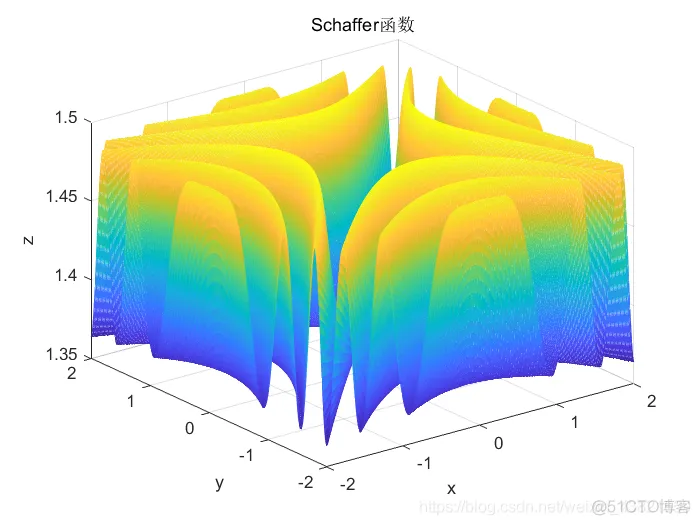
三、案例背景

问题描述

四、MATLAB程序实现

1、清空环境变量

程序运行之前，清除工作空间Workspace中的变量及Command Window中的命令。具体程序如下：

登录后复制

%% 清空环境变量
clc;
clear;

• 1.
• 2.
• 3.

2、初始化参数

在计算之前，需要对参数进行初始化。同时，为了加快程序的执行速度，对于程序中涉及的一些过程变量，需要预分配其存储容量。具体程序如下：

登录后复制

%% 随机初始化果蝇群体位置
X_axis = 10*rand(1, 2);
Y_axis = 10*rand(1, 2);
%% 设置参数
maxgen = 200;           % 迭代次数
sizepop = 20;           % 种群规模

• 1.
• 2.
• 3.
• 4.
• 5.
• 6.

• 1
• 2
• 3
• 4
• 5
• 6

3、寻找初始最优

登录后复制

%% 个体和速度最大和最小值
for i = 1:sizepop
    % 随机方向与距离
    X(i, :) = X_axis + 2*rand(1, 2)-1;
    Y(i, :) = Y_axis + 2*rand(1, 2)-1;
    % 距离和气味浓度
    D(i, :) = sqrt(X(i, :).^2+Y(i, :).^2);
    S(i, :) = 1./D(i, :);
    % 适应度函数Schaffer
    Smell(i) = 0.5+(cos(sin(abs(S(i, 1)^2-S(i, 2)^2))^2-0.5)/(1+0.001*(S(i, 1)^2+S(i, 2)^2))^2);
end
% 找出此果蝇群体中味道浓度最低的果蝇(求极小值)
[bestSmell bestindex]=min(Smell);
% 最佳气味浓度、果蝇位置、适应度最优位置
X_axis = X(bestindex, :);
Y_axis = Y(bestindex, :);
Smellbest = bestSmell;
FXbest = S(bestindex, 1);
FYbest = S(bestindex, 2);

• 1.
• 2.
• 3.
• 4.
• 5.
• 6.
• 7.
• 8.
• 9.
• 10.
• 11.
• 12.
• 13.
• 14.
• 15.
• 16.
• 17.
• 18.
• 19.

4、迭代寻优

迭代寻优为整个算法的核心。代码如下：

登录后复制

%% 果蝇迭代寻优
for gen = 1:maxgen
    % 粒子位置和速度更新
    for i = 1:sizepop
        X(i, :) = X_axis + 2*rand(1, 2)-1;
        Y(i, :) = Y_axis + 2*rand(1, 2)-1;
        D(i, :) = sqrt(X(i, :).^2+Y(i, :).^2);
        S(i, :) = 1./D(i, :);
        % 适应度函数Schaffer
        Smell(i) = 0.5+(cos(sin(abs(S(i, 1)^2-S(i, 2)^2))^2-0.5)/(1+0.001*(S(i, 1)^2+S(i, 2)^2))^2);
    end
    % 根据气味浓度值寻找极值
    [bestSmell bestindex]=min(Smell);
    % 保留最佳值位置
    if bestSmell < Smellbest
        X_axis = X(bestindex, :);
        Y_axis = Y(bestindex, :);
        Smellbest = bestSmell;
        FXbest = S(bestindex, 1);
        FYbest = S(bestindex, 2);
    end
    % 每代最优Smell值记录到yy数组中，并记录最优迭代坐标
    yy(gen) = Smellbest;
    Xbest(gen, :) = X_axis;
    Ybest(gen, :) = Y_axis;
end

• 1.
• 2.
• 3.
• 4.
• 5.
• 6.
• 7.
• 8.
• 9.
• 10.
• 11.
• 12.
• 13.
• 14.
• 15.
• 16.
• 17.
• 18.
• 19.
• 20.
• 21.
• 22.
• 23.
• 24.
• 25.
• 26.

5、结果显示

为了更为直观地对结果进行观察和分析，将寻找到的最优自变量及其最优函数值显示在Command Window中。具体程序如下：

登录后复制

%% 结果显示
disp(['适应度函数最优位置：', num2str(FXbest), ',', num2str(FYbest)]);
disp(['适应度函数最优解：', num2str(yy(end))]);

• 1.
• 2.
• 3.

由于各个果蝇的初始位置是随机生成的，因此每次运行的结果都会有所不同。某次运行的结果如下：

登录后复制

适应度函数最优位置：0.50068,42.8868
适应度函数最优解：0.61574

• 1.
• 2.

6、绘图

为了更为直观地对结果进行观察和分析，以图形的形式将结果显示出来，具体程序如下：

登录后复制

%% 绘制迭代味道浓度与果蝇飞行路径趋势图
figure(1);
plot(yy, 'r', 'linewidth', 2);
title('优化过程', 'fontsize', 12)
xlabel('迭代次数', 'fontsize', 12); ylabel('气味浓度(适应度值)', 'fontsize', 12);
figure(2);
gen = 1:maxgen;
plot(Xbest(:, 1), Ybest(:, 1), 'r.');             % 绘制果蝇群X_axis，Y_axis的变化
hold on;
plot(Xbest(:, 2), Ybest(:, 2), 'b.');
title('果蝇优化算法寻优路线', 'fontsize',14)
xlabel('X-axis', 'fontsize', 12); ylabel('Y-axis', 'fontsize', 12);

• 1.
• 2.
• 3.
• 4.
• 5.
• 6.
• 7.
• 8.
• 9.
• 10.
• 11.
• 12.

果蝇优化算法优化过程如图3所示。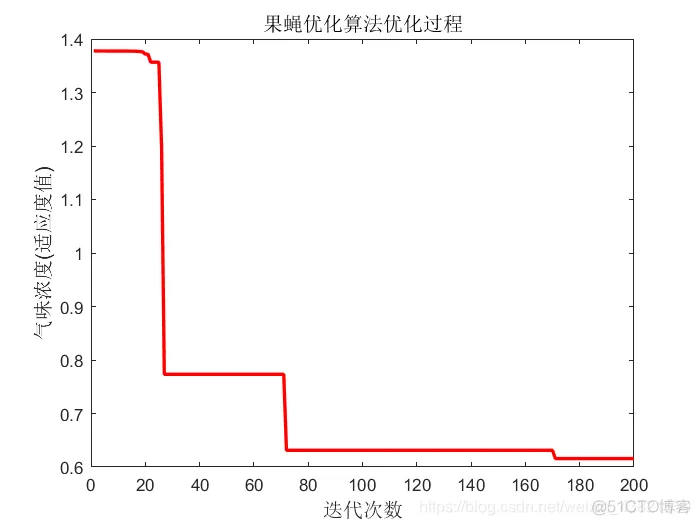

图3 果蝇优化算法优化过程

果蝇优化算法寻优路线如图4所示。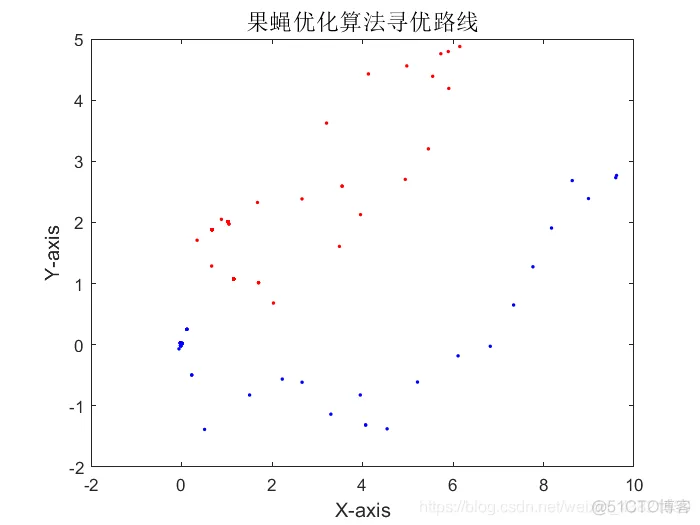

图4 果蝇优化算法寻优路线

五、参考文献

[1] Pan W T . A new Fruit Fly Optimization Algorithm: Taking the financial distress model as an example[J]. Knowledge-Based Systems, 2012, 26(2):69-74.完整代码或者仿真咨询添加QQ1575304183
[2] 松间沙路hba646333407. 果蝇优化算法(Fruit Fly Optimization Algorithm，FOA)-Matlab源码. 优快云博客.