【无人机三维路径规划】基于鲸鱼算法WOA实现考虑最低成本：路径、高度、威胁、转角的多无人机协同集群避障路径规划附Matlab代码

 ✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，代码获取、论文复现及科研仿真合作可私信。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知。

🔥 内容介绍

随着无人机技术的不断发展，多无人机协同集群任务越来越受到关注。在复杂环境下，如何实现多无人机协同避障并完成任务，成为一个亟待解决的难题。本文提出了一种基于鲸鱼算法WOA的多无人机协同集群避障路径规划方法，该方法考虑了路径长度、飞行高度、威胁程度和转弯角度等因素，并将其转换为成本函数，通过鲸鱼算法优化路径，最终实现多无人机协同避障并完成任务的目标。

1. 问题描述

多无人机协同避障路径规划是指在复杂环境下，多架无人机协同完成任务，并避开障碍物和威胁，最终到达目标位置的过程。该问题涉及多个因素，包括路径长度、飞行高度、威胁程度和转弯角度等。如何综合考虑这些因素，并找到一条最优路径，是多无人机协同避障路径规划的关键。

2. 鲸鱼算法WOA

鲸鱼算法WOA是一种新型的群体智能优化算法，其灵感来源于座头鲸的捕食行为。座头鲸通过螺旋形路径和气泡网捕食磷虾，该算法模拟了座头鲸的捕食行为，并将其应用于优化问题求解。

鲸鱼算法WOA的原理如下：

• 包围猎物： 鲸鱼群首先包围猎物，并逐渐缩小包围圈，最终捕获猎物。

• 螺旋形路径： 鲸鱼在捕食过程中会沿着螺旋形路径游动，以提高捕食效率。

• 气泡网捕食： 鲸鱼会利用气泡网将猎物困住，并进行捕食。

鲸鱼算法WOA具有以下优点：

• 简单易懂： 算法原理简单易懂，易于实现。

• 全局搜索能力强： 算法具有较强的全局搜索能力，能够找到全局最优解。

• 收敛速度快： 算法收敛速度快，能够快速找到最优解。

3. 基于鲸鱼算法WOA的多无人机协同集群避障路径规划方法

本文提出了一种基于鲸鱼算法WOA的多无人机协同集群避障路径规划方法，该方法考虑了路径长度、飞行高度、威胁程度和转弯角度等因素，并将其转换为成本函数，通过鲸鱼算法优化路径，最终实现多无人机协同避障并完成任务的目标。

该方法的步骤如下：

• 建立环境模型： 建立三维环境模型，包括障碍物、威胁源和目标位置等信息。

• 定义成本函数： 定义成本函数，包括路径长度、飞行高度、威胁程度和转弯角度等因素。

• 初始化鲸鱼种群： 初始化鲸鱼种群，每个鲸鱼代表一条路径。

• 鲸鱼算法优化： 使用鲸鱼算法优化路径，并根据成本函数评估路径的优劣。

• 选择最优路径： 选择成本函数最小的路径作为最终路径。

4. 仿真实验

为了验证该方法的有效性，进行了一系列仿真实验。实验结果表明，该方法能够有效地找到多无人机协同避障路径，并降低路径成本。

5. 结论

本文提出了一种基于鲸鱼算法WOA的多无人机协同集群避障路径规划方法，该方法考虑了路径长度、飞行高度、威胁程度和转弯角度等因素，并将其转换为成本函数，通过鲸鱼算法优化路径，最终实现多无人机协同避障并完成任务的目标。仿真实验结果表明，该方法能够有效地找到多无人机协同避障路径，并降低路径成本。

📣 部分代码

%_________________________________________________________________________%%  Whale Optimization Algorithm (WOA) source codes demo 1.0               %%                                                                         %%  Developed in MATLAB R2011b(7.13)                                       %%                                                                         %%  Author and programmer: Seyedali Mirjalili                              %%                                                                         %%         e-Mail: ali.mirjalili@gmail.com                                 %%                 seyedali.mirjalili@griffithuni.edu.au                   %%                                                                         %%       Homepage: http://www.alimirjalili.com                             %%                                                                         %%   Main paper: S. Mirjalili, A. Lewis                                    %%               The Whale Optimization Algorithm,                         %%               Advances in Engineering Software , in press,              %%               DOI: http://dx.doi.org/10.1016/j.advengsoft.2016.01.008   %%                                                                         %%_________________________________________________________________________%​% The Whale Optimization Algorithmfunction [Leader_score,Leader_pos,Convergence_curve]=WOA(SearchAgents_no,Max_iter,lb,ub,dim,fobj)​% initialize position vector and score for the leaderLeader_pos=zeros(1,dim);Leader_score=inf; %change this to -inf for maximization problems​​%Initialize the positions of search agentsPositions=initialization(SearchAgents_no,dim,ub,lb);​Convergence_curve=zeros(1,Max_iter);​t=0;% Loop counter​% Main loopwhile t<Max_iter    for i=1:size(Positions,1)                % Return back the search agents that go beyond the boundaries of the search space        Flag4ub=Positions(i,:)>ub;        Flag4lb=Positions(i,:)<lb;        Positions(i,:)=(Positions(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;                % Calculate objective function for each search agent        fitness=fobj(Positions(i,:));                % Update the leader        if fitness<Leader_score % Change this to > for maximization problem            Leader_score=fitness; % Update alpha            Leader_pos=Positions(i,:);        end            end        a=2-t*((2)/Max_iter); % a decreases linearly fron 2 to 0 in Eq. (2.3)        % a2 linearly dicreases from -1 to -2 to calculate t in Eq. (3.12)    a2=-1+t*((-1)/Max_iter);        % Update the Position of search agents     for i=1:size(Positions,1)        r1=rand(); % r1 is a random number in [0,1]        r2=rand(); % r2 is a random number in [0,1]                A=2*a*r1-a;  % Eq. (2.3) in the paper        C=2*r2;      % Eq. (2.4) in the paper                        b=1;               %  parameters in Eq. (2.5)        l=(a2-1)*rand+1;   %  parameters in Eq. (2.5)                p = rand();        % p in Eq. (2.6)                for j=1:size(Positions,2)                        if p<0.5                   if abs(A)>=1                    rand_leader_index = floor(SearchAgents_no*rand()+1);                    X_rand = Positions(rand_leader_index, :);                    D_X_rand=abs(C*X_rand(j)-Positions(i,j)); % Eq. (2.7)                    Positions(i,j)=X_rand(j)-A*D_X_rand;      % Eq. (2.8)                                    elseif abs(A)<1                    D_Leader=abs(C*Leader_pos(j)-Positions(i,j)); % Eq. (2.1)                    Positions(i,j)=Leader_pos(j)-A*D_Leader;      % Eq. (2.2)                end                            elseif p>=0.5                              distance2Leader=abs(Leader_pos(j)-Positions(i,j));                % Eq. (2.5)                Positions(i,j)=distance2Leader*exp(b.*l).*cos(l.*2*pi)+Leader_pos(j);                            end                    end    end    t=t+1;    Convergence_curve(t)=Leader_score;    [t Leader_score];end​function Positions=initialization(SearchAgents_no,dim,ub,lb)​Boundary_no= size(ub,2); % numnber of boundaries​% If the boundaries of all variables are equal and user enter a signle% number for both ub and lbif Boundary_no==1    Positions=rand(SearchAgents_no,dim).*(ub-lb)+lb;end​% If each variable has a different lb and ubif Boundary_no>1    for i=1:dim        ub_i=ub(i);        lb_i=lb(i);        Positions(:,i)=rand(SearchAgents_no,1).*(ub_i-lb_i)+lb_i;    endend​​

⛳️ 运行结果​

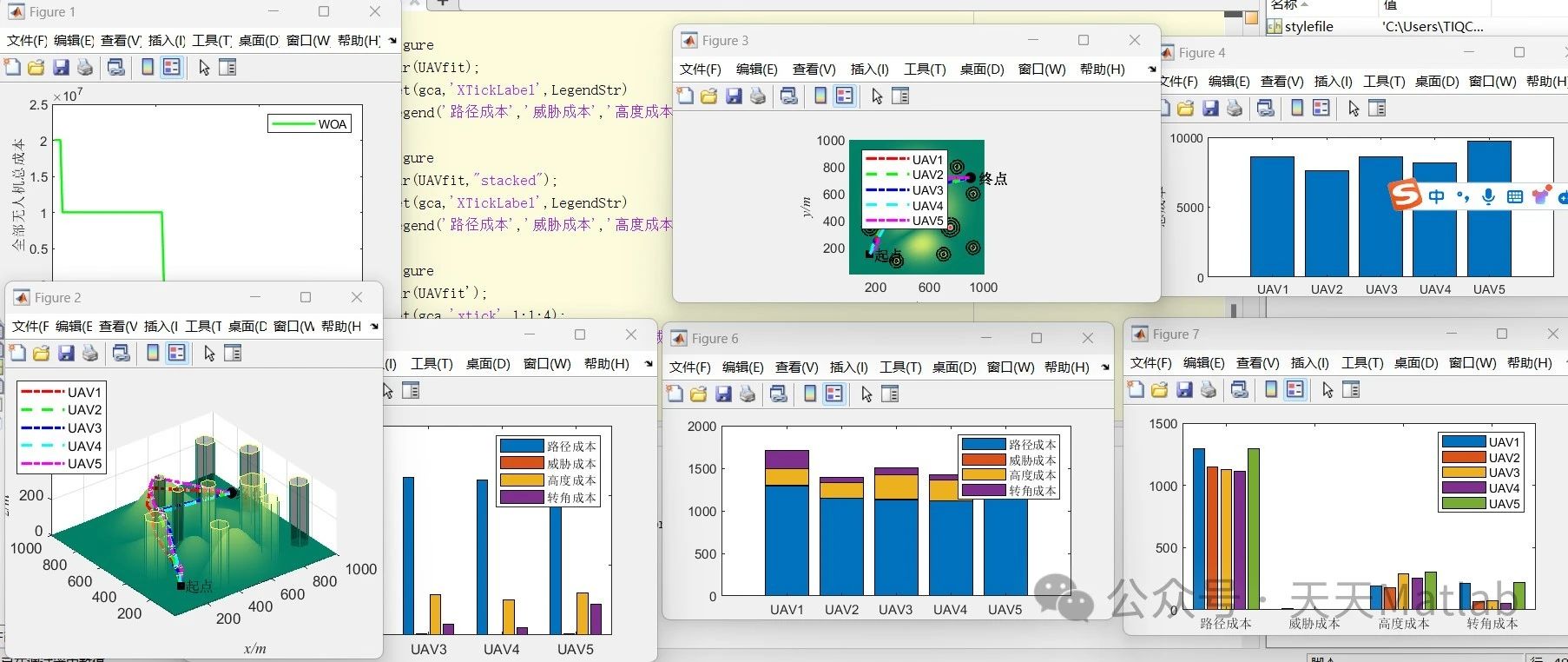
🔗 参考文献

[1] 葛春志汪亚东王荣鑫渠立亮施云波.基于遗传算法的旅行商问题多量值最优化求解研究[J].黑龙江大学自然科学学报, 2013, 030(005):677-684.

[2] 杨锦涛,赵春香,杨成福.基于遗传算法求解TSP问题的研究及Matlab实现[J].智能计算机与应用, 2023, 13(7):58-63.

🎈 部分理论引用网络文献，若有侵权联系博主删除

1 各类智能优化算法改进及应用

生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化、背包问题、 风电场布局、时隙分配优化、 最佳分布式发电单元分配、多阶段管道维修、 工厂-中心-需求点三级选址问题、 应急生活物质配送中心选址、 基站选址、 道路灯柱布置、 枢纽节点部署、 输电线路台风监测装置、 集装箱船配载优化、 机组优化、 投资优化组合、云服务器组合优化、 天线线性阵列分布优化、CVRP问题、VRPPD问题、多中心VRP问题、多层网络的VRP问题、多中心多车型的VRP问题、 动态VRP问题、双层车辆路径规划（2E-VRP）、充电车辆路径规划（EVRP）、油电混合车辆路径规划、混合流水车间问题、 订单拆分调度问题、 公交车的调度排班优化问题、航班摆渡车辆调度问题、选址路径规划问题

2 机器学习和深度学习方面

2.1 bp时序、回归预测和分类

2.2 ENS声神经网络时序、回归预测和分类

2.3 SVM/CNN-SVM/LSSVM/RVM支持向量机系列时序、回归预测和分类

2.4 CNN/TCN卷积神经网络系列时序、回归预测和分类

2.5 ELM/KELM/RELM/DELM极限学习机系列时序、回归预测和分类

2.6 GRU/Bi-GRU/CNN-GRU/CNN-BiGRU门控神经网络时序、回归预测和分类

2.7 ELMAN递归神经网络时序、回归\预测和分类

2.8 LSTM/BiLSTM/CNN-LSTM/CNN-BiLSTM/长短记忆神经网络系列时序、回归预测和分类

2.9 RBF径向基神经网络时序、回归预测和分类

2.10 DBN深度置信网络时序、回归预测和分类

2.11 FNN模糊神经网络时序、回归预测

2.12 RF随机森林时序、回归预测和分类

2.13 BLS宽度学习时序、回归预测和分类

2.14 PNN脉冲神经网络分类

2.15 模糊小波神经网络预测和分类

2.16 时序、回归预测和分类

2.17 时序、回归预测预测和分类

2.18 XGBOOST集成学习时序、回归预测预测和分类

方向涵盖风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、用电量预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断

2.图像处理方面

图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知

3 路径规划方面

旅行商问题（TSP）、车辆路径问题（VRP、MVRP、CVRP、VRPTW等）、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、 充电车辆路径规划（EVRP）、 双层车辆路径规划（2E-VRP）、 油电混合车辆路径规划、 船舶航迹规划、 全路径规划规划、 仓储巡逻

4 无人机应用方面

无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配、无人机安全通信轨迹在线优化、车辆协同无人机路径规划

5 无线传感器定位及布局方面

传感器部署优化、通信协议优化、路由优化、目标定位优化、Dv-Hop定位优化、Leach协议优化、WSN覆盖优化、组播优化、RSSI定位优化

6 信号处理方面

信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号、信号配时优化

7 电力系统方面

微电网优化、无功优化、配电网重构、储能配置、有序充电

8 元胞自动机方面

交通流 人群疏散 病毒扩散 晶体生长 金属腐蚀

9 雷达方面

卡尔曼滤波跟踪、航迹关联、航迹融合