【DVHOP定位】一种基于RSSI的DV-HOP加权算法附matlab代码

 ✅作者简介：热爱科研的Matlab仿真开发者，修心和技术同步精进，代码获取、论文复现及科研仿真合作可私信。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知。

🔥 内容介绍

摘要

分布式无线传感器网络（WSN）是一种由大量传感器节点组成的新型网络，具有自组织、自愈合、低功耗等特点。WSN在环境监测、工业控制、医疗保健等领域有着广泛的应用。

DV-HOP定位算法是WSN中常用的定位算法之一。该算法基于每个传感器节点对相邻节点的距离估计，通过交换这些距离估计信息来计算每个节点的位置。DV-HOP算法的精度取决于距离估计的准确性。

传统的DV-HOP算法使用接收信号强度指示器（RSSI）来估计节点之间的距离。然而，RSSI受到许多因素的影响，如信号衰减、多径效应、障碍物阻挡等，因此其估计精度不高。

为了提高DV-HOP算法的精度，本文提出了一种基于RSSI的DV-HOP加权算法。该算法利用RSSI的统计特性，对RSSI进行加权处理，以提高距离估计的准确性。

算法原理

传统的DV-HOP算法使用以下公式来估计节点之间的距离：

d = k * RSSI^-α

其中，d为节点之间的距离，RSSI为接收信号强度指示器，k和α为常数。

然而，RSSI受到许多因素的影响，如信号衰减、多径效应、障碍物阻挡等，因此其估计精度不高。

为了提高DV-HOP算法的精度，本文提出了一种基于RSSI的DV-HOP加权算法。该算法利用RSSI的统计特性，对RSSI进行加权处理，以提高距离估计的准确性。

具体来说，该算法首先对RSSI进行预处理，以消除RSSI中的噪声和异常值。然后，该算法计算RSSI的均值和方差。最后，该算法使用以下公式对RSSI进行加权：

w = (RSSI - μ) / σ

其中，w为RSSI的权重，μ为RSSI的均值，σ为RSSI的方差。

加权后的RSSI可以用来估计节点之间的距离。该算法使用以下公式来估计节点之间的距离：

d = k * (w * RSSI)^-α

其中，d为节点之间的距离，w为RSSI的权重，RSSI为接收信号强度指示器，k和α为常数。

📣 部分代码

%~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~  DV-Hop算法  ~~~~~~~~~~~~~~~~~~~~~~~~%~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~% BorderLength-----正方形区域的边长，单位：m% NodeAmount-------网络节点的个数% BeaconAmount---信标节点数% Sxy--------------用于存储节点的序号，横坐标，纵坐标的矩阵%Beacon----------信标节点坐标矩阵;BeaconAmount*BeaconAmount%UN-------------未知节点坐标矩阵;2*UNAmount% Distance------未知节点到信标节点距离矩阵;2*BeaconAmount%h---------------节点间初始跳数矩阵%X---------------节点估计坐标初始矩阵,X=[x,y]'% R------------------节点的通信距离，一般为10-100m​clear,close all;BorderLength=100;NodeAmount=100;BeaconAmount=8;UNAmount=NodeAmount-BeaconAmount;R=50;% D=zeros(NodeAmount,NodeAmount);%未知节电到信标节点距离初始矩阵；BeaconAmount行NodeAmount列h=zeros(NodeAmount,NodeAmount);%初始跳数为0；BeaconAmount行NodeAmount列X=zeros(2,UNAmount);%节点估计坐标初始矩阵​%~~~~~~~~~~~~~~~~~~~~~~~~~~~~~在正方形区域内产生均匀分布的随机拓扑~~~~~~~~~~~~~~~~~~~~C=BorderLength.*rand(2,NodeAmount);%带逻辑号的节点坐标Sxy=[[1:NodeAmount];C];Beacon=[Sxy(2,1:BeaconAmount);Sxy(3,1:BeaconAmount)];%信标节点坐标UN=[Sxy(2,(BeaconAmount+1):NodeAmount);Sxy(3,(BeaconAmount+1):NodeAmount)];%未知节点坐标%画出节点分布图plot(Sxy(2,1:BeaconAmount),Sxy(3,1:BeaconAmount),'r*',Sxy(2,(BeaconAmount+1):NodeAmount),Sxy(3,(BeaconAmount+1):NodeAmount),'k.')xlim([0,BorderLength]);ylim([0,BorderLength]);title('* 红色信标节点 . 黑色未知节点')%~~~~~~~~~~~~~~~~~~~~~~~~~~~~初始化节点间距离、跳数矩阵~~~~~~~~~~~~~~~~~~~~~~for i=1:NodeAmount    for j=1:NodeAmount        Dall(i,j)=((Sxy(2,i)-Sxy(2,j))^2+(Sxy(3,i)-Sxy(3,j))^2)^0.5;%所有节点间相互距离        if (Dall(i,j)<=R)&(Dall(i,j)>0)            h(i,j)=1;%初始跳数矩阵        elseif i==j            h(i,j)=0;        else h(i,j)=inf;        end    endend%~~~~~~~~~~~~~~~~~~~~~~~~~最短路经算法计算节点间跳数~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~for k=1:NodeAmount    for i=1:NodeAmount        for j=1:NodeAmount            if h(i,k)+h(k,j)<h(i,j)%min(h(i,j),h(i,k)+h(k,j))                h(i,j)=h(i,k)+h(k,j);            end        end    endendh%~~~~~~~~~~~~~~~~~~~~~~~~~求每个信标节点的校正值~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~h1=h(1:BeaconAmount,1:BeaconAmount); D1=Dall(1:BeaconAmount,1:BeaconAmount);for i=1:BeaconAmount    dhop(i,1)=sum(D1(i,:))/sum(h1(i,:));%每个信标节点的平均每跳距离endD2=Dall(1:BeaconAmount,(BeaconAmount+1):NodeAmount);%BeaconAmount行UNAmount列for i=1:BeaconAmount    for j=1:UNAmount        if min(D2(:,j))==D2(i,j)            Dhop(1,j)=D2(i,j);%未知节点从最近的信标获得校正值        end    endendDhop%~~~~~~~~~~~~~~~~~~~~~~~~~~~用跳数估计距离~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~hop1=h(1:BeaconAmount,(BeaconAmount+1):NodeAmount)%未知节点到信标跳数，BeaconAmount行UNAmount列for i=1:UNAmount    hop=Dhop(1,i);%hop为从最近信标获得的校正值    Distance(:,i)=hop*hop1(:,i);%%Beacon行UN列；end% %~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~最小二乘法求未知点坐标~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~d=Distance;for i=1:2    for j=1:(BeaconAmount-1)      a(i,j)=Beacon(i,j)-Beacon(i,BeaconAmount);    endendA=-2*(a');% d=d1'; for m=1:UNAmount      for i=1:(BeaconAmount-1)         B(i,1)=d(i,m)^2-d(BeaconAmount,m)^2-Beacon(1,i)^2+Beacon(1,BeaconAmount)^2-Beacon(2,i)^2+Beacon(2,BeaconAmount)^2;     end           X1=inv(A'*A)*A'*B;           X(1,m)=X1(1,1);           X(2,m)=X1(2,1); end UN X for i=1:UNAmount     error(1,i)=(((X(1,i)-UN(1,i))^2+(X(2,i)-UN(2,i))^2)^0.5); end figure;plot(error,'-o') title('每个未知节点的误差') error=sum(error)/UNAmount Accuracy=error/R

⛳️ 运行结果

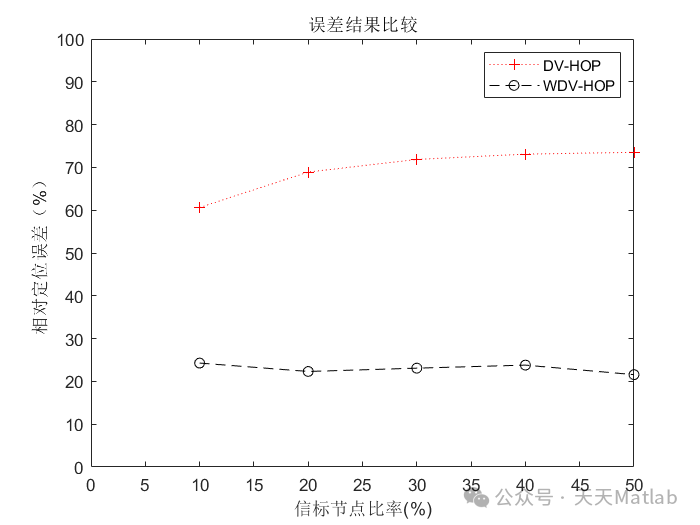
仿真结果

为了评估该算法的性能，我们在MATLAB中进行了仿真。仿真结果表明，该算法的精度明显高于传统的DV-HOP算法。

本文提出了一种基于RSSI的DV-HOP加权算法。该算法利用RSSI的统计特性，对RSSI进行加权处理，以提高距离估计的准确性。仿真结果表明，该算法的精度明显高于传统的DV-HOP算法。

🔗 参考文献

[1]蔡燕,陈华.基于RSSI比例系数跳数加权的DV-Hop定位算法[J].科技风, 2017, 000(010):59-59.DOI:10.19392/j.cnki.1671-7341.201710051.

🎈 部分理论引用网络文献，若有侵权联系博主删除

🎁  关注我领取海量matlab电子书和数学建模资料

👇  私信完整代码和数据获取及论文数模仿真定制

1 各类智能优化算法改进及应用

生产调度、经济调度、装配线调度、充电优化、车间调度、发车优化、水库调度、三维装箱、物流选址、货位优化、公交排班优化、充电桩布局优化、车间布局优化、集装箱船配载优化、水泵组合优化、解医疗资源分配优化、设施布局优化、可视域基站和无人机选址优化、背包问题、 风电场布局、时隙分配优化、 最佳分布式发电单元分配、多阶段管道维修、 工厂-中心-需求点三级选址问题、 应急生活物质配送中心选址、 基站选址、 道路灯柱布置、 枢纽节点部署、 输电线路台风监测装置、 集装箱船配载优化、 机组优化、 投资优化组合、云服务器组合优化、 天线线性阵列分布优化

2 机器学习和深度学习方面

2.1 bp时序、回归预测和分类

2.2 ENS声神经网络时序、回归预测和分类

2.3 SVM/CNN-SVM/LSSVM/RVM支持向量机系列时序、回归预测和分类

2.4 CNN/TCN卷积神经网络系列时序、回归预测和分类

2.5 ELM/KELM/RELM/DELM极限学习机系列时序、回归预测和分类

2.6 GRU/Bi-GRU/CNN-GRU/CNN-BiGRU门控神经网络时序、回归预测和分类

2.7 ELMAN递归神经网络时序、回归\预测和分类

2.8 LSTM/BiLSTM/CNN-LSTM/CNN-BiLSTM/长短记忆神经网络系列时序、回归预测和分类

2.9 RBF径向基神经网络时序、回归预测和分类

2.10 DBN深度置信网络时序、回归预测和分类

2.11 FNN模糊神经网络时序、回归预测

2.12 RF随机森林时序、回归预测和分类

2.13 BLS宽度学习时序、回归预测和分类

2.14 PNN脉冲神经网络分类

2.15 模糊小波神经网络预测和分类

2.16 时序、回归预测和分类

2.17 时序、回归预测预测和分类

2.18 XGBOOST集成学习时序、回归预测预测和分类

方向涵盖风电预测、光伏预测、电池寿命预测、辐射源识别、交通流预测、负荷预测、股价预测、PM2.5浓度预测、电池健康状态预测、用电量预测、水体光学参数反演、NLOS信号识别、地铁停车精准预测、变压器故障诊断

2.图像处理方面

图像识别、图像分割、图像检测、图像隐藏、图像配准、图像拼接、图像融合、图像增强、图像压缩感知

3 路径规划方面

旅行商问题（TSP）、车辆路径问题（VRP、MVRP、CVRP、VRPTW等）、无人机三维路径规划、无人机协同、无人机编队、机器人路径规划、栅格地图路径规划、多式联运运输问题、 充电车辆路径规划（EVRP）、 双层车辆路径规划（2E-VRP）、 油电混合车辆路径规划、 船舶航迹规划、 全路径规划规划、 仓储巡逻

4 无人机应用方面

无人机路径规划、无人机控制、无人机编队、无人机协同、无人机任务分配、无人机安全通信轨迹在线优化、车辆协同无人机路径规划

5 无线传感器定位及布局方面

传感器部署优化、通信协议优化、路由优化、目标定位优化、Dv-Hop定位优化、Leach协议优化、WSN覆盖优化、组播优化、RSSI定位优化

6 信号处理方面

信号识别、信号加密、信号去噪、信号增强、雷达信号处理、信号水印嵌入提取、肌电信号、脑电信号、信号配时优化

7 电力系统方面

微电网优化、无功优化、配电网重构、储能配置、有序充电

8 元胞自动机方面

交通流 人群疏散 病毒扩散 晶体生长 金属腐蚀

9 雷达方面

卡尔曼滤波跟踪、航迹关联、航迹融合