✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,matlab项目合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
更多Matlab仿真内容点击👇
⛄ 内容介绍
The sparrow search algorithm (ssA) is a relatively new swarm intelligence heuristic algorithm. It has fast convergence speed, strong optimization ability and more extensive application scenarios compared with traditional heuristic search methods. And thus, the ssA is attracting the attention of researchers in different fields. However, there are deficiencies of initial population quality, search ability, and population diversity in the ssA. Therefore, this paper proposes an improved sparrow search algorithm (IssA). The IssA uses skew tent map-based chaotic method to produce initial population for a higher quality of convergence. For the location update of the producer sparrows during the iterations, the IssA introduces a non-linear decreasing weight, promoting both exploration and exploitation of the search space, to improve the convergence and search precision. And the mutation strategy is employed to update the location of the scrounger sparrows with lower energy and the chaotic search is combined with the local exploitation for the scroungers with higher energy, which can enhance the diversity and avoid trapping in local optimum. simulation experiments are carriedout on 26 benchmark test functions. And the results show that the IssA is superior to or at least competitive to the ssA in the convergence properties of accuracy, speed, and stability.


⛄ 部分代码
function [fMin , bestX,Convergence_curve ] = SSA(pop, M,c,d,dim,fobj )
P_percent = 0.2; % The population size of producers accounts for "P_percent" percent of the total population size
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
pNum = round( pop * P_percent ); % The population size of the producers
lb= c.*ones( 1,dim ); % Lower limit/bounds/ a vector
ub= d.*ones( 1,dim ); % Upper limit/bounds/ a vector
%Initialization
for i = 1 : pop
x( i, : ) = lb + (ub - lb) .* rand( 1, dim );
fit( i ) = fobj( x( i, : ) ) ;
end
pFit = fit;
pX = x; % The individual's best position corresponding to the pFit
[ fMin, bestI ] = min( fit ); % fMin denotes the global optimum fitness value
bestX = x( bestI, : ); % bestX denotes the global optimum position corresponding to fMin
% Start updating the solutions.
for t = 1 : M
[ ans, sortIndex ] = sort( pFit );% Sort.
[fmax,B]=max( pFit );
worse= x(B,:);
r2=rand(1);
if(r2<0.8)
for i = 1 : pNum % Equation (3)
r1=rand(1);
x( sortIndex( i ), : ) = pX( sortIndex( i ), : )*exp(-(i)/(r1*M));
x( sortIndex( i ), : ) = Bounds( x( sortIndex( i ), : ), lb, ub );
fit( sortIndex( i ) ) = fobj( x( sortIndex( i ), : ) );
end
else
for i = 1 : pNum
x( sortIndex( i ), : ) = pX( sortIndex( i ), : )+randn(1)*ones(1,dim);
x( sortIndex( i ), : ) = Bounds( x( sortIndex( i ), : ), lb, ub );
fit( sortIndex( i ) ) = fobj( x( sortIndex( i ), : ) );
end
end
[ fMMin, bestII ] = min( fit );
bestXX = x( bestII, : );
for i = ( pNum + 1 ) : pop % Equation (4)
A=floor(rand(1,dim)*2)*2-1;
if( i>(pop/2))
x( sortIndex(i ), : )=randn(1)*exp((worse-pX( sortIndex( i ), : ))/(i)^2);
else
x( sortIndex( i ), : )=bestXX+(abs(( pX( sortIndex( i ), : )-bestXX)))*(A'*(A*A')^(-1))*ones(1,dim);
end
x( sortIndex( i ), : ) = Bounds( x( sortIndex( i ), : ), lb, ub );
fit( sortIndex( i ) ) = fobj( x( sortIndex( i ), : ) );
end
c=randperm(numel(sortIndex));
b=sortIndex(c(1:20));
for j = 1 : length(b) % Equation (5)
if( pFit( sortIndex( b(j) ) )>(fMin) )
x( sortIndex( b(j) ), : )=bestX+(randn(1,dim)).*(abs(( pX( sortIndex( b(j) ), : ) -bestX)));
else
x( sortIndex( b(j) ), : ) =pX( sortIndex( b(j) ), : )+(2*rand(1)-1)*(abs(pX( sortIndex( b(j) ), : )-worse))/ ( pFit( sortIndex( b(j) ) )-fmax+1e-50);
end
x( sortIndex(b(j) ), : ) = Bounds( x( sortIndex(b(j) ), : ), lb, ub );
fit( sortIndex( b(j) ) ) = fobj( x( sortIndex( b(j) ), : ) );
end
for i = 1 : pop
if ( fit( i ) < pFit( i ) )
pFit( i ) = fit( i );
pX( i, : ) = x( i, : );
end
if( pFit( i ) < fMin )
fMin= pFit( i );
bestX = pX( i, : );
end
end
Convergence_curve(t)=fMin;
end
% Application of simple limits/bounds
function s = Bounds( s, Lb, Ub)
% Apply the lower bound vector
temp = s;
I = temp < Lb;
temp(I) = Lb(I);
% Apply the upper bound vector
J = temp > Ub;
temp(J) = Ub(J);
% Update this new move
s = temp;
%---------------------------------------------------------------------------------------------------------------------------
⛄ 运行结果
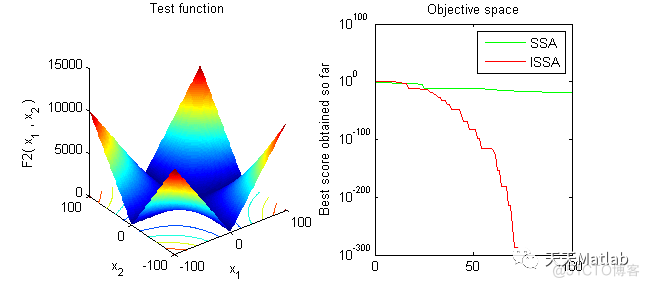
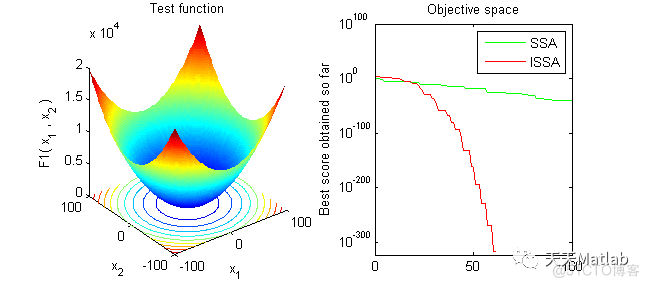
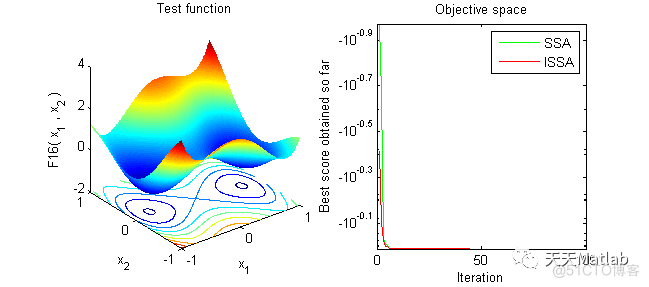




 文章提出了一种改进的麻雀搜索算法(IssA),利用偏斜帐篷映射的混沌方法生成高质量初始种群,通过非线性递减权重增强搜索空间的探索与开发,同时结合遗传变异策略和局部利用,提高低能量麻雀的位置更新和高能量麻雀的多样性,避免陷入局部最优。通过对26个基准测试函数的模拟实验,证明了IssA在精度、速度和稳定性方面优于或至少与原ssA竞争。
文章提出了一种改进的麻雀搜索算法(IssA),利用偏斜帐篷映射的混沌方法生成高质量初始种群,通过非线性递减权重增强搜索空间的探索与开发,同时结合遗传变异策略和局部利用,提高低能量麻雀的位置更新和高能量麻雀的多样性,避免陷入局部最优。通过对26个基准测试函数的模拟实验,证明了IssA在精度、速度和稳定性方面优于或至少与原ssA竞争。
















 12万+
12万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








