【状态估计】使用卡尔曼滤波技术对传感器真实位置和加速度数据进行状态估计（Matlab实现）

原创已于 2025-04-07 19:00:18 修改 · 1.2k 阅读

8 ·

CC 4.0 BY-SA版权

文章标签：

#matlab #javascript #开发语言

于 2025-04-02 18:17:51 首次发布

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

💥1 概述

一、引言

在众多工程与科技领域，如自动驾驶、机器人导航、航空航天以及工业自动化控制等，精确获取传感器的位置和运动状态信息至关重要。然而，传感器测量值往往受到各种噪声干扰，包括系统内部噪声、环境噪声等，使得原始数据存在较大误差，无法直接反映真实状态。卡尔曼滤波技术作为一种强大的最优估计理论算法，能够有效融合传感器的测量数据与系统的先验知识，对传感器的真实位置和加速度等状态进行精准估计，为复杂系统的稳定运行、精确控制提供坚实的数据基础。

二、在传感器数据处理中的应用流程

1. 系统建模：针对传感器所在系统，建立符合其动态特性的状态空间模型。确定状态向量，通常包含位置、速度、加速度等信息构建状态转移矩阵，依据系统物理规律描述状态随时间的演变，如匀速运动模型、匀加速运动模型等不同假设下，状态转移矩阵形式各异；同时量化过程噪声协方差矩阵，考量系统不确定性因素。 2. 参数初始化：初始化状态估计值及其协方差矩阵。在系统启动初期，若无先验准确信息，可基于经验或粗略测量给定初始状态估计，协方差矩阵初始值通常设为较大值，表明对初始估计的不确定性较高，随着滤波迭代，逐步修正优化。 3. 数据融合与估计循环：传感器按固定采样周期采集数据，在每个采样时刻，首先依据当前状态估计和状态转移模型进行预测，得到预测状态与协方差；随后，将传感器测量的位置、加速度数据代入测量方程，结合预测结果，利用卡尔曼增益融合二者信息，更新得到当前时刻更精准的状态估计值与协方差，如此循环往复，持续提升状态估计精度。

三、优势

1.最优估计特性：卡尔曼滤波在均方误差最小意义下是最优的线性估计器。它能够在存在噪声干扰的情况下，巧妙平衡系统模型预测信息与传感器测量信息，使最终得到的状态估计值尽可能接近真实值，为系统决策提供可靠依据，例如在自动驾驶汽车轨迹规划中，精准的位置与速度估计保障行车安全与路线精准性。 2. 实时性与递推性：算法采用递推形式，仅需利用前一时刻的估计结果和当前时刻的测量值即可进行当前状态估计，无需存储大量历史数据，计算复杂度相对可控，能够满足实时性要求苛刻的应用场景，如工业机器人实时运动控制，在毫秒级时间内完成状态更新，确保操作精准流畅。 3. 对噪声适应性强：通过合理设置过程噪声与测量噪声协方差矩阵，卡尔曼滤波可灵活适应不同强度、特性的噪声环境。在复杂电磁干扰下的航空航天传感器数据处理，或是嘈杂工业现场的设备监测场景，它都能有效抑制噪声影响，提取可靠状态信息。

四、局限性与改进方向

1. 局限性：线性系统假设：卡尔曼滤波基于线性系统模型与线性测量方程，实际应用中，许多系统存在非线性特性，如卫星轨道动力学受复杂引力场影响、机器人关节运动存在摩擦等非线性因素，此时直接应用卡尔曼滤波会导致估计偏差增大，甚至失效。高斯噪声假设：算法假定过程噪声与测量噪声均服从高斯分布，现实情况并非总是如此，当噪声呈现非高斯特性，如存在脉冲噪声、厚尾分布噪声时，基于高斯假设的卡尔曼滤波性能会大打折扣，无法准确反映系统真实状态。 2. 改进方向：扩展卡尔曼滤波（EKF）：针对系统非线性问题，EKF 通过对非线性函数进行一阶泰勒展开线性化，近似应用卡尔曼滤波原理。在每次迭代中，重新计算线性化后的状态转移矩阵与测量矩阵，虽引入一定近似误差，但在一定程度上能处理弱非线性系统，广泛应用于车辆定位导航等领域。无迹卡尔曼滤波（UKF）：与 EKF 不同，UKF 基于无迹变换，选取一组确定性的样本点（Sigma 点）来近似状态分布，通过对这些样本点进行非线性变换传播，无需线性化操作，能更精准捕捉非线性系统特性，在强非线性、高精度要求场景如导弹制导、生物医学信号处理中有出色表现。粒子滤波（PF）：为应对非高斯噪声问题，PF 采用蒙特卡罗方法，用大量随机粒子来表示系统状态的概率分布，每个粒子携带状态信息，依据测量值对粒子权重进行更新、重采样，以逼近真实状态分布，适用于非线性、非高斯系统，如复杂环境下的目标跟踪，但计算成本较高，在实际应用中需平衡精度与计算资源。

五、结论

卡尔曼滤波技术凭借其卓越的状态估计能力，在处理传感器数据、还原真实位置与加速度状态方面发挥着不可替代的作用，为众多高科技领域的稳健发展筑牢根基。尽管存在一定局限性，但随着一系列改进算法的涌现与发展，它持续突破边界，不断适应更为复杂、严苛的应用环境，有望在未来科技创新浪潮中续写辉煌，助力人类探索更多未知领域。

📚2 运行结果

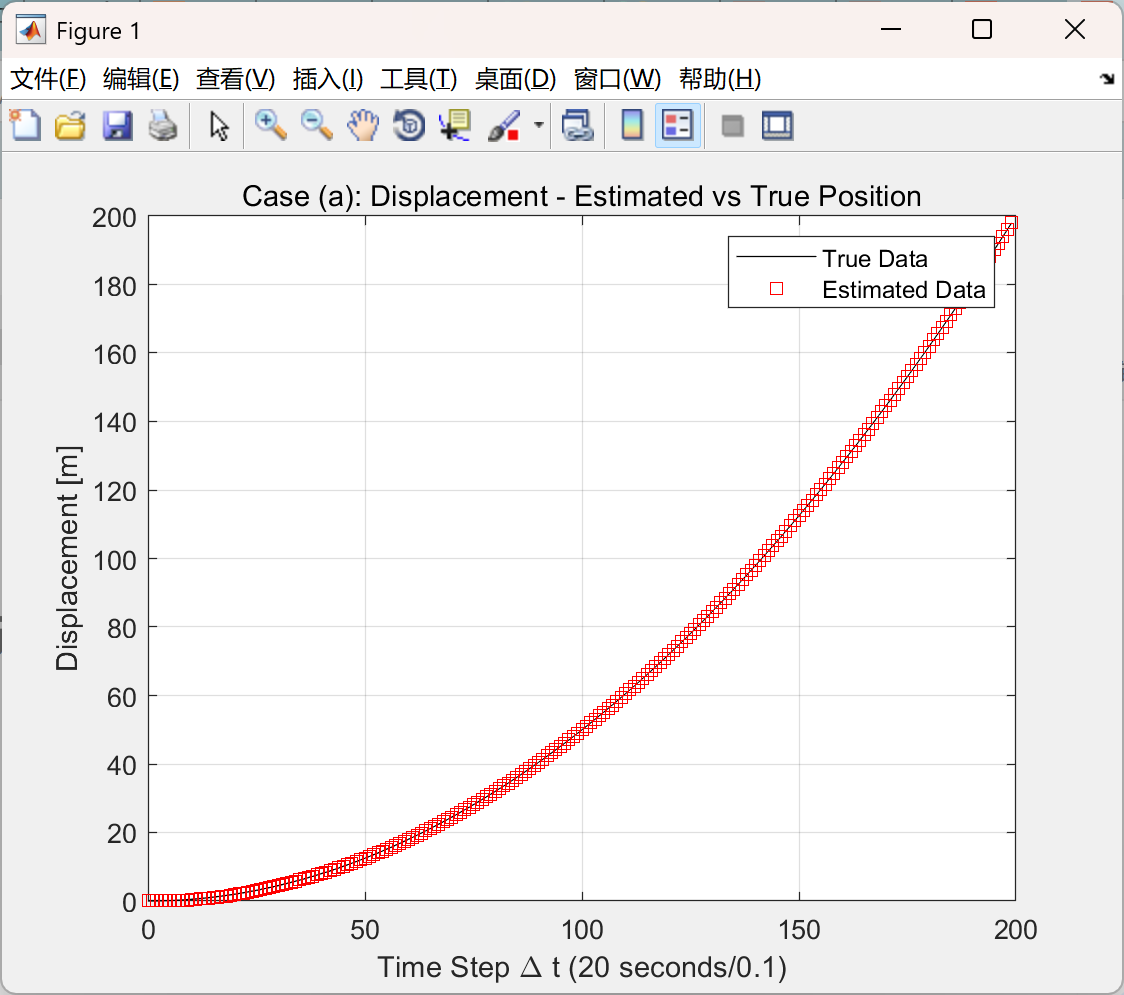
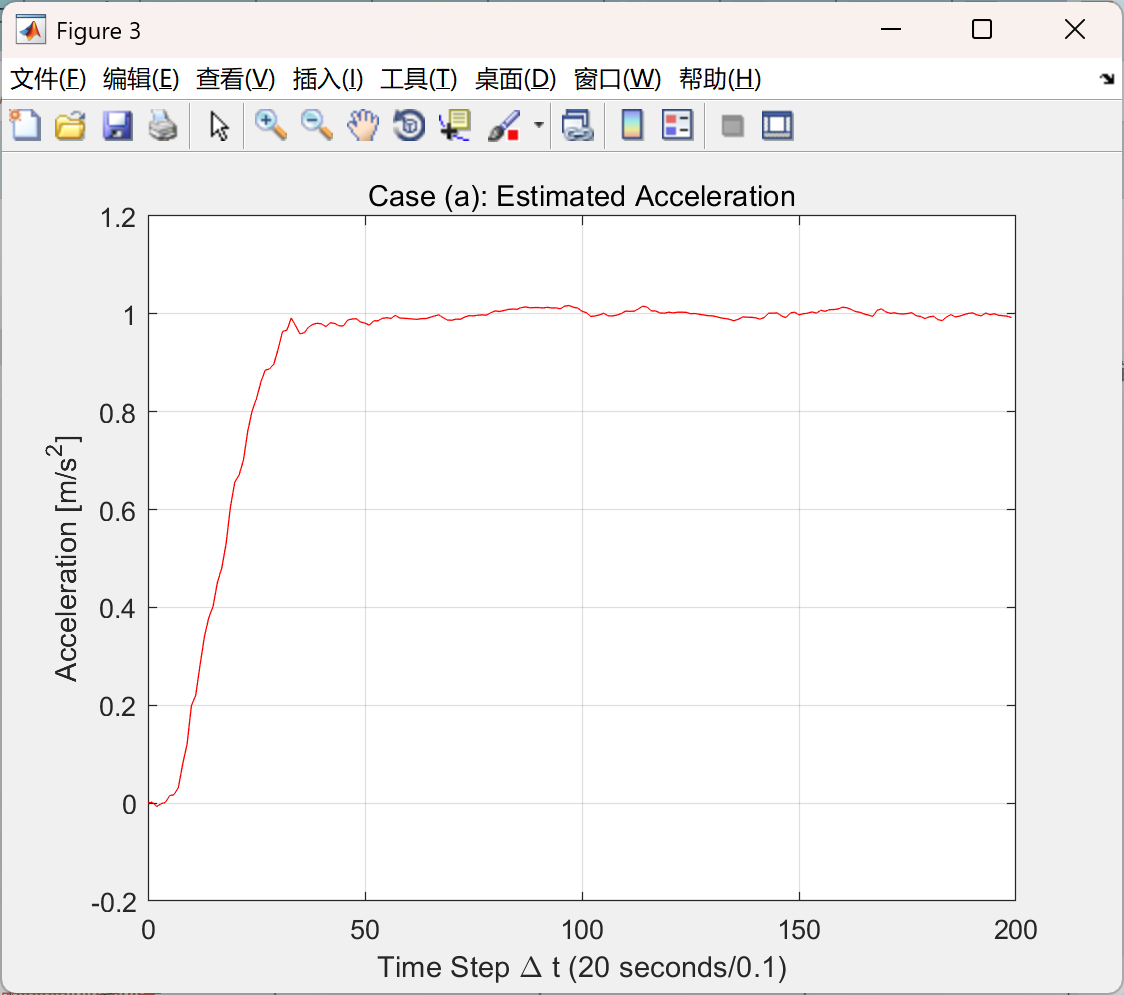
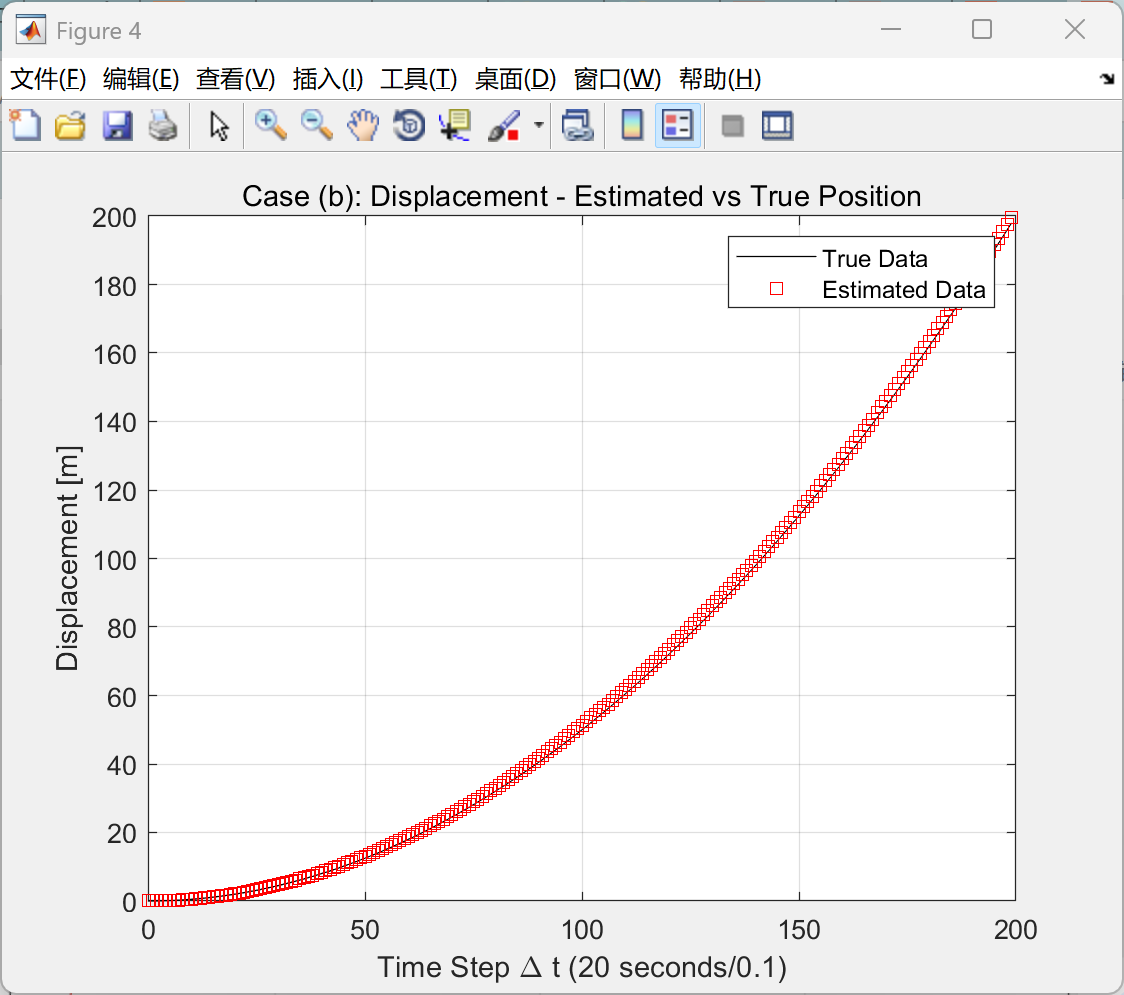
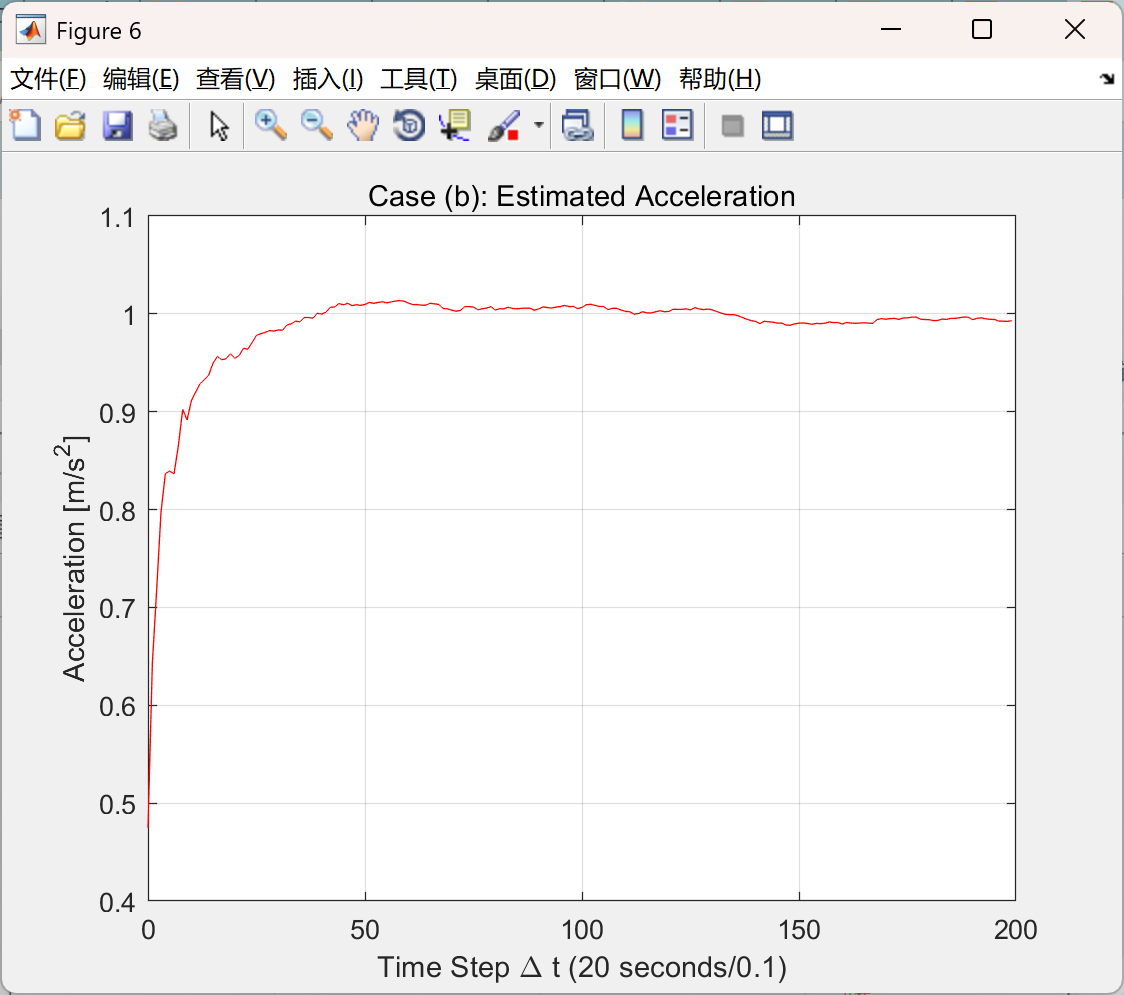
主函数部分代码：


close all
clear
clc

load('sen_pos_data2018.mat')
load('sen_tru_pos_data2018.mat')
load('sen_acc_data2018.mat')
% Matrix Definitions
T = 0.1;
sigma = 0.3;
F = [1 T (T^2)/2; 0 1 T; 0 0 1];
Q = (sigma^2)*[(T^4)/4 (T^3)/2 (T^2)/2; (T^3)/2 2*T^3 T^2;...
    (T^2)/2 T^2 T^2];
H = [1 0 0];
z = y;
a = y1;
X = [0; 0; 0];
P = [1 0 0; 0 1 0; 0 0 1];
R = 0.7;
I = eye(3);

% Displacement as measured value
for t = 1:200
    Xe = F*X;
    Pe = F*P*F' + Q;
    
    K = Pe*H'*inv(H*Pe*H' + R);
    Xu = Xe + K*(z(t) - H*Xe);
    Pu = (I - K*H)*Pe;
    
    XP(t) = Xu(1);
    VP(t) = Xu(2);
    AP(t) = Xu(3);
    X = Xu;
    P = Pu;
end
C=[XP; x];
figure(1)
plot((0:199),x,'-k')
hold on
plot((0:199),XP,'sr')
grid on
title('Case (a): Displacement - Estimated vs True Position')
xlabel('Time Step \Delta t (20 seconds/0.1)')
ylabel('Displacement [m]')
legend('True Data','Estimated Data')

figure(2)
plot((0:199),VP,'-r')
title('Case (a): Estimated Velocity')
grid on
xlabel('Time Step \Delta t (20 seconds/0.1)')
ylabel('Velocity [m/s]')

figure(3)
plot((0:199),AP,'-r')
title('Case (a): Estimated Acceleration')
grid on
xlabel('Time Step \Delta t (20 seconds/0.1)')
ylabel('Acceleration [m/s^2]')

% Acceleration as measured value
T = 0.1;
sigma = 0.1;
F = [1 T (T^2)/2; 0 1 T; 0 0 1];
Q = (sigma^2)*[(T^4)/4 (T^3)/2 (T^2)/2; (T^3)/2 2*T^3 T^2;...
    (T^2)/2 T^2 T^2];               % Process Noise
H = [0 0 1];
X = [0; 0; 0];
P = [1 0 0; 0 1 0; 0 0 1];          % Covariance Matrix
R = 0.9;
for t = 1:200
    Xe = F*X;                       % Status Prediction
    Pe = F*P*F' + Q;                % Covariance Prediction
    
    K = Pe*H'*inv(H*Pe*H' + R);     % Kalman Gain
    Xu = Xe + K*(y1(t) - H*Xe);     % State Update
    Pu = (I - K*H)*Pe;              % Covariance Update
    
    XP(t) = Xu(1);                  % Displacement
    VP(t) = Xu(2);                  % Velocity
    AP(t) = Xu(3);                  % Acceleration
    X = Xu;                         % State Reassignment
    P = Pu;                         % Covariance Reassignment
end
C1=[XP; x];

figure(4)
plot((0:199),x,'-k')
hold on
plot((0:199),XP,'sr')
grid on
title('Case (b): Displacement - Estimated vs True Position')
xlabel('Time Step \Delta t (20 seconds/0.1)')
ylabel('Displacement [m]')
legend('True Data','Estimated Data')

figure(5)
plot((0:199),VP,'-r')
grid on
title('Case (b): Estimated Velocity')
xlabel('Time Step \Delta t (20 seconds/0.1)')
ylabel('Velocity [m/s]')

figure(6)
plot((0:199),AP,'-r')
grid on
title('Case (b): Estimated Acceleration')
xlabel('Time Step \Delta t (20 seconds/0.1)')
ylabel('Acceleration [m/s^2]')