💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
使用 UBW 雷达监测 VMAT 治疗实施期间呼吸运动的 ANN 概述 在现代放射治疗领域,尤其是容积旋转调强放疗(VMAT)技术蓬勃发展的当下,精准监测患者在治疗过程中的呼吸运动至关重要。超宽带(UBW)雷达与人工神经网络(ANN)的结合为此提供了一种极具创新性与潜力的解决方案。
一、背景与意义
VMAT 治疗过程中,患者的呼吸运动会导致肿瘤及周围正常组织的位置发生动态变化。若不能精准跟踪这些位移,射线照射可能出现偏差,一方面无法对肿瘤给予充分剂量的辐射,影响治疗效果;另一方面,可能误照射到更多正常组织,引发不必要的副作用。传统的监测方法如体表标记追踪、呼吸带测量等存在一定局限性,例如对细微运动感知不灵敏、易受患者体表状态影响等。而 UBW 雷达技术凭借其独特的优势进入视野,它能够穿透衣物、被褥等介质,发射超宽带信号并接收因人体呼吸运动引起的反射波变化,实时、非侵入性地获取呼吸运动信息。将 UBW 雷达采集的数据进一步利用 ANN 进行深度处理,则有望克服传统分析方法的不足,实现对呼吸运动更精准、智能的监测。
二、UBW 雷达工作原理
UBW 雷达工作时,发射机持续发射纳秒级或皮秒级的超短脉冲信号,这些信号具有极宽的频谱带宽。当信号遇到人体时,因呼吸运动致使胸部、腹部等部位的体表产生微小位移,进而反射回雷达接收机的信号会在频率、相位、幅度等方面发生变化。通过对这些回波特性的分析,雷达系统能够提取出呼吸运动的相关参数,如呼吸频率、深度、幅度变化趋势等。其优势在于能够在不接触患者身体的前提下,提供连续、实时的呼吸数据,且不受光线、温度等外界环境因素干扰,适应放疗室的复杂环境。
三、ANN 在其中的作用
人工神经网络(ANN)作为一种模拟人类大脑神经元结构与功能的计算模型,在处理复杂、非线性数据关系方面表现卓越。在此应用场景下,ANN 接收由 UBW 雷达传来的原始呼吸运动数据,首先进行数据预处理,包括降噪、归一化等操作,提高数据质量。接着,通过构建包含输入层、隐藏层和输出层的多层神经网络架构,利用大量已标注的呼吸运动样本数据对网络进行训练。训练过程中,ANN 不断学习呼吸运动模式与特征之间的内在联系,例如不同呼吸阶段的波形变化规律、呼吸异常与疾病状态的关联等。一旦训练完成,ANN 便能对实时输入的雷达监测数据进行快速分析,精准预测呼吸运动的后续走势,提前判断可能出现的呼吸异常情况,为 VMAT 治疗设备的实时调整提供关键依据。
四、系统实现流程
首先,在 VMAT 治疗室内合理安装 UBW 雷达设备,确保其能够全方位、稳定地覆盖患者身体的呼吸运动监测区域,完成发射与接收信号的硬件搭建。然后,将雷达采集的数据传输至配套的计算机系统,运行预先构建并训练好的 ANN 模型。在治疗过程中,雷达持续采集呼吸数据,ANN 实时分析处理,一旦发现呼吸运动偏离正常范围或出现异常波动,立即向 VMAT 治疗控制系统发送预警信号,促使治疗设备暂停照射或调整射线参数,保障治疗的精准与安全。
五、优势与前景
这套基于 UBW 雷达与 ANN 的呼吸运动监测系统具有显著优势。一方面,它极大地提高了呼吸运动监测的精度与实时性,能够为 VMAT 治疗提供更可靠的运动补偿依据,提升肿瘤治愈率;另一方面,其非侵入性特点改善了患者的治疗体验,减少因监测设备带来的不适感。展望未来,随着技术的不断进步,UBW 雷达的性能将进一步优化,探测精度更高、范围更广;ANN 模型也将更加智能,能够适应更多复杂的个体差异和病情变化,为放射治疗的精准化、智能化发展注入强大动力,推动整个放疗领域迈向新的台阶。 以上内容你可根据实际需求进一步调整,若还有补充信息或修改意见,欢迎随时交流。
📚2 运行结果
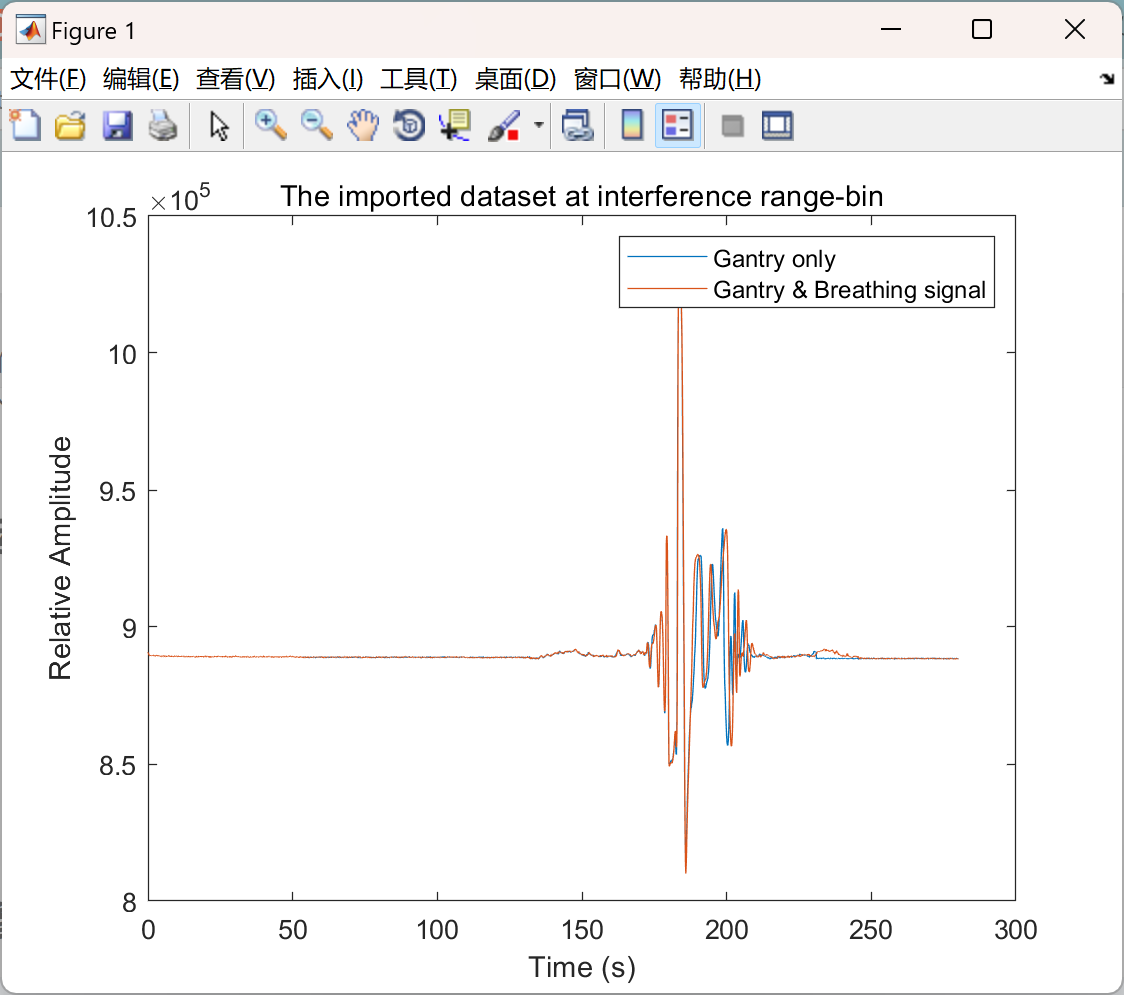
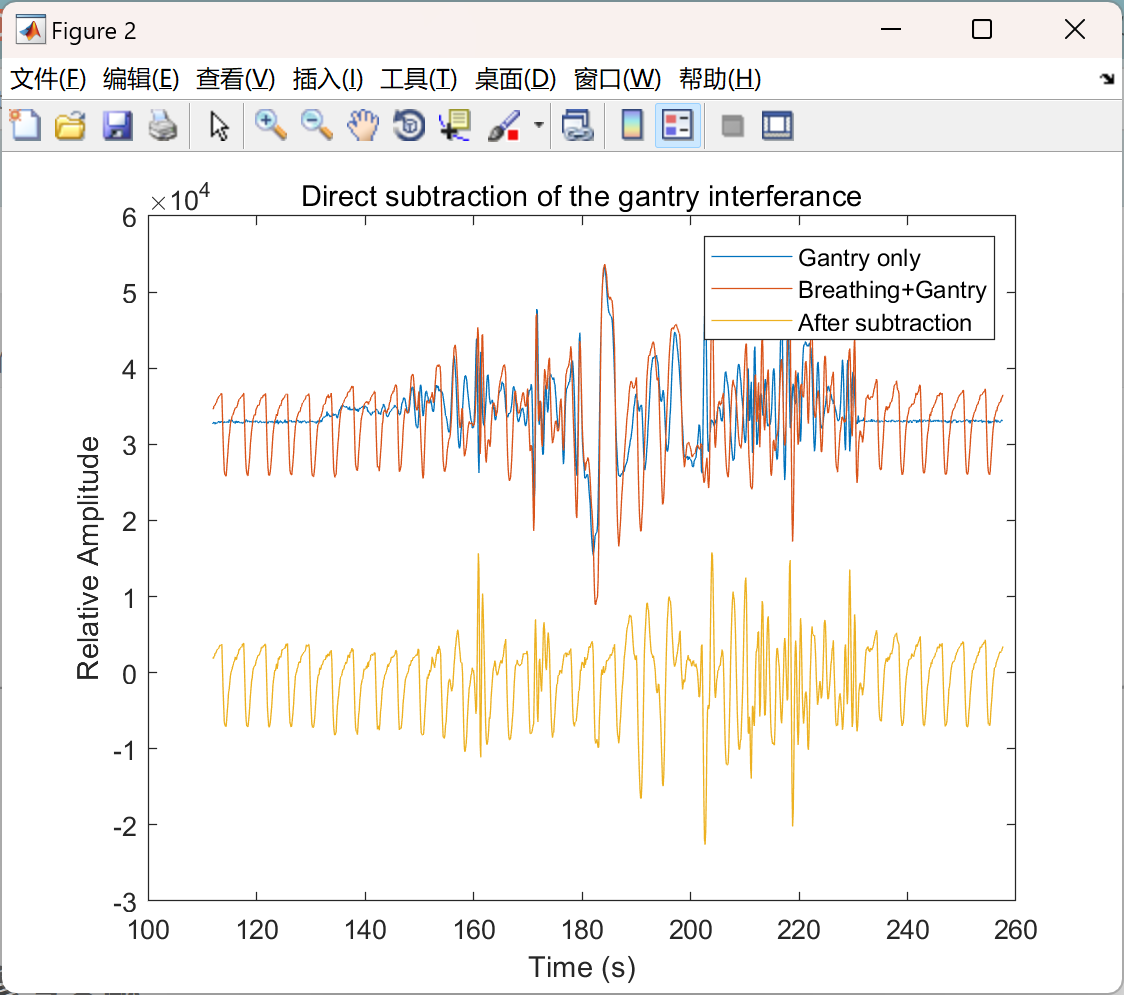
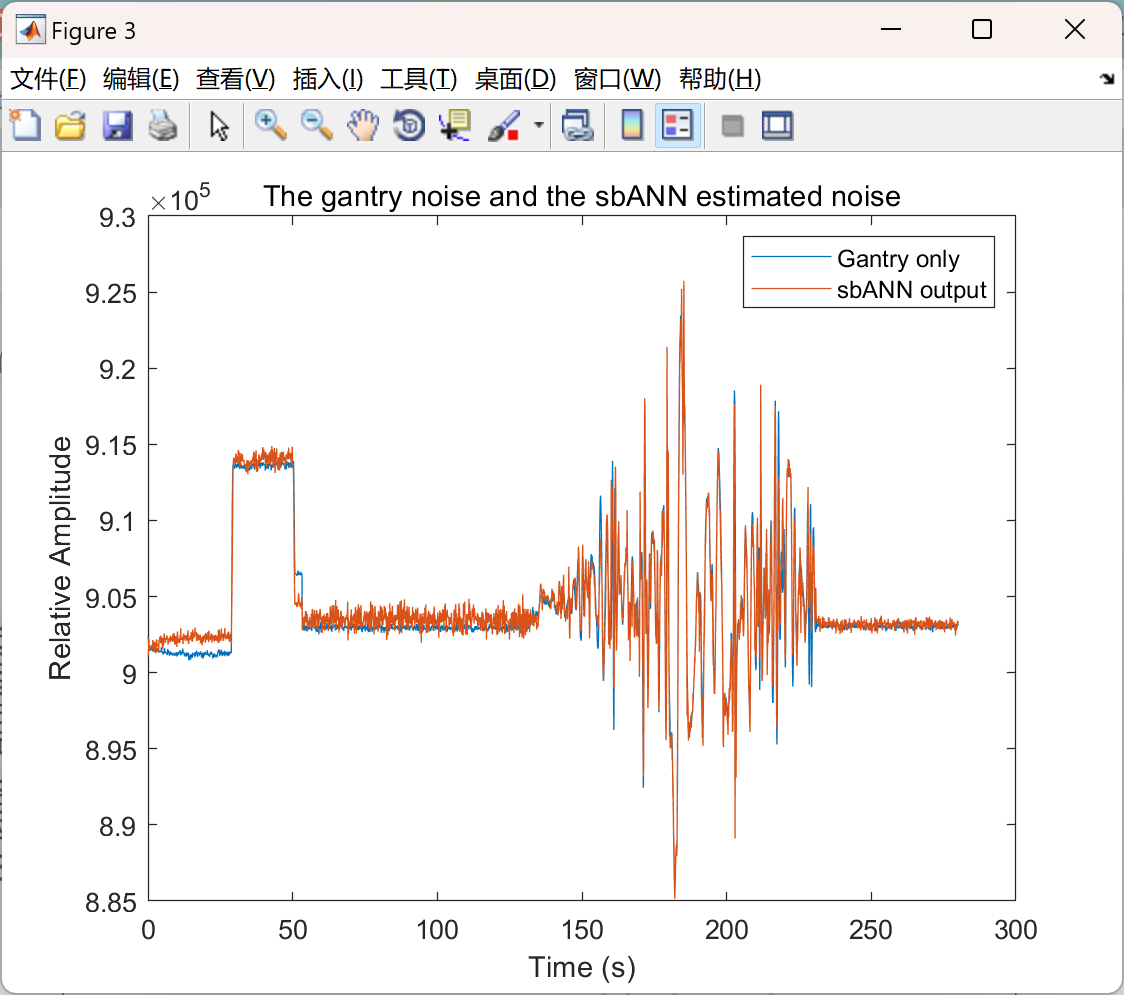
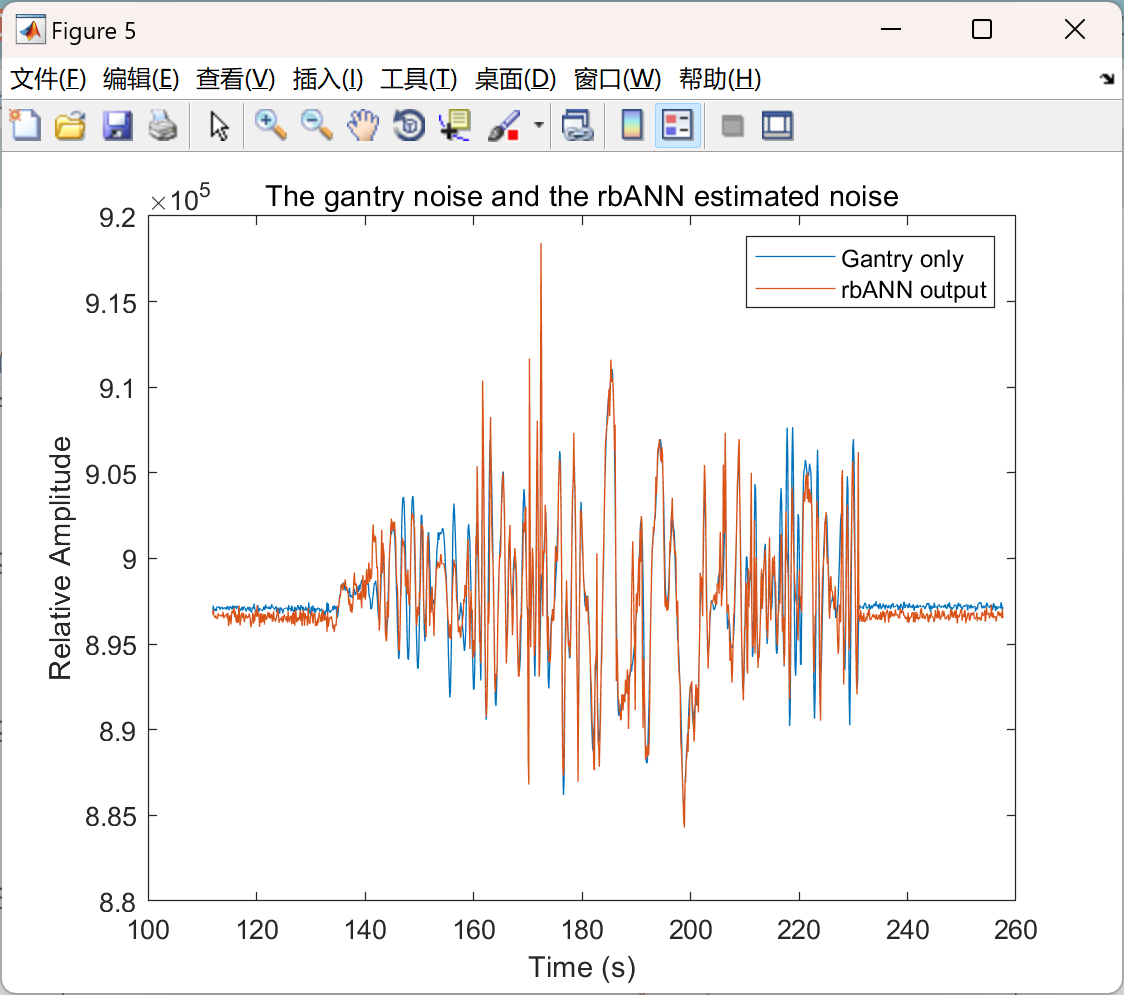
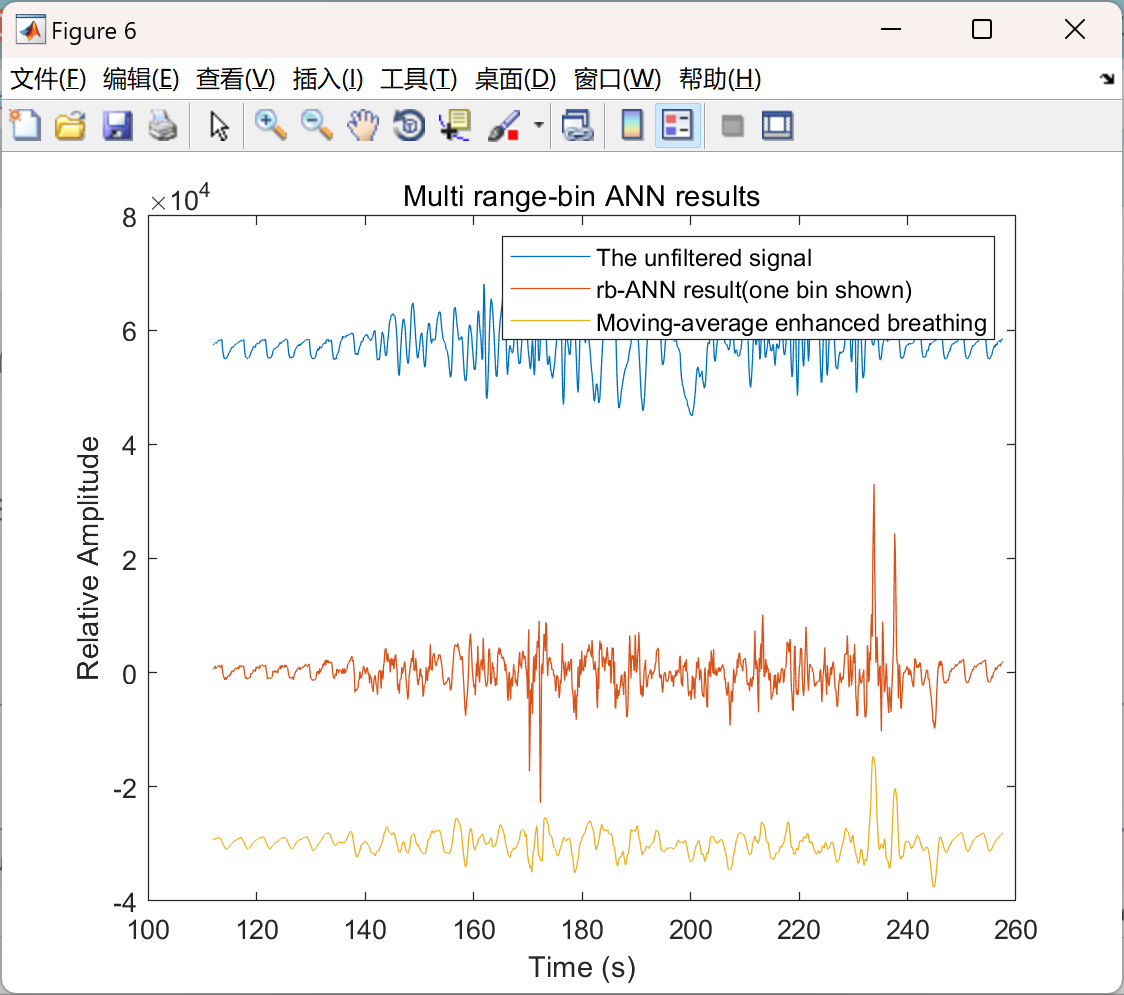
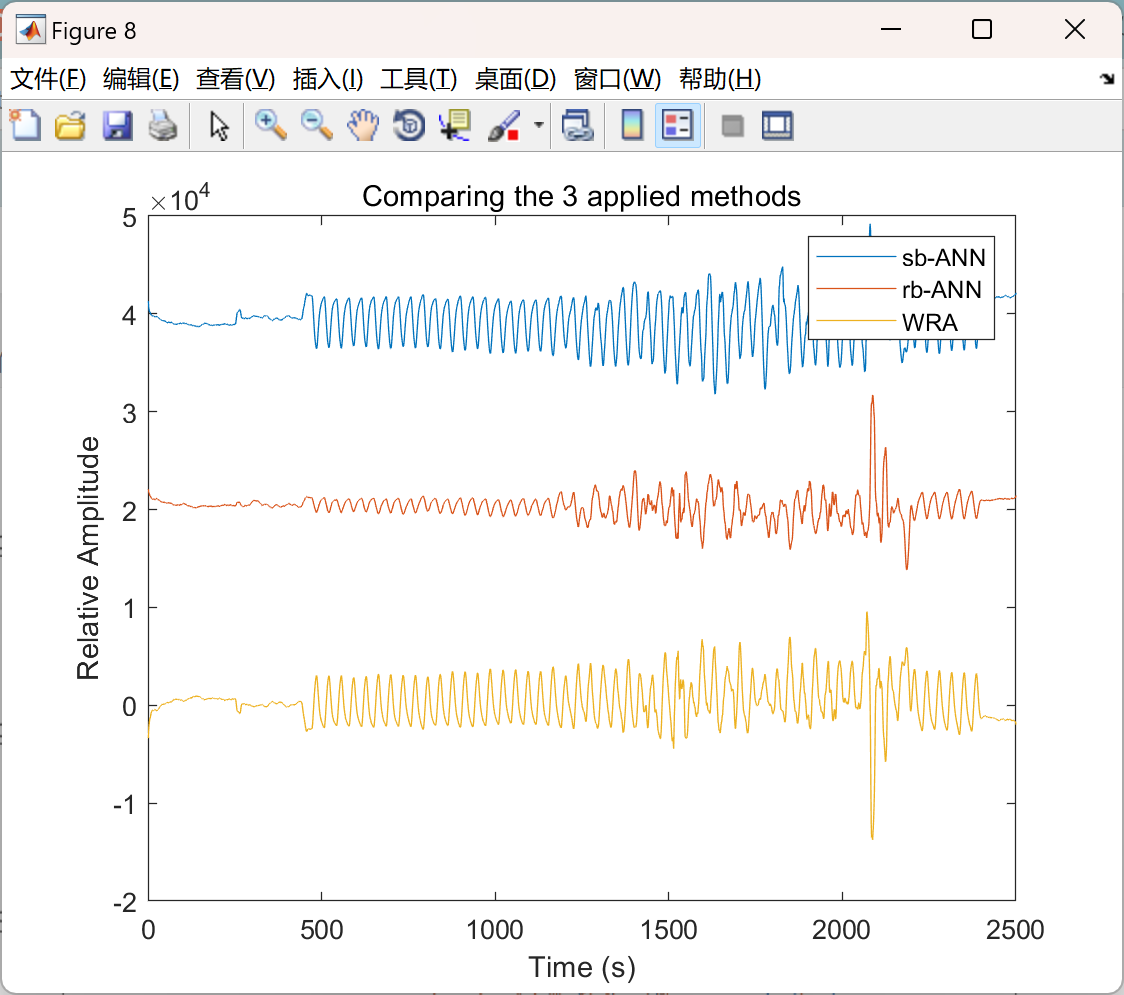
主函数部分代码:
set(0,'defaultfigurecolor',[1 1 1])
clear, close all
addpath Sub
%rng('default')
%% DATA COLLECTION --------------------------------------------------------
% Topology parameters
K_class = 2;
sample_rate = 1;
meter_pixel = 9;
map_height = 50; % Drone height for air-to-ground power map
sample_height = 50; % Drone height for learning (Learning stage)
neighbour_mat = [0 0; -1 0; 0 -1; 1 0; 0 1] * 39; %
neighbour_weight = [0.6; 0.1; 0.1; 0.1; 0.1]; % Sum-to-one
test_positions = round(1:100);
noise_guass = 3; % dB std
n_ue = 50; % [8*8 9*10 11*11 13*13 15*16 18*18 21*22 25*26 30*30 35*36]*8
n_uav = 50 * length(sample_height); % 15:50:9 50:200:5 100:400
n_mea = n_ue * n_uav;
n_uav = round(n_uav / length(sample_height));
residual_on = false;
residsec_on = false;
residthi_on = false;
residfou_on = false;
residfiv_on = true;
segment_on = false;
segresid_on = false;
plot_on = false;
kmeans_on = false;
% DATA = load('radiomap_shanghai100tx_2.5GHz.mat');
% DATA = load('radiomap_simulated100tx_noise.mat');
% DATA = load('radiomap_shanghai115tx_28GHz.mat');
% DATA = load('radiomap_simulated100tx_nonoise');
DATA = load('radiomap_simulated100tx_3class.mat');
pos_ue = DATA.PosUE;
Xdata = zeros(n_mea, 6);
Gdata = zeros(n_mea, 1);
Ddata = zeros(n_mea, 1);
Gtrue = cell(n_ue, 1);
cnt = 0;
figure(1)
title("Users' locations")
hold on
pos_ue_all = zeros(size(pos_ue));
userids = sort(randperm(length(pos_ue), n_ue));
for id = 1:length(userids)
% i must increase
i = userids(id);
% Training data
for j = 1:length(sample_height)
uav_height = sample_height(j);
x = pos_ue(i,1); y = pos_ue(i,2); z = pos_ue(i,3);
I = (DATA.RadioMap(:, 6) == uav_height) ...
& (DATA.RadioMap(:, 1) == x) ...
& (DATA.RadioMap(:, 2) == y)...
& (DATA.RadioMap(:, 3) == z);
Rm2D = DATA.RadioMap(I, :);
Xvec = Rm2D(:, 4); Yvec = Rm2D(:, 5); Zvec = Rm2D(:, end);
[Xmat,Ymat] = meshgrid((min(Xvec):5:max(Xvec)),(min(Yvec):5:max(Yvec)));
Zmat = griddata(Xvec, Yvec, Zvec, Xmat, Ymat);
position = [x-min(Xvec)+1 y-min(Yvec)+1 z];
Xmat = Xmat - min(Xvec) + 1;
Ymat = Ymat - min(Yvec) + 1;
% Data pre-processing
Zmat(isnan(Zmat)) = min(min(Zmat));
Zmat = Zmat + randn(size(Zmat)) * noise_guass;
Xvec = Xmat(:);
Yvec = Ymat(:);
Zvec = Zmat(:);
dist = log10(vecnorm([Xvec Yvec uav_height*ones(length(Xvec),1)] - ...
ones(length(Xvec),3).*position, 2, 2));
position = [ceil(position(1:2)) z];
if ~exist('idx', 'var')
%idx = 1:ceil(length(Xvec)/nDrone):length(Xvec);
idx = randperm(length(Xvec), n_uav);
end
uav_positon = ceil([Xvec(idx) Yvec(idx)]);
uav_num = length(uav_positon);
cnt = cnt + uav_num;
Xdata(cnt-uav_num+1:cnt, :) = [uav_positon ...
uav_height.*ones(uav_num,1) ones(uav_num,3).*position];
Gdata(cnt-uav_num+1:cnt, :) = Zvec(idx);
Ddata(cnt-uav_num+1:cnt, :) = dist(idx);
figure(1)
plot(position(1), position(2), '.');
text(position(1), position(2), string(i));
pos_ue_all(i, :) = position;
end
% Test data
uav_height = map_height;
x = pos_ue(i,1); y = pos_ue(i,2); z = pos_ue(i,3);
I = (DATA.RadioMap(:, 6) == uav_height) ...
& (DATA.RadioMap(:, 1) == x) ...
& (DATA.RadioMap(:, 2) == y)...
& (DATA.RadioMap(:, 3) == z);
Rm2D = DATA.RadioMap(I, :);
Xvec = Rm2D(:, 4); Yvec = Rm2D(:, 5); Zvec = Rm2D(:, end);
[Xmat,Ymat] = meshgrid((min(Xvec):5:max(Xvec)),(min(Yvec):5:max(Yvec)));
Zmat = griddata(Xvec, Yvec, Zvec, Xmat, Ymat);
position = [x-min(Xvec)+1 y-min(Yvec)+1 z];
Xmat = Xmat - min(Xvec) + 1;
Ymat = Ymat - min(Yvec) + 1;
% Data pre-processing
Xvec = Xmat(:);
Yvec = Ymat(:);
Zvec = Zmat(:);
Zmat(isnan(Zmat)) = min(Zvec);
Gtrue{i} = Zmat;
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
[1]Park Y J ,Lee Y ,Choi W Y , et al.Author Correction: Preclinical Evaluation of a Noncontact Simultaneous Monitoring Method for Respiration and Carotid Pulsation Using Impulse-Radio Ultra-Wideband Radar[J].Scientific Reports,2024,14(1):20350-20350.
[2]Mehrjouseresht P ,Hail E R ,Karsmakers P , et al.Respiration and Heart Rate Monitoring in Smart Homes: An Angular-Free Approach with an FMCW Radar.[J].Sensors (Basel, Switzerland),2024,24(8):
🌈4 Matlab代码实现





















 668
668

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








