【路径搜索】在灰度地图上搜索从 A 点到 B 点的最低成本路径（Matlab实现）

最新推荐文章于 2025-01-11 08:42:11 发布

原创最新推荐文章于 2025-01-11 08:42:11 发布 · 799 阅读

29 ·

CC 4.0 BY-SA版权

文章标签：

#人工智能 #前端 #算法

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

💥1 概述

在灰度地图上搜索从 A 点到 B 点的最低成本路径，通常涉及到将图像处理技术与路径规划算法相结合。这种类型的路径规划问题常见于机器人导航、无人驾驶车辆等领域，其中灰度地图可以表示环境的不同特征，如地形难度、障碍物位置或移动成本等。

1. 灰度地图解释

灰度值：灰度地图中的每个像素点都有一个灰度值，这个值可以用来表示该位置的成本（例如，越亮的区域可能代表越高的成本）。
成本建模：通过定义规则，将灰度值转换为实际的运动成本，比如穿越某个区域所需的能量消耗、时间或者风险。

2. 地图预处理

二值化/阈值化：如果需要简化问题，可以将灰度地图转化为二值地图（黑白），其中白色像素表示可通行区域，黑色像素表示障碍物。
滤波和噪声去除：应用滤波器来平滑图像，减少不必要的细节和噪音，以提高路径搜索效率。

3. 路径搜索算法

A* (A-star) 算法：结合启发式估计与实际成本，快速找到一条从起点到终点的低成本路径。
Dijkstra 算法：保证找到最短路径，但计算量较大，适合用于小型或静态地图。
RRT (Rapidly-exploring Random Trees)** 和 PRM (Probabilistic Roadmap)：适用于高维空间或复杂环境下的路径搜索。

4. 成本函数设计

启发式函数：对于像A*这样的算法，设计一个好的启发式函数可以帮助更快地找到近似解。这通常是基于欧几里得距离或其他形式的距离度量。
累积成本：随着路径延伸，累积路径上的所有成本，确保最终选择的是总成本最低的路径。

5. 实施步骤

1. 初始化：设置起始点 A 和目标点 B，并初始化开放列表（包含待探索节点）和关闭列表（已经探索过的节点）。
2. 迭代搜索：从起始点开始，按照选定的算法逐步扩展搜索范围，直到找到到达目标点 B 的路径或确定没有可行路径为止。
3. 路径优化：一旦找到初步路径，可以通过进一步优化减少路径长度或降低整体成本。
4. 结果输出：输出最终权重最小的路径，同时可以可视化路径在原始灰度地图上的表现。

6. 应用实例

在实际应用中，这种方法可以被应用于多种场景，如无人机航拍路线规划、自动导引车(AGV)路径选择以及虚拟角色在游戏世界中的智能导航等。通过上述步骤，可以在给定的灰度地图上有效地执行从 A 点到 B 点的最低成本路径搜索。重要的是要根据具体的应用需求调整算法参数和成本模型，以获得最佳性能。

📚2 运行结果

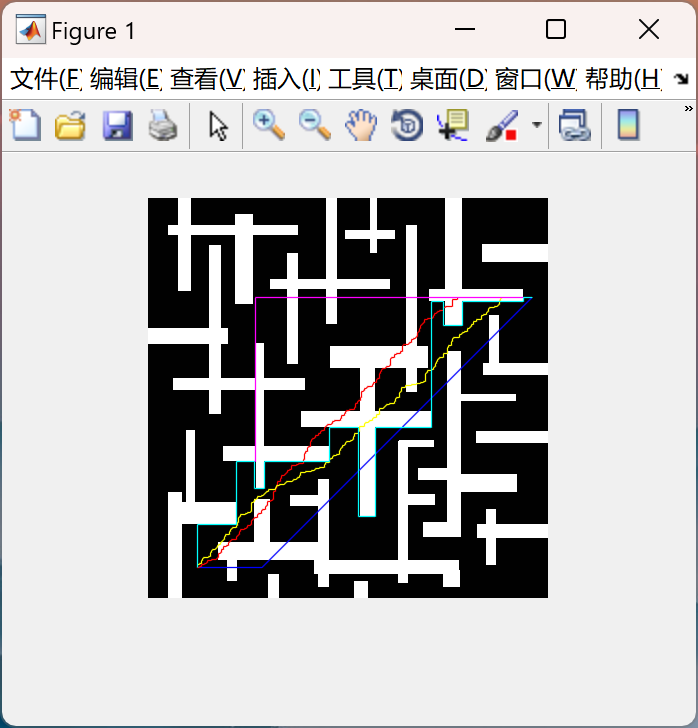
主函数部分代码：

clear all
close all;
clc

% Load a map
Map = MapPreparation('Maps/Map2.png');

Start =[50,370];
Goal = [385,100];

% Define a time limit
Time = 5;

TimeObtained = [];

% Start one of functions (straight line)
fprintf('\nTesting simple algorithm\n');
SolutionTimer = tic;                                            % Start timer
VectSimple = A_SimpleAlgorithm(Map,Time,Start,Goal) ;          % Start the algorithm
TimeObtained(1) = toc(SolutionTimer);
if(TimeObtained(1) > Time)                                      % Check if time limit was exceeded
    fprintf('Time exceeded\n');
else end

% Start second function (random algorithm)
fprintf('\nTesting random algorithm\n');
SolutionTimer = tic; 
VectRandom = A_RandomAlgorithm(Map,Time,Start,Goal);
TimeObtained(2) = toc(SolutionTimer);
if(TimeObtained(2) > Time)
    fprintf('Time exceeded\n');
else end

% Start third function (random algorithm that utilizes full time avilable)
fprintf('\nTesting random algorithm with time control\n');
SolutionTimer = tic; 
VectRC = A_RandomControl(Map,Time,Start,Goal);
TimeObtained(3) = toc(SolutionTimer);
if(TimeObtained(3) > Time)
    fprintf('Time exceeded\n');
else end

% Start fourth function (directed algorithm - choice of better option out of two)
fprintf('\nTesting directed algorithm\n');
SolutionTimer = tic; 
VectDS = A_DirectedSimpleAlgorithm(Map,Time,Start,Goal);
TimeObtained(4) = toc(SolutionTimer);
if(TimeObtained(4) > Time)
    fprintf('Time exceeded\n');
else end

% % Start fifth function (A lazy algorithm that generates simple trajectory
% % but in 10 seconds)
% fprintf('\nTesting lazy algorithm\n');
% SolutionTimer = tic; 
% VectLazy = A_LazyAlgorithm(Map,Time,Start,Goal);
% TimeObtained(5) = toc(SolutionTimer);
% if(TimeObtained(5) > Time)
%     fprintf('Time exceeded\n');
% else end

fprintf('\nTesting Krol_Mucha algorithm\n');
SolutionTimer = tic; 
VectorOur = A_Krol_1(Map,Time,Start,Goal);
TimeObtained(5) = toc(SolutionTimer);
if(TimeObtained(5) > Time)
    fprintf('Time exceeded\n');
else end