【滤波跟踪】使用卡尔曼滤波的 2D 对象跟踪（Matlab实现）

原创已于 2024-04-22 16:26:05 修改 · 352 阅读

7 ·

CC 4.0 BY-SA版权

文章标签：

#matlab #开发语言

于 2024-04-22 16:20:02 首次发布

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

💥1 概述

使用卡尔曼滤波进行2D对象跟踪是一种常见的方法，特别适用于动态系统中目标位置的估计和预测。首先，需要对目标进行初始化，包括确定初始位置、速度和加速度等状态信息，以及建立系统模型和测量模型。当新的测量值可用时，利用测量模型对预测状态进行修正，通过测量值与预测值之间的残差来更新状态估计，并优化状态的不确定性。通过使用卡尔曼滤波进行2D对象跟踪，可以实现对运动目标的准确估计和预测，从而在复杂环境中实现可靠的目标跟踪和定位。

📚2 运行结果

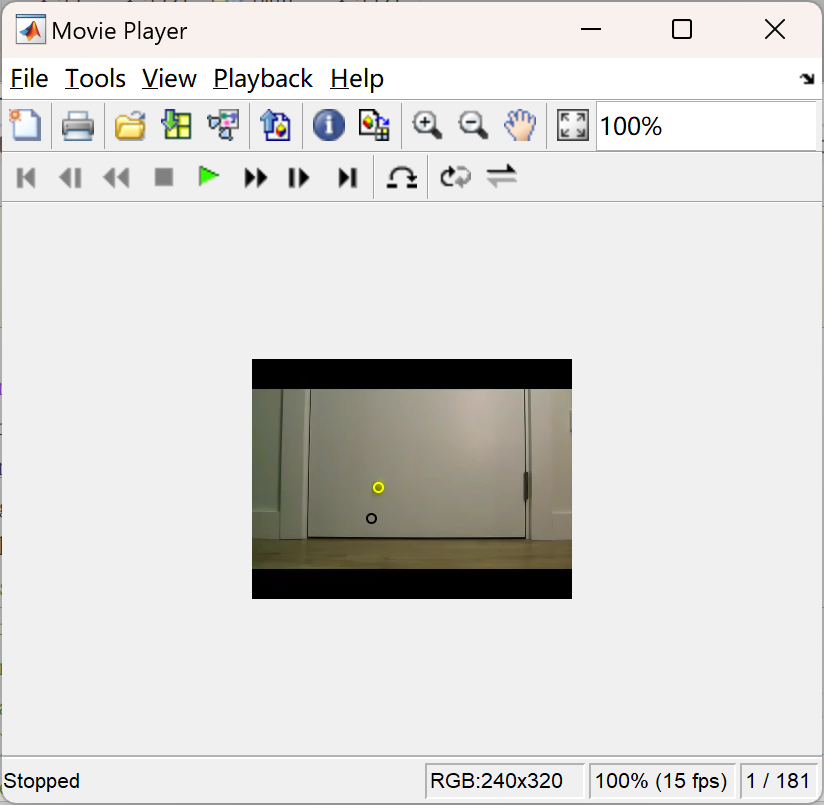
主函数部分代码：

clc; 
clear all;
close all;
%% Video Initialization
video_name = 'sample3.mp4'; %Video name
vid = VideoReader(video_name); 
nframes = vid.NumberOfFrames; %Number of frames
Height = vid.Height; % Height :)
Width = vid.Width; % Width :)
thr = 10; % Threshold for generating binary image of the noise
%% Kalman Filter Definition
% First, we define the state of interest. In this case, we define the
% following variables for our states: state(t) = [X Y dx dy (d^2)x (d^2)y](t)
% X(t+1) = 1/2(a)T^2 + V(t)T + X(t); where a and V denotes the acceleration
% and velocity respectively.
% V(t+1) = aT + V(t)
% a(t+1) = a(t) ; assuming constant acceleration 
%State(t+1) = A.State(t) + B.u + <State Uncertainty|State Noise>
dt=0.5;
% A = [1 0 dt 0 (dt^2)/2 0;
%      0 1 0  dt 0    (dt^2)/2;
%      0 0 1  0  dt    0;
%      0 0 0  1  0     dt;
%      0 0 0  0  1     0;
%      0 0 0  0  0     1];
A = [1 0 dt 0;
     0 1 0 dt;