💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
摘要:
我们提出了一种分区化方法,用于找到符合动态随机模型并通过嘈杂测量观察的潜在时间序列的最大后验(MAP)估计。我们特别考虑具有非马尔可夫信号动态(例如,群稀疏性)和/或非高斯测量模型(例如,神经科学中使用的点过程观测模型)的现代信号处理问题。通过在MAP估计问题中使用辅助变量,我们展示了交替方向乘法器的共识形式,使得可以通过迭代基于似然和先验计算单独的估计,并随后以适当的方式使用卡尔曼平滑器“平均”它们。因此,这可以应用于广泛的问题设置,并且仅在交换统计模型的各个方面时需要模块化调整。在广泛的对数凹性假设下,我们展示了单独的估计问题是凸优化问题,并且迭代算法收敛到MAP估计。因此,这个框架可以捕捉非马尔可夫潜在时间序列模型和非高斯测量模型。我们提供了示例应用,涉及:1)在电生理谱时空估计的背景下使用群稀疏先验,以及2)在使用神经尖峰和行为观察进行学习动态分析的背景下使用非高斯测量模型。
我们考虑基于潜在动态模型和噪声测量估计潜在时间序列的问题。这样的问题出现在各种环境中,包括(但不限于)跟踪[1]、医学成像[2]和视频去噪[3]。考虑到这个问题表述的广泛适用性,所使用的基础模型不可避免地变得越来越复杂。
某些场景已经得到深入研究,比如线性系统与高斯噪声的情况,众所周知,最大后验(MAP)点估计可以通过卡尔曼平滑器(KS)[4]获得。在引入非线性因素时,可选的方法包括依赖于线性逼近的扩展卡尔曼滤波器(EKF),以及使用基于样本的技术的无迹卡尔曼滤波器(UKF)[5]和粒子滤波器(PF)[6]。虽然EKF和UKF非常适用于广泛的问题类别,但对于具有非高斯噪声的模型并不适用。这对于越来越受欢迎的将稀疏诱导模型纳入潜在信号估计的问题是有问题的。这些问题包括利用底层信号的稀疏性[7]–[10],以及利用信号动态的稀疏性[11]–[13]。虽然其中一些方法利用ℓ1正则化在局部层面实施稀疏性并实现因果预测,但通常存在全局结构的知识,例如群 lasso 偏好的结构,这些结构要求批量估计。在这种情况下,期望的估计问题与经典的状态估计问题有所偏离,因为底层信号不再是马尔可夫的。在这种情况下,没有明显的扩展可以用于解决底层信号的非马尔可夫性的 EKF、UKF 或 PF。
所讨论问题的广泛范围决定了对各种测量模型和系统模型进行潜在时间序列估计需要系统化方法。此外,一个能够将这两个模型分隔开的解决方案框架有助于互换性,并允许新的正则化技术轻松地纳入估计过程中。
我们开发了一个使用交替方向乘子法(ADMM)[15]的框架,根据温和的(即对数凹性)假设,对具有非马尔可夫潜在变量和/或非线性观测的问题提供 MAP 估计。虽然 ADMM 已被用于将特定动态系统分解为更简单的子问题[13],[16],但我们的方法适用于任意对数凹动态模型。具体而言,我们利用辅助变量使得解决方案涉及对三个模块的迭代更新,一个与测量模型相关,另一个与潜在信号的先验分布相关,第三个是卡尔曼平滑器。因此,我们的框架使得各种稀疏模型可以轻松应用于信号和/或动态,只需对应模块进行调整。我们在两个不同的应用中展示了框架的实现,即潜在状态估计和光谱时间估计。我们展示,在状态估计的情况下,我们的方法在两个与非高斯观测值相关的状态空间模型中优于固定间隔平滑器和粒子滤波器。在光谱时间估计的情况下,我们展示了在使用非马尔可夫先验时我们方法的有效性。所提出的方法为潜在过程估计提供了一种直观的方法,即通过迭代使用卡尔曼平滑器与标准凸优化技术相结合。我们通过证明我们的方法保证在适用于一般 ADMM 方法的相对温和条件下收敛到 MAP 解来提供对直觉的数学上的证明。最后,我们提供软件,使读者能够重现本文的结果,并轻松将框架应用于新模型。我们的贡献可以总结如下:
我们提出了一个高效的迭代解决方案框架,用于潜在时间序列估计,在温和的对数凹性假设下保证收敛到 MAP 估计。
在存在非线性、非高斯测量模型的情况下,我们的方法不需要高斯逼近,不像 KS 变体,并且比顺序蒙特卡洛(SMC)方法更高效。
我们的框架适用于非马尔可夫信号,尽管没有明确的方法可以适应这种情况,特别是当先验适用于潜在过程的高度非线性函数,例如奇异值分解。
通过使用辅助变量,我们对重新制定的 MAP 估计问题的 ADMM 解决方案是模块化的,观测和系统模型在不同的模块中,通过卡尔曼平滑器统一起来。
本文结构如下:第 II 节提供了我们正在解决的问题的一般公式,以及解决特定问题实例的相关工作的简要回顾。第 III 节详细介绍了解决 MAP 估计问题的新颖系统化方法。第 IV 节通过在两个现有问题上的实现展示了框架的能力。第 V 节通过讨论结果和未来工作总结了本文。
详细文章见第4部分。
📚2 运行结果
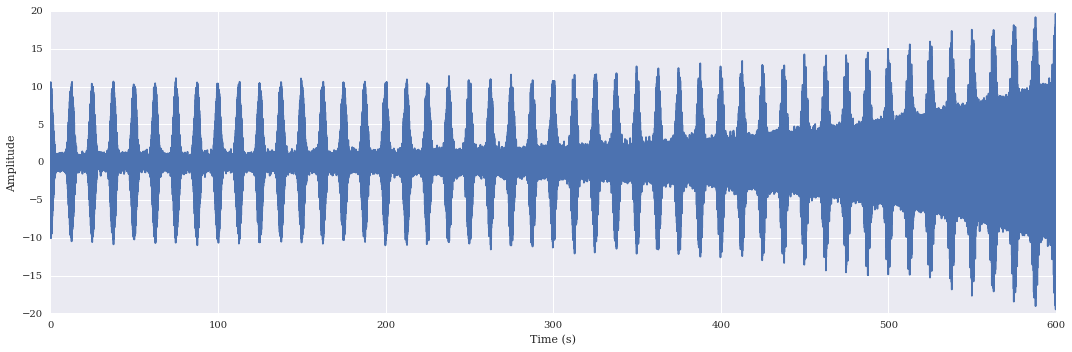
T = 600 #[s]
fs = 500 #[Hz]
f0 = 0.04 #[Hz]
f1 = 10 #[Hz]
f2 = 11 #[Hz]
noise_var = 1.0
t = np.linspace(0,T,fs*T)
signal = 10*(np.cos(2*np.pi*f0*t))**8*np.sin(2*np.pi*f1*t) + \
10*np.exp(4*(t-T)/T)*np.cos(2*np.pi*f2*t)
noise = np.random.normal(0,noise_var,T*fs)
signal = signal + noise
from scipy.signal import decimate
dec = 4
signal = decimate(signal,dec)
fs = fs//dec
plt.figure(figsize=(15,5))
plt.plot(np.linspace(0,T,len(signal)),signal)
plt.ylim([-20,20])
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')
plt.tight_layout();
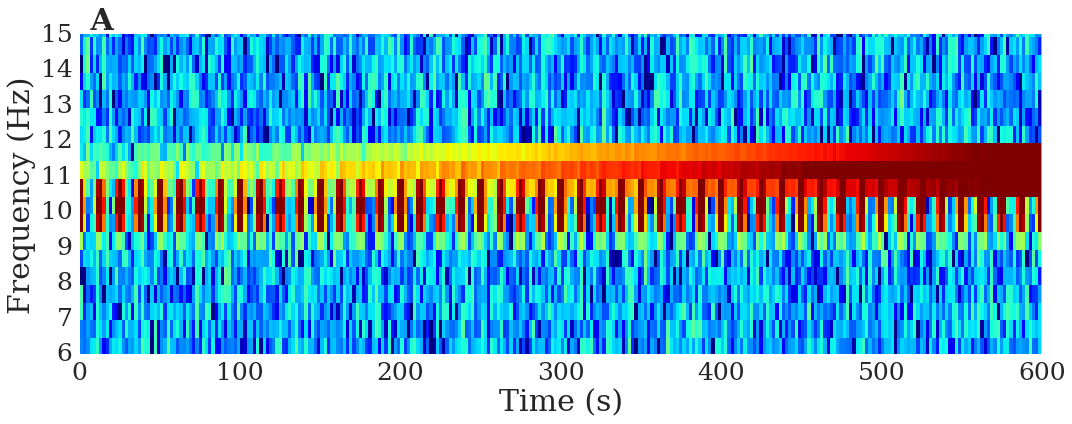
ig, ax = plt.subplots(figsize=(15,6))
im0 = ax.specgram(signal,NFFT=1000//dec,Fs=500//dec,noverlap=0,interpolation='nearest',aspect='auto')#,window=matplotlib.mlab.window_none)
ax.set_ylabel('Frequency (Hz)',fontsize=30)
ax.set_xlabel('Time (s)',fontsize=30)
im0[3].set_clim((-40,10))
ax.set_ylim([6,15])
ax.tick_params(axis='both', which='major', labelsize=25)
plt.grid('off')
plt.title(' A',loc='left',fontsize=30,weight='bold')
plt.tight_layout()
if save_figs: plt.savefig(fig_dir + 'sig_specgram.eps', format='eps', dpi=200)
plt.show()
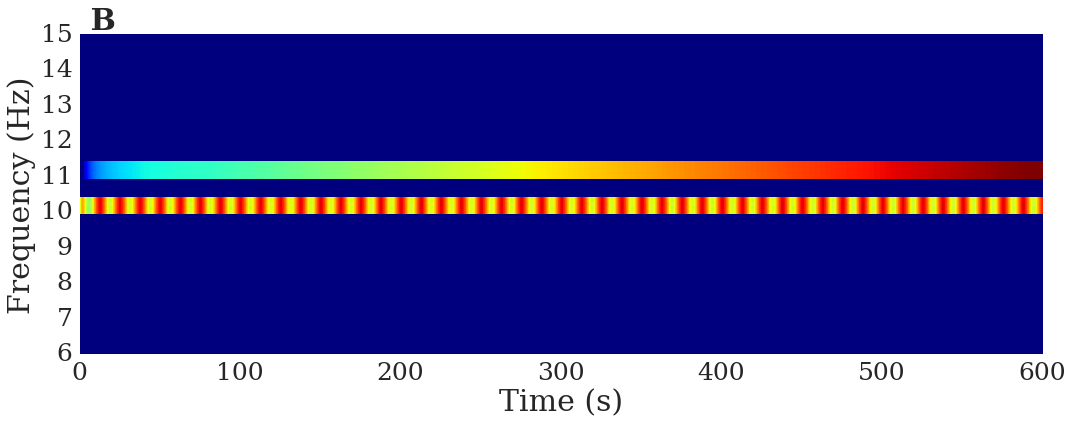
fig, ax = plt.subplots(figsize=(15,6))
x = x_spec_mag - np.max(x_spec_mag)+10
im1 = ax.imshow(x,origin='lower',vmin=-40,vmax=10,extent=(0,T,0,K//4),aspect='auto',interpolation='nearest')
ax.axis('tight')
ax.set_ylabel('Frequency (Hz)',fontsize=30)
ax.set_xlabel('Time (s)',fontsize=30)
ax.set_ylim([6,15])
ax.grid('off')
ax.tick_params(axis='both', which='major', labelsize=25)
plt.title(' B',loc='left',fontsize=30,weight='bold')
plt.tight_layout()
if save_figs: plt.savefig(fig_dir + 'sig_specpursuit.eps', format='eps', dpi=200)
plt.show()
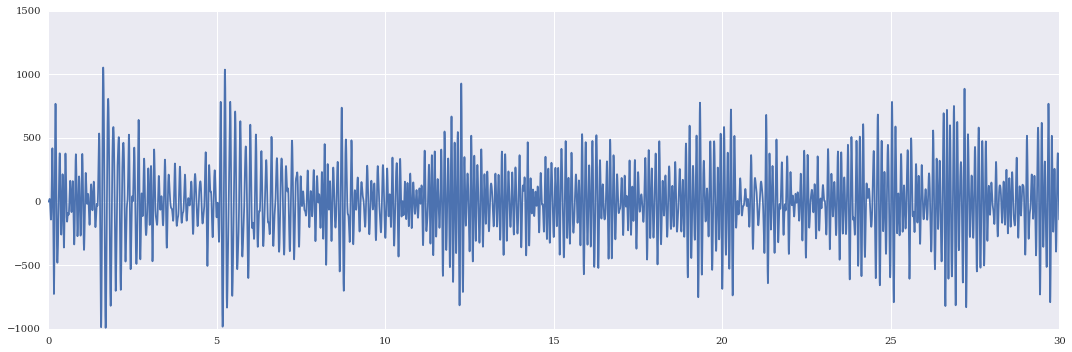
signal = sio.loadmat('../data/GO-N2-e3a.mat',squeeze_me=1)['new']
n = np.arange(len(signal))
fs = 500
nyq = 250
b,a = butter(6,[6/nyq,14/nyq],btype='band')
signal = lfilter(b,a,signal)
fig, ax = plt.subplots(figsize=(15,5))
plt.plot(n/fs,signal)
fig.tight_layout()
L = 256*4
noverlap = 0
coeffs,freqs,t = mlab.specgram(signal,NFFT=L,Fs=fs,noverlap=L*0.75,window=mlab.window_none)
coeffs = 10*np.log10(coeffs)
coeffs = coeffs - np.max(coeffs)
fig, ax = plt.subplots(figsize=(15,6))
im1 = ax.imshow(coeffs,origin='lower',extent=[0,len(signal)/fs,0,fs/2],aspect='auto',interpolation='nearest')
ax.set_ylabel('Frequency (Hz)',fontsize=30)
ax.set_xlabel('Time (s)',fontsize=30)
im1.set_clim(-20,0)
ax.set_ylim([6,14])
ax.grid('off')
ax.tick_params(axis='both', which='major', labelsize=25)
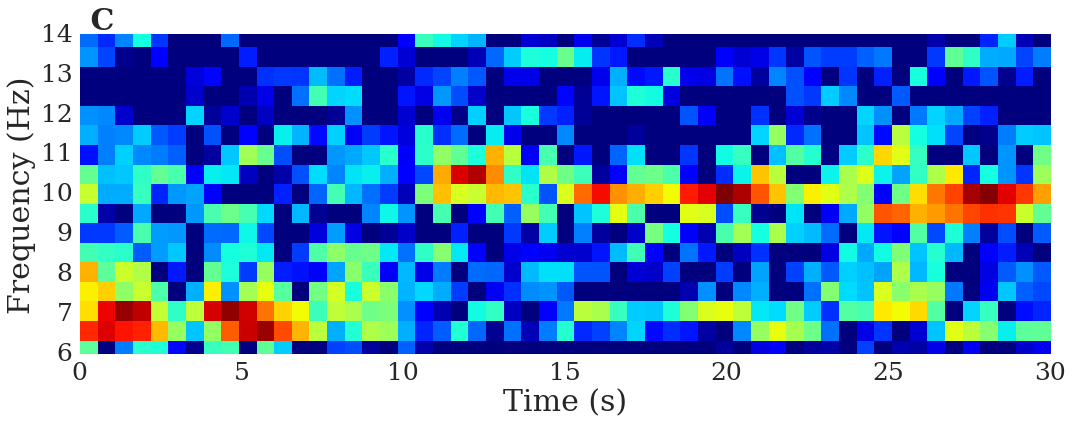
plt.title(' C',loc='left',fontsize=30,weight='bold')
plt.tight_layout()
if save_figs: plt.savefig(fig_dir + 'eeg_specgram.eps', format='eps', dpi=200)
plt.show()
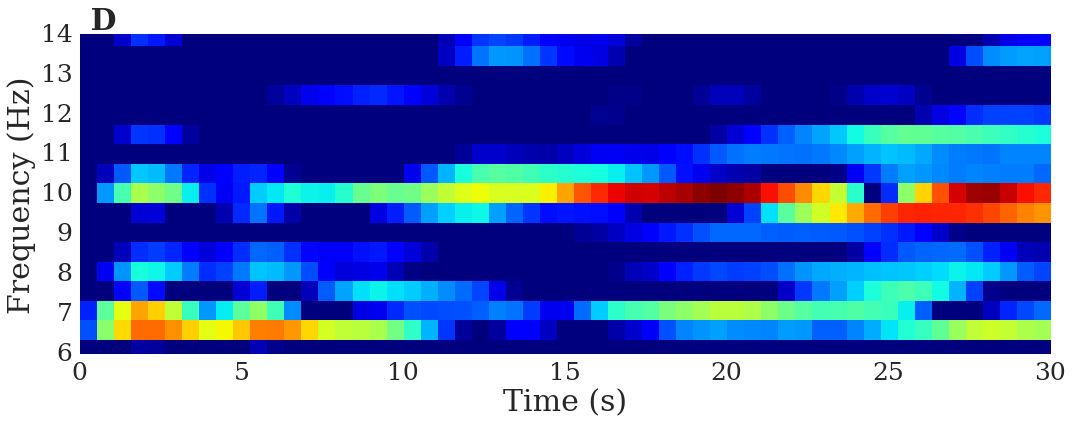
fig, ax = plt.subplots(figsize=(15,6))
im1 = ax.imshow(coeffs_mag,vmin=-20,vmax=0,origin='lower',extent=[0,len(signal)//fs,0,fs//2],aspect='auto',interpolation='nearest')
ax.axis('tight')
ax.set_ylim([6,14]);
ax.set_ylabel('Frequency (Hz)',fontsize=30)
ax.set_xlabel('Time (s)',fontsize=30)
ax.grid('off')
ax.tick_params(axis='both', which='major', labelsize=25)
plt.title(' D',loc='left',fontsize=30,weight='bold')
plt.tight_layout()
if save_figs: plt.savefig(fig_dir + 'eeg_lrsd.eps', format='eps', dpi=200)
plt.show()
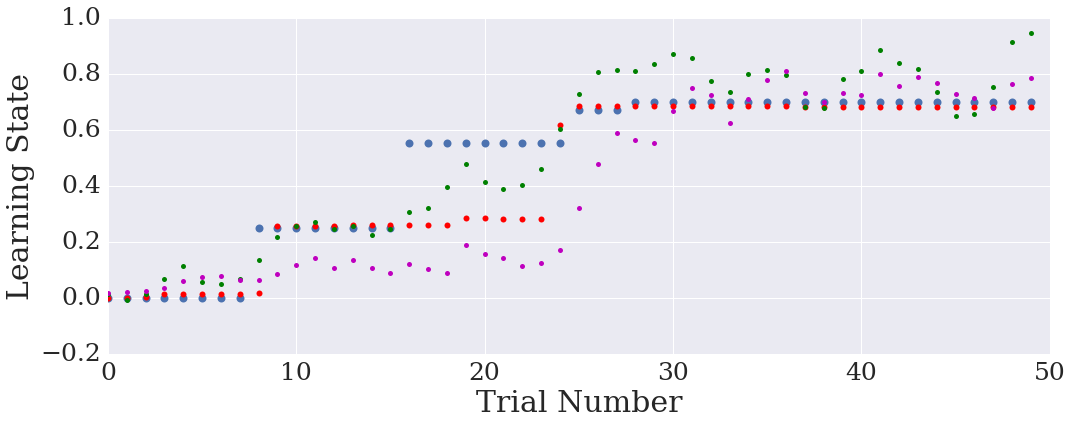
plt.figure(figsize=(15,6)) ns = range(N) plt.plot(ns,X,'o',label=r'True Learning State',markersize=8) plt.plot(ns,x_admm,'ro',label=r'ADMM Estimate',markersize=6) plt.plot(ns,x_kalman,'go',label=r'FIS Estimate',markersize=5) plt.plot(ns,x_particle,'mo',label=r'SMC Estimate',markersize=5) plt.xlabel(r'Trial Number',fontsize=30) plt.ylabel(r'Learning State',fontsize=30) plt.tick_params(axis='both', which='major', labelsize=25) plt.tight_layout() if save_figs: plt.savefig(fig_dir + 'ssml_gauss_state.eps', format='eps', dpi=1000) plt.show()
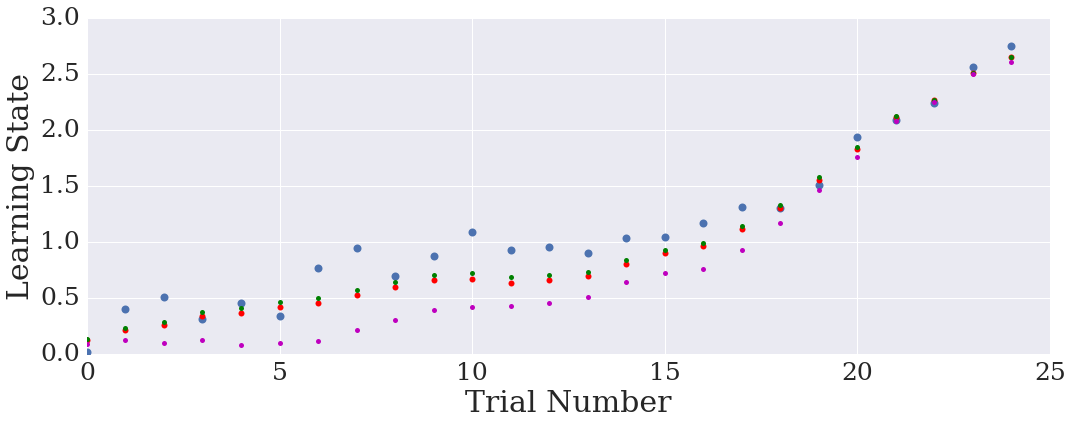
plt.figure(figsize=(15,6))
ns = range(N)
plt.plot(ns,X,'o',label='True Learning State',markersize=8)
plt.plot(ns,x_admm,'ro',label='ADMM Estimate',markersize=6)
plt.plot(ns,x_kalman,'go',label='FIS Estimate',markersize=5)
plt.plot(ns,x_particle,'mo',label='SMC Estimate',markersize=5)
plt.xlabel('Trial Number',fontsize=30)
plt.ylabel('Learning State',fontsize=30);
plt.tick_params(axis='both', which='major', labelsize=25)
plt.tight_layout()
if save_figs: plt.savefig(fig_dir + 'ssml_sparse_variations.eps', format='eps', dpi=1000)
plt.show()
T = 5
Del = 0.001
J = int(T/Del)
psi = -3.5
g = 2.0
c = [-20,-5,1,3]
R = np.zeros((N,J))
for n in range(N):
for j in range(J):
c_sum = 0
for s in range(len(c)):
if(j-(s+1)>=0):
c_sum += c[s]*R[n,j-(s+1)]
lam_nj = np.exp(psi + g*X[n] + c_sum)
R[n,j] = bern.rvs(lam_nj*Del*np.exp(-lam_nj*Del),size=1)
R_vec = R.reshape(N*J,1)
plt.figure(figsize=(15,4))
plt.plot(np.arange(0,N*J/1000,1/1000),R_vec,linewidth=0.3)
plt.xlim([0,N*J/1000])
plt.xticks(range(0,130,5))
plt.xlabel('Time (s)')
plt.ylabel('Spiking Activity')
plt.tight_layout();

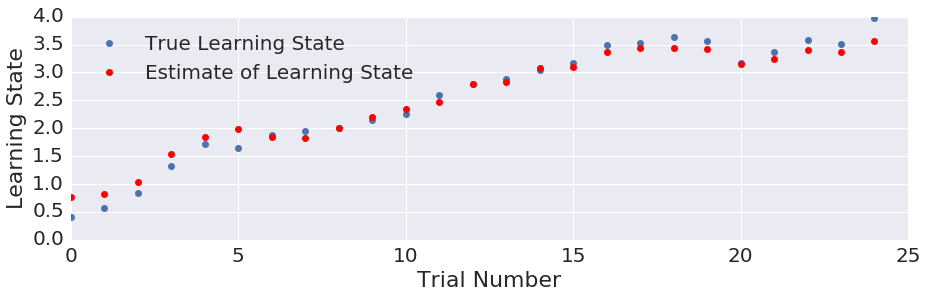
plt.figure(figsize=(15,4))
ns = range(N)
plt.plot(ns,X,'o',label='True Learning State')
plt.plot(ns,x,'ro',label='Estimate of Learning State')
plt.legend(loc=2)
plt.xlabel('Trial Number')
plt.ylabel('Learning State');
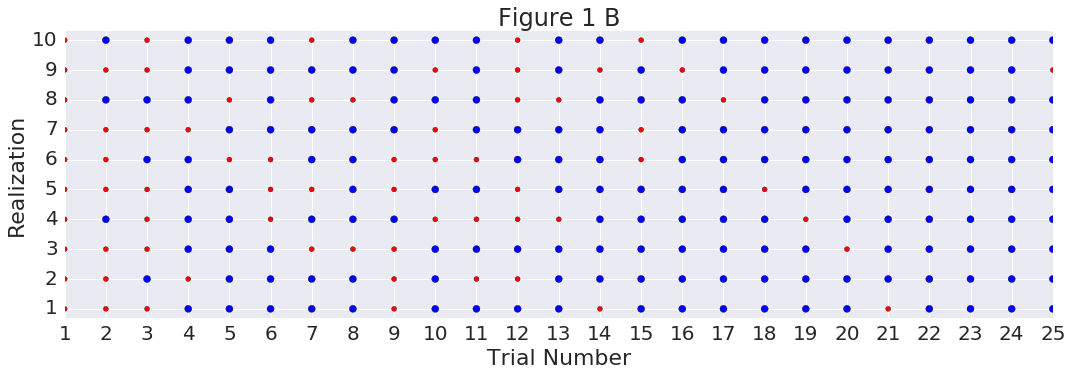
plt.scatter(range(1,N+1),[event+1]*N,c=col,s=s)
plt.xlim(1,N)
plt.xticks(range(1,N+1))
plt.ylim([1-.3,num+0.3])
plt.xlabel('Trial Number')
plt.ylabel('Realization')
plt.yticks(range(1,num+1))
plt.tight_layout();
plt.title("Figure 1 B");
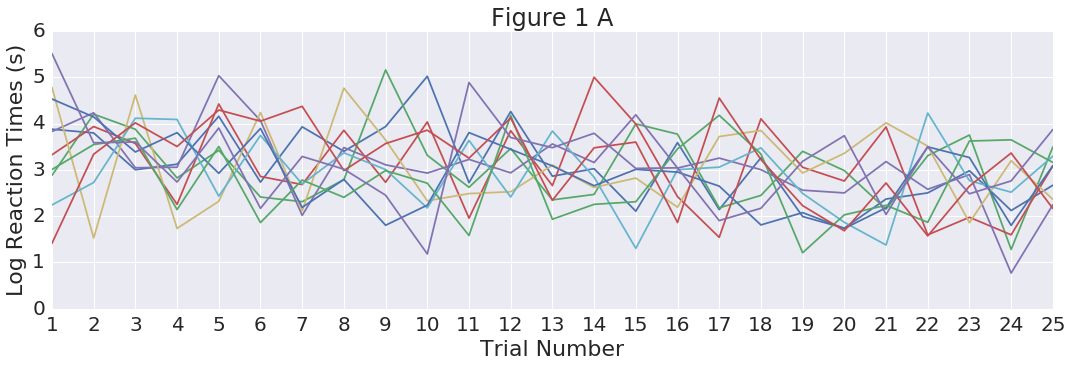
# Plot neural spiking
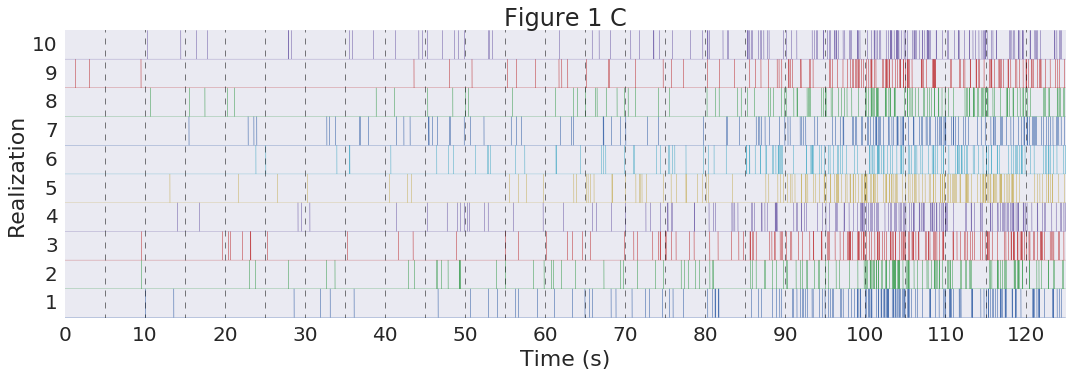
plt.figure(figsize=(15,5))
for event in range(num):
R_vec = Rs[event,:,:].reshape(N*J,1)
plt.plot(np.arange(0,N*J/1000,1/1000),R_vec+event+0.5,linewidth=0.3)
for n in range(N-1):
plt.plot([(n+1)*T,(n+1)*T],[0,num+2],'k--',linewidth=0.5)
plt.xlim([0,N*J/1000])
plt.ylim([1-.51,num+.5])
plt.xticks(range(0,130,10))
plt.xlabel('Time (s)')
plt.ylabel('Realization')
plt.yticks(range(1,num+1))
plt.grid('off')
plt.tight_layout();
plt.title("Figure 1 C");
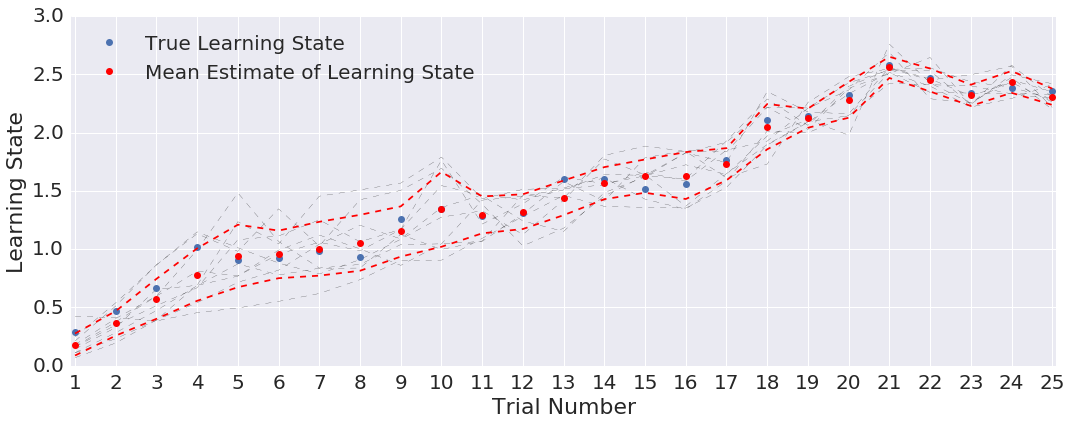
plt.figure(figsize=(15,6))
ns = range(1,N+1)
for event in range(num):
plt.plot(ns,xs[event,:],'k--',linewidth=0.2)
plt.plot(ns,X,'o',label='True Learning State')
plt.plot(ns,np.mean(xs,axis=0),'ro',label='Mean Estimate of Learning State')
plt.plot(ns,np.mean(xs,axis=0)-np.std(xs,axis=0),'r--')
plt.plot(ns,np.mean(xs,axis=0)+np.std(xs,axis=0),'r--')
plt.legend(loc=2)
plt.xticks(range(1,N+1))
plt.xlim([0.9,N+0.1])
plt.xlabel('Trial Number')
plt.ylabel('Learning State')
plt.tight_layout();
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
Gabriel Schamberg, Demba Ba, Todd P. Coleman (2018)




















 784
784

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








