利用BP神经网络进行公路客运货运量的预测

    公路运量主要包括公路客运量和公路货运量两个方面。据研究，某地区的公路运量主要与该地区的人数、机动车数量和公路面积有关，表中给出了某地区20年的公路运量相关数据。

    根据相关部门数据，该地区2021年和2022年的人数分别为73.39万和75.55万人，机动车数量分别为3.9635万和4.0975万辆，公路面积将分别为0.9880万和1.0268万平方千米。请对该地区2021年和2022年的公路客运量和公路货运量进行预测。

年份	人口数量/万人	机动车数量/万辆	公路面积/万平方千米	公路客运量/万人	公路货运量/万吨
2001	20.55	0.6	0.09	5126	1237
2002	22.44	0.75	0.11	6217	1379
2003	25.37	0.85	0.11	7730	1385
2004	27.13	0.9	0.14	9145	1399
2005	29.45	1.05	0.2	10460	1663
2006	30.1	1.35	0.23	11387	1714
2007	30.96	1.45	0.23	12353	1834
2008	34.06	1.6	0.32	15750	4322
2009	36.42	1.7	0.32	18304	8132
2010	38.09	1.85	0.34	19386	8936
2011	39.13	2.15	0.36	21024	11099
2012	39.99	2.2	0.36	19490	11203
2013	41.93	2.25	0.38	20433	10524
2014	44.59	2.35	0.49	22598	11115
2015	47.3	2.5	0.56	25107	13320
2016	52.89	2.6	0.59	33442	16762
2017	55.73	2.7	0.59	36836	18637
2018	56.76	2.85	0.67	40548	20724
2019	59.17	2.95	0.69	42927	20803
2020	60.63	3.1	0.79	43462	21804

代码如下

rs=xlsread('C:\Users\86135\Desktop\matlab\back propagation','B2:B21')
jdcs=xlsread('C:\Users\86135\Desktop\matlab\back propagation','C2:C21')
glmj=xlsread('C:\Users\86135\Desktop\matlab\back propagation','D2:D21')
glkyl=xlsread('C:\Users\86135\Desktopmatlab\\back propagation','E2:E21')
glhyl=xlsread('C:\Users\86135\Desktop\matlab\back propagation','F2:F21')
p=[rs';jdcs';glmj']    %输入数据矩阵
t=[glkyl';glhyl']    %目标数据矩阵
[pn,minp,maxp,tn,mint,maxt]=premnmx(p,t)    %利用premnmx函数对数据归一化
dx=[-1,1;-1,1;-1,1]    %归一化处理后最小值为-1，最大值为1
net=newff(dx,[3,7,2],{'tansig','tansig','purelin'},'traingdx')    %建立模型，并用梯度下降法训练
net.trainParam.show=1000    %1000轮回显示一次结果
net.trainParam.Lr=0.05    %学习速度为0.05
net.trainParam.epochs=50000    %最大训练轮回为50000次
net.trainParam.goal=0.65*10^(-3)    %均方误差
net=train(net,pn,tn)    %开始训练，其中pn,tn分别为输入输出样本
an=sim(net,pn)    %用训练好的模型进行仿真
a=postmnmx(an,mint,maxt)    %把仿真得到的数据还原为原始的数量级
x=2001:2020
newk=a(1,:)
newh=a(2,:)
figure(2)
subplot(2,1,1)    %绘制公路客运量对比图
plot(x,newk,'r-o',x,glkyl,'b--+')
legend('网络输出客运量','实际客运量')
xlabel('年份')
subplot(2,1,2)    %绘制公路货运量对比图
plot(x,newh,'r-o',x,glhyl,'b--+')
legend('网络输出货运量','实际货运量')
xlabel('年份')
ylabel('货运量/万吨')
pnew=[73.59,75.55;3.9635,4.0975;0.9880,1.0268]
pnewn=tramnmx(pnew,minp,maxp)    %利用原始输入数据的归一化参数对新数据进行归一化
anewn=sim(net,pnewn)    %利用归一化后的数据进行仿真
anew=postmnmx(anewn,mint,maxt)    %把仿真得到的数据还原为原始的数量级

运行结果如图

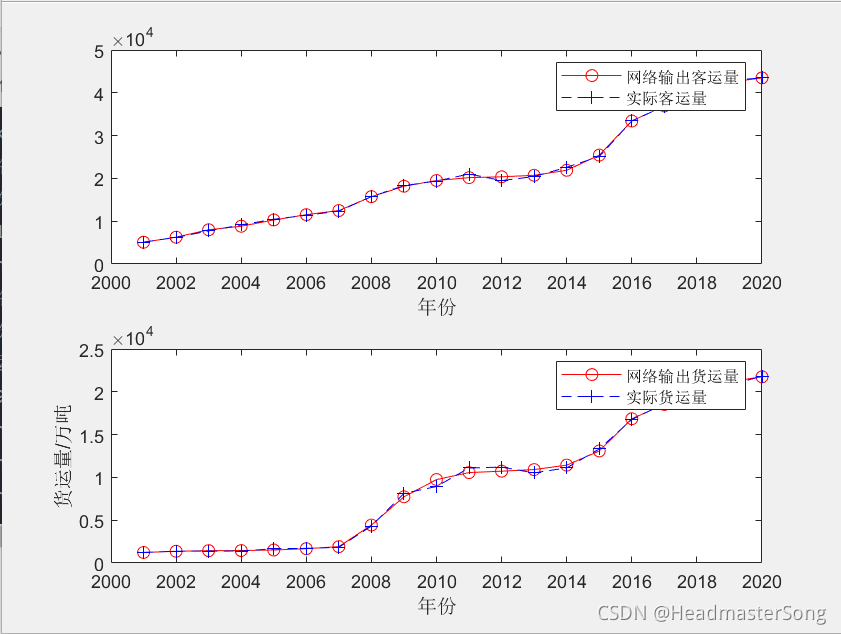
 可以得到anew的值为[43790,43785;21704,21705]。也就是说，2021年和2022年的公路客运量分别达到43790万人和43785万人，公路货运量分别为21704万吨和21705万吨。由于样本数量较少，再次运行时得到的结果可能会有不同。

材料来源：中法核威斯布鲁柯