Oja’s rule

Oja’s rule

这俩天看了Oja的俩篇论文，被其中的证明弄得云里雾里，但愿我的理解没有出太大问题吧。
Oja’s rule Wiki
Oja’s rule 知乎

• A Simplified Neuron Model as a Principal Component Analyzer
• On Stochastic Approximation of Eigenvectors and Eigenvalues of the Expectation of a Random Matrix

背景

貌似是关于神经网络，权重的无监督训练的。有趣的是，由这个出发点，可以得到一种关于stream PCA的算法，即Oja’s rule。

Hebbian learning

在Hebb的假说中，对于权重的调整为：
$△w_i=\eta x_{i}y$
where:
$y=\sum _j{w}_j{x}_j$

在stream PCA表述为这样的算法:
${\tilde{X}}_k=X_{k-1}+A_k{X}_{k-1}{\Gamma }_k$
$X_k={\tilde{X}}_k{R}_k^{-1}$
where:
$X_k$就是每一次迭代所得的正交矩阵，$A_k$为随机矩阵，在stream PCA里面，一般$A_k=z_k{z}_k^{\top }\in {\mathbb{R}}^{d\times d}$， ${\Gamma }_k$是一个对角矩阵，每个对角元素表示对应列向量的学习率。$R_k^{-1}$怎么说呢，$X_k=QR$这个$QR$分解，$R_k^{-1}$就是$R$的逆。
当只需要最大特征值所对应的特征向量的时候:
${\tilde{x}}_k=x_{k-1}+{\gamma }_k{A}_k{x}_{k-1}$
$x_k={\tilde{x}}_k/\Vert {\tilde{x}}_k\Vert$

这个式子到底啥含义呢，为什么会这样呢？
Oja给出的分析是（大概是这样）：
$x_k$关于${\gamma }_k$的泰勒展式(只到一次项)是：
$x_k=x_{k-1}+{\gamma }_k[A_k{x}_{k-1}-(x_{k-1}^{\top }{A}_k{x}_{k-1})x_{k-1}]+{\gamma }_k{b}_k$
where:
$b_k=o({\gamma }_k)$这个地方我有个疑问，不知道是我对论文的理解不对还是如何，我觉得如果$b_k=o({\gamma }_k)$，那么前面就不必再乘上个${\gamma }_k$了。
还要注意的一点是，上面的推导用到了:$\Vert x_{k-1}\Vert =1$的条件。
上面的式子还可以有另外一种写法:
$x_k=x_{k-1}+{\gamma }_k[A{x}_{k-1}-\frac{(x_{k-1}^{\top }A{x}_{k-1})}{x_{k-1}^{\top }{x}_{k-1}}{x}_{k-1}]+{\gamma }_k[(A_k-A)x_{k-1}-(x_{k-1}^{\top }(A_k-A)x_{k-1})x_{k-1}]+{\gamma }_k{b}_k$
这个式子只是对上面的加项减项处理，并不难推导。注意，请想象$E(A_k)=A$
保留右边前俩项:
$△x_k\approx {\gamma }_k[A{x}_{k-1}-\frac{(x_{k-1}^{\top }A{x}_{k-1})}{x_{k-1}^{\top }{x}_{k-1}}{x}_{k-1}]$

连续情况下就可以得到形如下面的微分方程:
$\frac{dz}{dt}=Az-\frac{(z^{\top }Az)}{z^{\top }z}z$
微分方程的内容我忘得差不多了，这个方程的解法大概是这样的:
$z:=\sum _i{\eta }^{(i)}(t)c_i$
where:
$c_i$是矩阵$A$的按特征值由大到小排列的单位特征向量。
这时，上面的微分方程可以分解为$d$（论文里纬度是$n$）个子微分方程：
$\frac{d{\eta }^{(i)}}{dt}={\lambda }^{(i)}{\eta }^{(i)}-\frac{(z^{\top }Az)}{z^{\top }z}{\eta }^{(i)}$
令：${\zeta }^{(i)}={\eta }^{(i)}/{\eta }^{(1)}$ (${\eta }^{(1)}(t)̸=0$),容易推得（是真的不是假的）:
$\frac{d{\zeta }^{(i)}}{dt}=({\lambda }^{(i)}-{\lambda }^{(1)}){\zeta }^{(i)}$

可以推得其解为:
${\zeta }^{(i)}(t)=exp[({\lambda }^{(i)}-{\lambda }^{(1)})t]{\zeta }^{(i)}(0)$
从这个式子可以看到，只要${\eta }^{(1)}(t)̸=0$，那么其他成分，随着时间的增长，会趋于0，所以最后$z$会成为$c_1$。
上面的算法的内涵就是其线性主部满足这个性质。上面微分方程还有另外一个性质:
$\Vert z(0)\Vert =1$则$\Vert z(t)\Vert =1,t>0$(通过求导，导数为0可以验证！)
这也就是说，我们只要保证第一次，后面的大小也可以同样保证。当然，这些条件是在连续情况下推导的，实际在离散的情况下，我们要求${\gamma }_k$足够小。

主要的一些理论

论文里面一些主要的假设

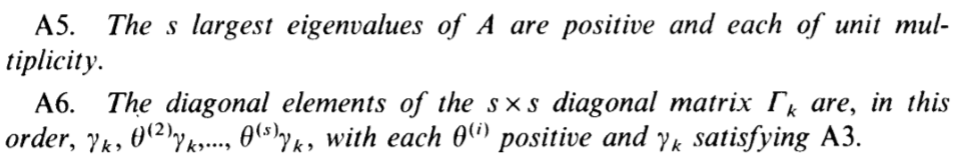
我不怎么理解的地方是这个unit multiplicity，是特征值是唯一的吗(从证明中看似乎是这样的)？

引理1

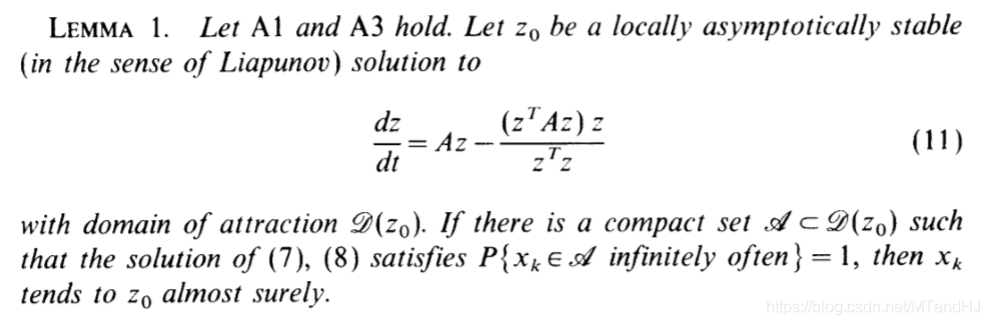
引理2

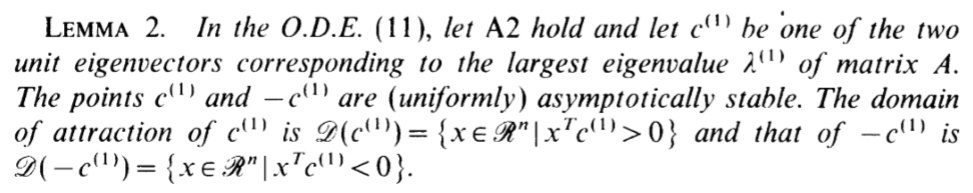
引理3

(7) (8)就是上面的$x_k$的迭代算法:
${\tilde{x}}_k=x_{k-1}+{\gamma }_k{A}_k{x}_{k-1}$
$x_k={\tilde{x}}_k/\Vert {\tilde{x}}_k\Vert$

定理1

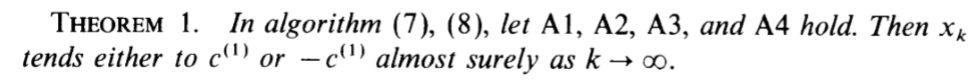
下面Oja开始讨论$X_k$的迭代算法:

LEMMA 3（ALL）

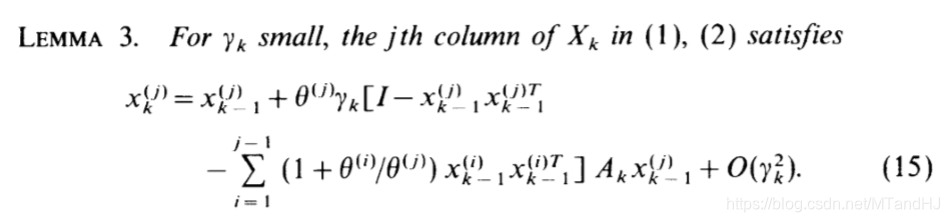
（1）（2）是关于$X_k$的迭代算法。

引理 4

定理 2

定理 3（关于特征值）

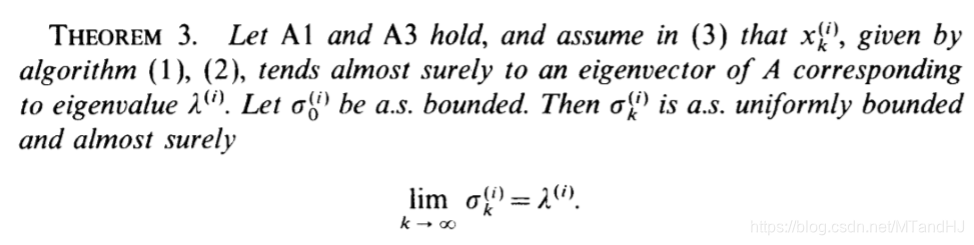
关于$\sigma$的迭代算法，即（3）：
${\sigma }_k^{(i)}=(1-{\gamma }_k){\sigma }_{k-1}^{(i)}+{\gamma }_k(x_{k-1}^{(i)}{A}_k{x}_{k-1}^{(i)})$

Oja’s rule

Oja’s rule 是对 Hebbian learning 的改进:

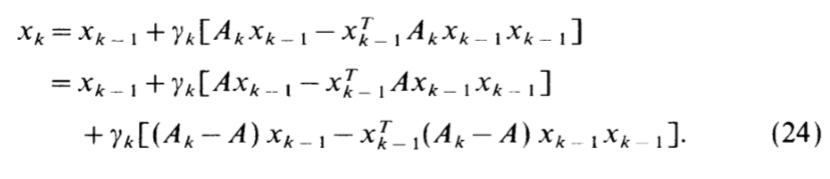
可以发现，其实Oja’s rule就是取了前面的线性主部。
相应的微分方程变为:
$\frac{dz}{dt}=Az-(z^{\top }Az)z$
性质有所欠缺，但是，在一定条件下依然可以保证一些良性。

引理 5（关于${\gamma }_k$的选择）

定理 3

注意，当推广到求解$X_k$的时候有俩种:

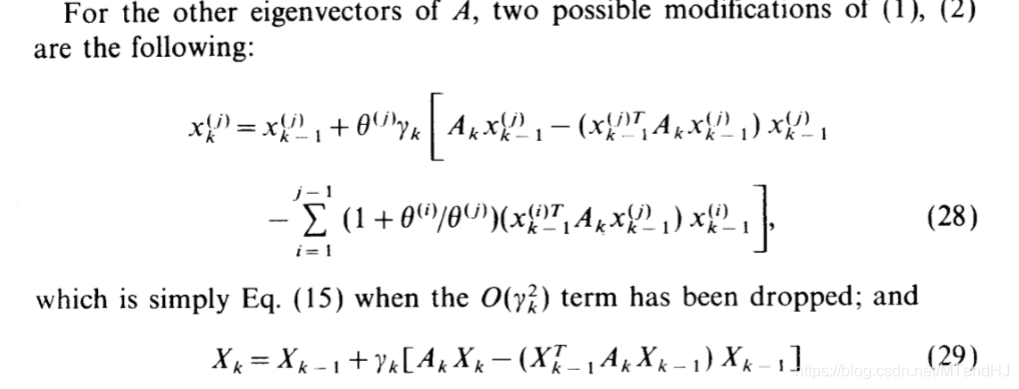
(29)的列不一定是相应的特征向量，但列所构成的子空间是一致的！

数值实验

我们先用均匀分布产生一个基础向量x，再在其上添加由标准正态分布所生成噪声，得到一串向量，来模拟数据。

dfv1: Hebbian方法得到的向量与特征向量的cos值
dfv2: Oja方法得到的向量与特征向量的cos值
dfx1: Hebbian方法得到的向量与x的cos值
dfx2: Oja方法得到的向量与x的cos值
dfAx: x与特征向量的cos值

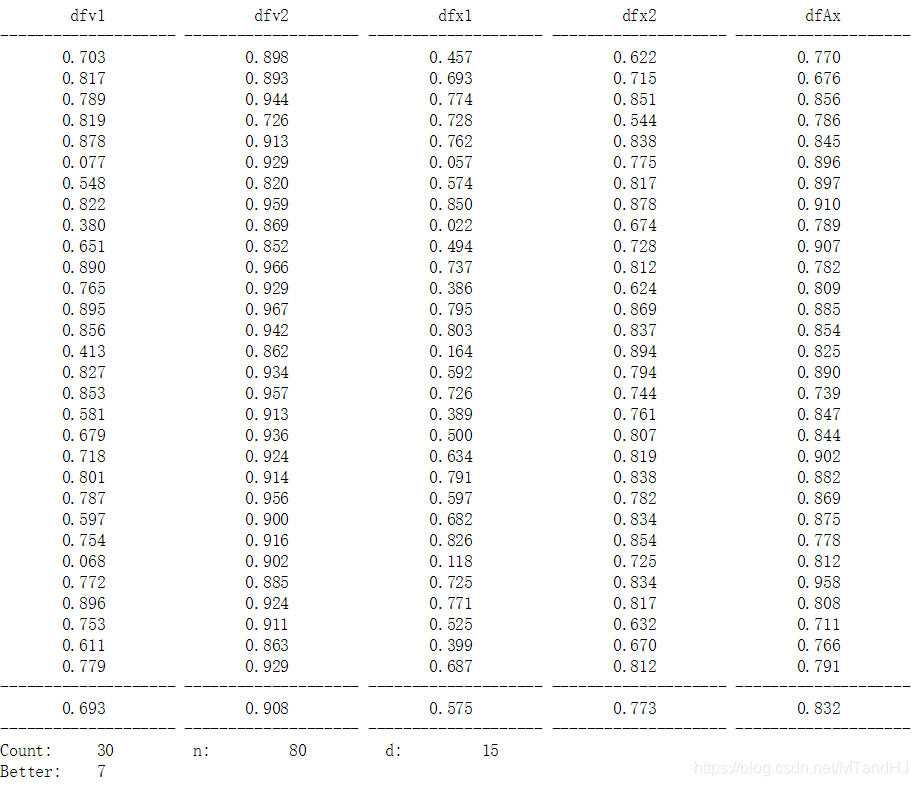
用Oja’s rule 大概80次就能到达0.90的水准，与x的差距也不大，有7次比特征向量还要好！而Hebbian learning 大概300次。当然，这可能与我对步长的调整有关系，但是说实话，我已经尽力了。

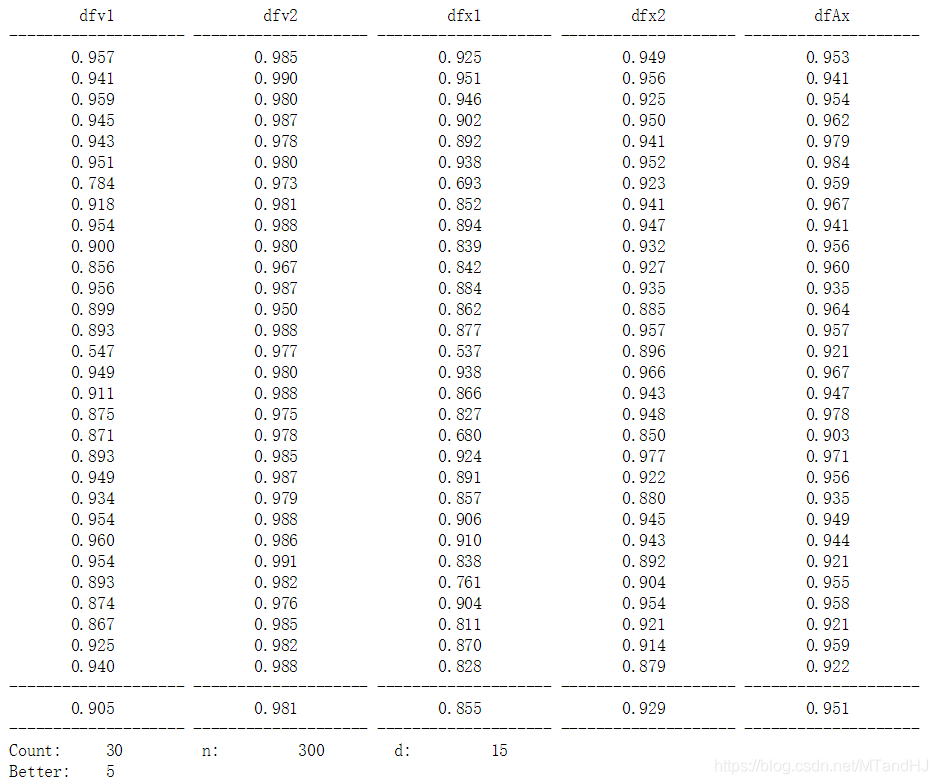
代码

import numpy as np
def Oja_rule_1(x_old, z, r):  #实际上好像不是Oja's  修正Hebbian learning
    
    x = x_old + r * np.dot(x_old, z.T.dot(z))
    x = x / np.sqrt(x @ x)
    
    return x

def Oja_rule_2(x_old, z, r):
    
    x = x_old + r * (x_old @ (z.T @ z) - x_old @ (z.T @ z) @ x_old * x_old)
    
    return x
def D2D(x, y): #计算cos值，Oja的论文用的是2范数
    
    return abs(x @ y)

def Main(d, n):
    
    x = np.array([np.random.rand() for i in range(d)])
    x = x / np.sqrt(x @ x)
    A = np.array([ x + [np.random.randn() for j in range(d)] for i in range(n)])
   #以上是生成数据
    A_vector = np.linalg.eig(A.T.dot(A))[1][:,0] #数据的主特征向量
    x_new_1 = np.array([np.random.rand() for i in range(d)])
    #print(x_new_1)
    x_new_1 = x_new_1 / np.sqrt(x_new_1 @ x_new_1)
    x_new_2 = x_new_1
    for i in range(n):
        z = A[i,:]
        r1 = np.log(i + 2) / (i + 1) # 按照论文的理解，是不需要加乘上log部分的，可是不加log部分的效果也忒差了
        r2 = 2 / max((3 * z @ z), i + 1)
        z.resize(1,len(z))
        x_new_1 = Oja_rule_1(x_new_1, z, r1)
        x_new_2 = Oja_rule_2(x_new_2, z, r2)
    
    x_new_2 = x_new_2 / np.sqrt(x_new_2 @ x_new_2)
    
    dfv1 = D2D(A_vector, x_new_1)
    dfv2 = D2D(A_vector, x_new_2)
    dfx1 = D2D(x, x_new_1)
    dfx2 = D2D(x, x_new_2)
    dfAx = D2D(A_vector, x)
    
    return dfv1, dfv2, dfx1, dfx2, dfAx

def Summary(times, d, n):
    
    print('{0:^20} {1:^20} {2:^20} {3:^20} {4:^20}'.format('dfv1', 'dfv2', 'dfx1', 'dfx2', 'dfAx'))
    print('{0:-<20} {0:-<20} {0:-<20} {0:-<20} {0:-<20}'.format(''))
    M = np.array([0.] * 5)
    Better = 0
    for time in range(times):
        
        result = Main(d, n)
        M += result
        if result[-2] > result[-1]:
            Better += 1
        print('{0[0]:^20.3f} {0[1]:^20.3f} {0[2]:^20.3f} {0[3]:^20.3f} {0[4]:^20.3f}'.format(result))
        
    print('{0:-<20} {0:-<20} {0:-<20} {0:-<20} {0:-<20}'.format(''))
    print('{0[0]:^20.3f} {0[1]:^20.3f} {0[2]:^20.3f} {0[3]:^20.3f} {0[4]:^20.3f}'.format(M / times))
    
    print('{0:-<20} {0:-<20} {0:-<20} {0:-<20} {0:-<20}'.format(''))
    print('{0:<10} {1:<10} {2:<10} {3:<10} {4:<10} {5:<10}'.format('Count:', times, 'n:', n, 'd:', d))
    print('{0:<10} {1:<20}'.format('Better:', Better))

Summary(30, 15, 300)