3 概率分布与随机函数

更多MATLAB数据分析视频请点击，或者在网易云课堂上搜索《MATLAB数据分析与统计》 http://study.163.com/course/courseMain.htm?courseId=1003615016

 

  随着计算机技术的快速发展，随机数在越来越多的领域得到了广泛应用，例如信息安全，网络游戏，计算机仿真和模拟计算，这一章将介绍常用的概率分布及概率计算、利用MATLAB生成随机数。

 1.概率分布及概率计算

   1.1 概率分布的定义

   设X为一随机变量，对任意实数x，定义

         F（x）=P（X<=x）

   为X的分布函数。根据随机变量取值的特定，随机变量分为离散型和连续型两种。P为X的概率函数

 1.2 几种常见的概率分布

   （1）二项分布

       若随机变量X的概率函数为

 

则称X服从二项分布，记为X~B（n，p）。其期望E（X）=np，方差var（X）=np（1-p）。

 （2）泊松分布

   若随机变量X的概率函数为

 

  则称X服从参数为λ的泊松分布，记为X~P（λ）。其期望E（x）=λ，方差var（X）=λ。

（3）离散均匀分布

 若随机变量X的概率函数为

 

   则称X服从离散的均匀分布

 （4）连续均匀分布

  若随机变量X的概率密度函数为

 

则称X服从区间[a,b]上的连续均匀分布，记为X~U（a，b）。其期望E（X）=（a+b）/2，方差var(X)=(b-a)^2/12.

（5）指数分布

若随机变量X的概率密度函数为

其中λ>0为参数，则称X服从指数分布，记为X~Exp（λ）。其期望E（X）=λ，方差var（x）=λ^2

（6）正态分布

  若随机变量X的概率密度函数为

 

其中，σ>0,μ为分布参数，则称X服从正态分布，记为X~N（μ，σ^2）,其期望E（X）=μ，方差var（X）=σ^2。特别地，当μ=0，σ=1时，称X服从标准正态分布，记为X~N（0,1）。

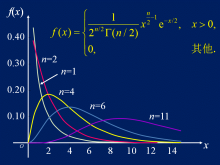
（7）卡方分布

若n个相互独立的随机变量ξ₁、ξ₂、……、ξn ，均服从标准 正态分布（也称独立同分布于 标准正态分布），则这n个服从标准正态分布的随机变量的平方和

构成一新的随机变量，其