本文介绍了如何使用动态规划解决一个关于构建以1到n整数为节点的二叉搜索树的问题，通过递推公式dp[i]=dp[j-1]*dp[i-j]计算不同节点数的二叉搜索树数量。同时提及了与01背包问题的相似性，利用滚动数组优化空间复杂度。
96.不同的二叉搜索树
给定一个整数 n，求以 1 ... n 为节点组成的二叉搜索树有多少种？
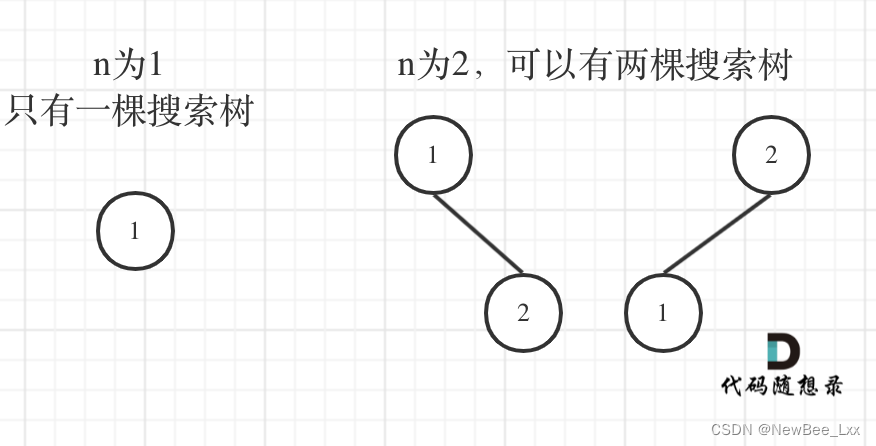
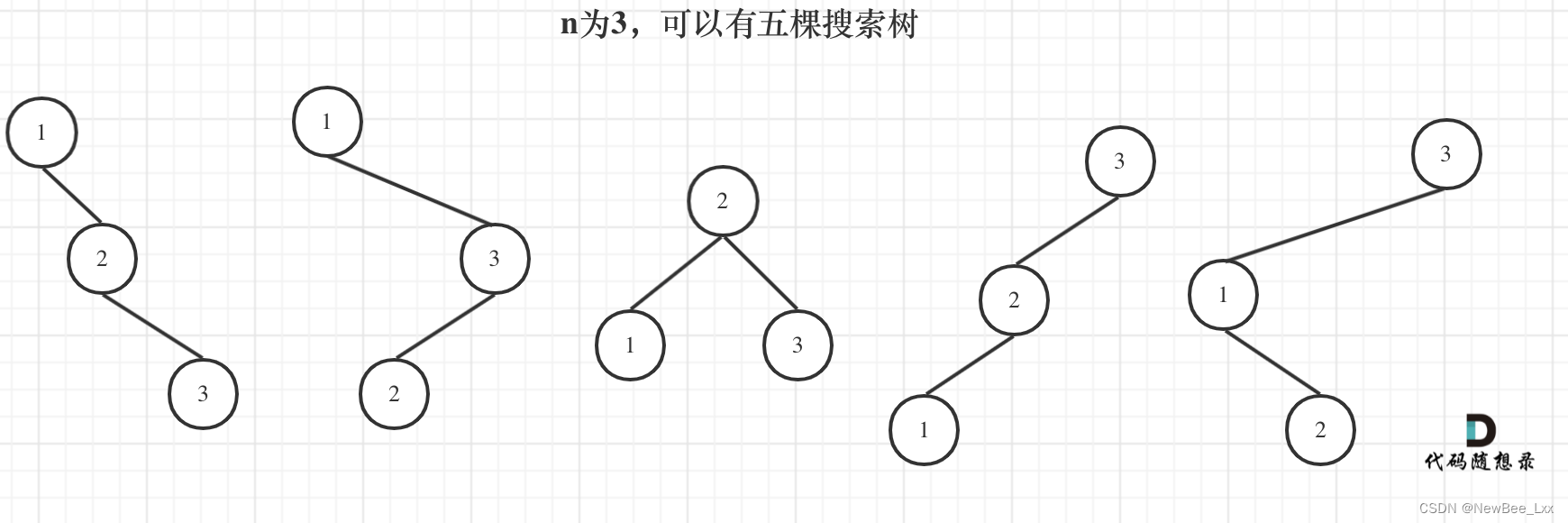
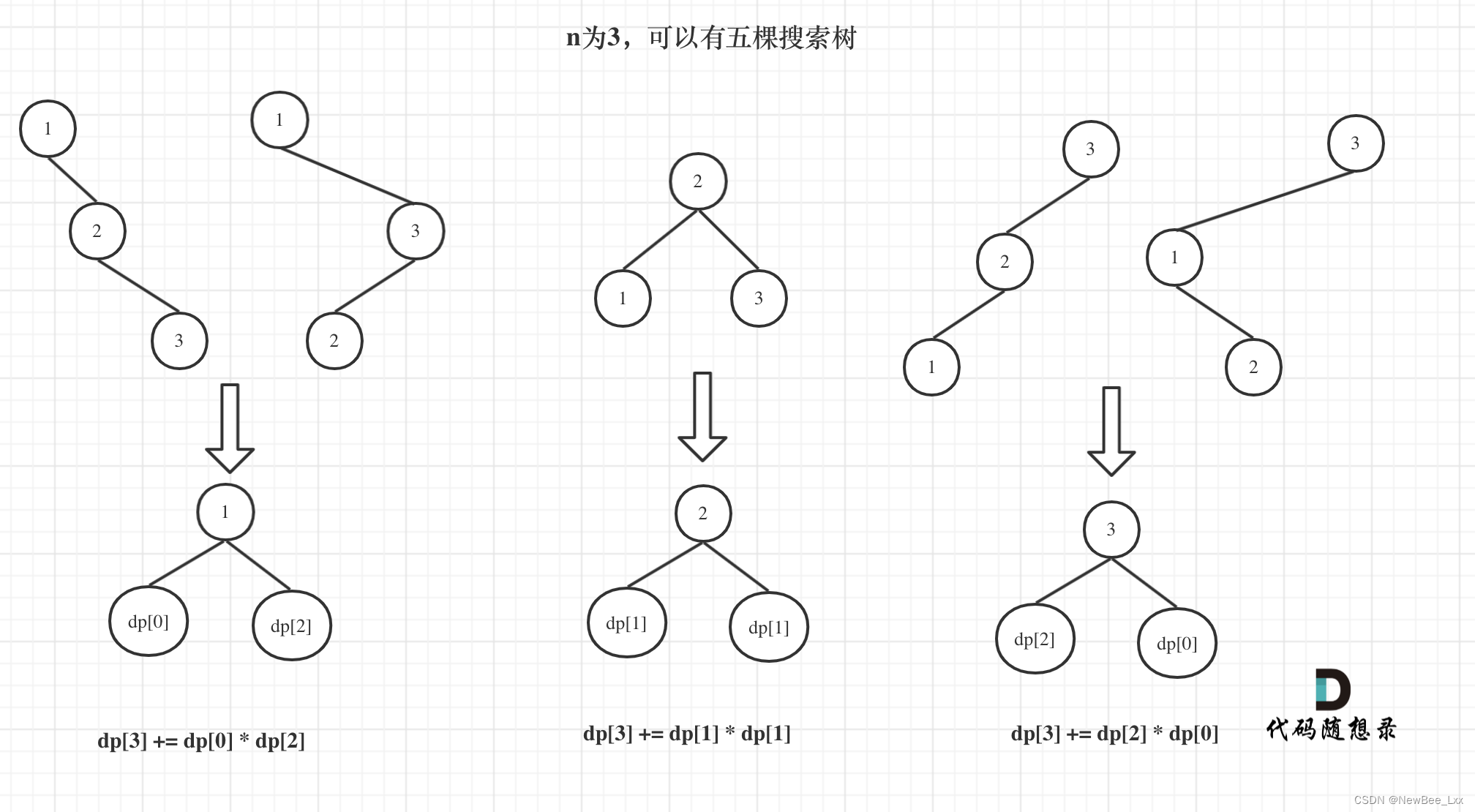
dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]
dp[i] ： 1到i为节点组成的二叉搜索树的个数为dp[i]。
dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]
j相当于是头结点的元素，从1遍历到i为止。
所以递推公式：dp[i] += dp[j - 1] * dp[i - j]; ，j-1 为j为头结点左子树节点数量，i-j 为以j为头结点右子树节点数量
空节点也是一棵二叉树,所以初始化dp[0] =
最低0.47元/天 解锁文章
扫一扫
1885
到【灌水乐园】发言
