LeetCode 110. 平衡二叉树

最新推荐文章于 2025-09-03 23:48:37 发布

原创最新推荐文章于 2025-09-03 23:48:37 发布 · 401 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构

LeetCode 专栏收录该内容

40 篇文章

订阅专栏

本文探讨了两种判断二叉树是否平衡的有效方法。首先介绍了通过前序遍历计算二叉树高度，但存在大量重复计算的问题。随后，提出了利用后序遍历并记录高度的优化方案，有效避免了重复计算，提高了判断效率。

题目：判断一棵二叉树是否为平衡二叉树。所谓的平衡二叉树是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

容易被大家忽视的一点：平衡二叉树（AVL）一定是一棵二叉搜索树（BST）

思路一：按照前序遍历判断

（1）判断以根结点的树是否为二叉平衡树,求出左右子树的高度,判断它们的高度差的绝对值是否大于1;
（2）递归判断根的左子树是否为平衡二叉树;
（3）递归判断根的右子树是否为平衡二叉树;
（4）空树也是平衡二叉树。

下面给出求二叉树高度的代码和递归的判断是否为平衡二叉树的代码

//求二叉树的高度
int BinaryTreeHigh(BiTree* root)
{
    if (root == NULL)
    {
        return 0;
    }
    int left = BinaryTreeHigh(root->left);  //递归的求左子树的高度;
    int right = BinaryTreeHigh(root->right); //递归的求右子树的高度;
    //二叉树的高度为左子树和右子树的高度最大值再加1
    return left > right ? left + 1 : right + 1;
}

//判断树是否为平衡二叉树
bool IsBalancedTree(BiTree* root)
{
    //空树是平衡二叉树;
    if (root == NULL)
    {
    	 return true;
	}  
    int left = BinaryTreeHigh(root->left); 	 //左子树深度;
    int right = BinaryTreeHigh(root->right); //右子树深度;
    int height = right - left;  //求高度差;
    if (height > 1 || height < -1)     //深度超过1则不是平衡二叉树,返回false;
    {
    	return false;
    }
    //递归判断子树
    return IsBalancedTree(root->left) && IsBalancedTree(root->right);
}

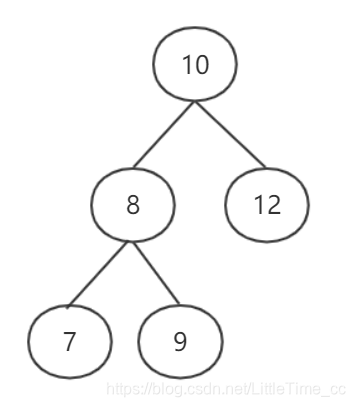
对于思路1的代码,存在着大量的重复计算,我们借助下图来举例说明存在的问题,从10开始求深度时，要遍历8和7,再判断以8为根的树是否为平衡二叉树时还要遍历7和9。所以这种方法存在着大量重复的计算,为了改进这个这个缺点,我们引入下面的思路二。

在这里插入图片描述

思路二：按照后序遍历判断(记录高度,避免重复求高度)

（1）判断左子树是否为平衡二叉树;
（2）判断右子树是否为平衡二叉树;
（3）判断是否为平衡二叉树的同时,记录它们的左右子树的高度;
（4）最后再判断以这个结点为根的树是否为平衡二叉树。

//判断树是否为平衡二叉树;
bool IsBalancedTree(BiTree* root, int &depth)
{
    if (root == NULL)
    {
        depth = 0;
        return true;
    }
    //按照后序遍历的规则去判断,先判断左、右子树，然后记录以当前结点为根的树的高度;
    int left, right;
    if (IsBalancedTree(root->left, left) && IsBalancedTree(root->right, right))
    {
        int height = right - left;
        if (height <= 1 && height >= -1)
        {
            depth = left>right ? left + 1 : right + 1;
            return true;
        }
    }
    return false;
}