221.最大正方形

解题思路：

暴力法+优化

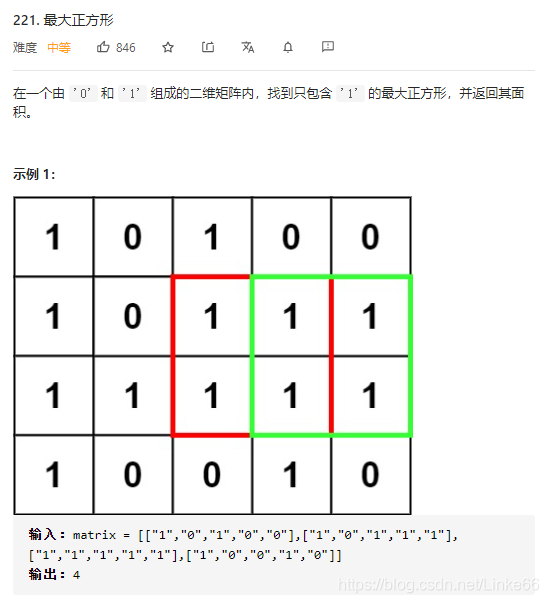
offset是指从当前格，边长为1，向右向下偏移offset格，比如offset=2，那么就形成一个边长为1+2=3的正方形。

设置一个辅助函数，根据当前格的坐标（x，y）和offset，来判断这是否是一个有效的正方形。

1 假如x+offset或者y+offset越界，无效正方形，返回假；
2 假如没有越界，但是内部有字符‘0’，也是无效正方形，返回假；
3 否则返回真。

好了，有了这个辅助函数，我们只需要遍历matrix每个元素，并且尝试每种offset，记录最大的offset就可以了。

优化：
1 max_offset用来记录当前最大的偏移量，那么在第三重循环中，就不用考虑小于max_offset的情况了；
2 假如offset=1的时候就是无效正方形，那么大于offset的情况也不用考虑了。

注意：
最后的正方形边长是res+offset，res=1；
假如存在元素全为0的matrix，那么最终边长就是0，res=0。

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        int m=matrix.size();
        int n=matrix[0].size();
        //最大的size是最短边-1
        int size=min(m-1,n-1);

        int res=0;
        int max_offset=0;   //记录目前最大偏移量
        for(int x=0;x<m;++x){    //遍历每一个位置
            for(int y=0;y<n;++y){
                for(int offset=max_offset;offset<=size;++offset){ //offset从当前所能最大的偏移开始
                    if(isValidSquare(matrix,x,y,offset)){ //判断是否是一个有效的正方形
                        if(offset>max_offset)  //假如有效的offset大于max_offset
                            max_offset=offset; //更新max_offset
                            res=1;
                    }else{
                        break;  //否则直接结束本次for循环
                    }
                }
            }
        }
        res+=max_offset;
        res*=res;
        return res;
    }

    bool isValidSquare(vector<vector<char>>&matrix,int x,int y,int offset){
        int m=matrix.size();
        int n=matrix[0].size();
        if((x+offset>=m)||(y+offset>=n)) return false;
        if((x+offset)<m&&(y+offset)<n){
            for(int i=x;i<=x+offset;++i){
                for(int j=y;j<=y+offset;++j){
                    if(matrix[i][j]=='0')return false;
                }
            }
        }
        return true;
    }
};