学习吴恩达课程笔记
决策树 decision tree
建立决策树之前的工作
- 选定决策节点
- 选择能使划分浓度高的特征作为决策节点
- 决定停止
- 一个节点100%是一个类(熵为0)
- 选择树的最大深度
- 纯度得分(新划分的信息增益小于某个阈值)
- 一个节点的示例数量低于某个阈值 (比如当前节点小于9个样本,就不再分了)
检验不纯度指标:熵
例如识别猫的样例,p1是猫在所有样例中的比例
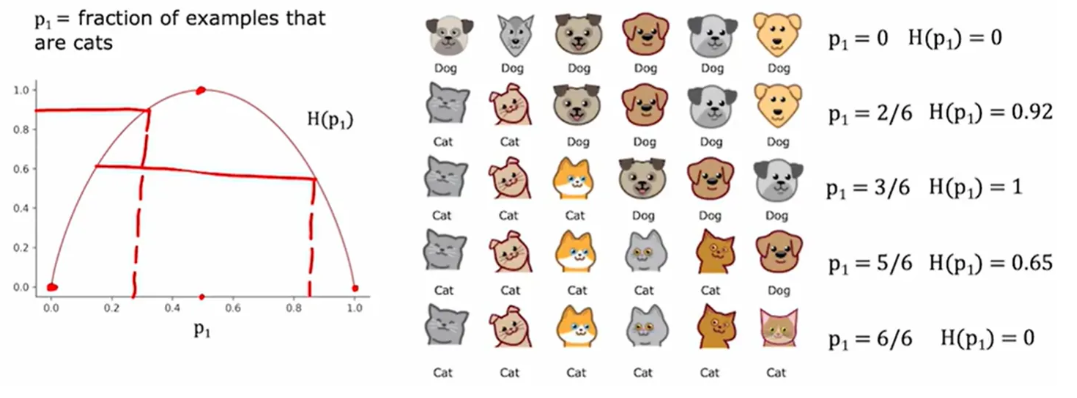
熵函数:
选择决策节点
根据熵来选决策节点,选择该结点后,使熵相对从前降低最多
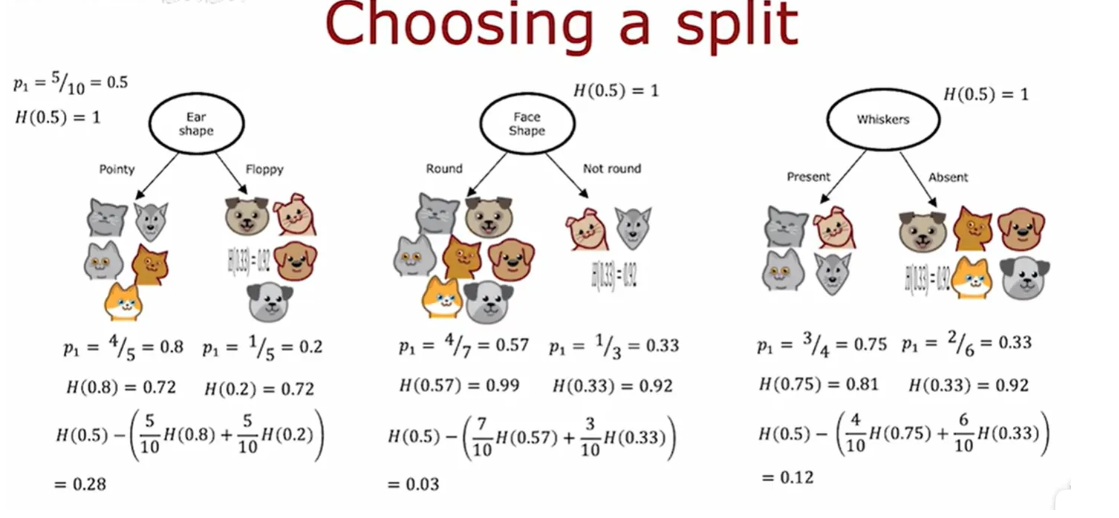
根据不同划分计算p1(猫在子集的比例),再根据熵函数算取熵,由于有两个子集,将两个熵根据
子集比例加权熵,算取新的熵,再用原来的熵减去划分后的新熵,此时得到了信息增益
信息增益

p1 left为猫占左子树的比例, w left为左子树总样本的比例,p1 root为猫占总样本的比例
解决更复杂的问题
-
解决多特征分类:独热编码 one-hot
如果一个分类特征有k种可能,就创建k个二元特征替代它
如耳朵的形状有三种,此时划分三个决策节点,是否是圆耳,是否是尖耳,是否是方耳
通过该思想,可将其转化为神经网络或逻辑回归,前五列为特征
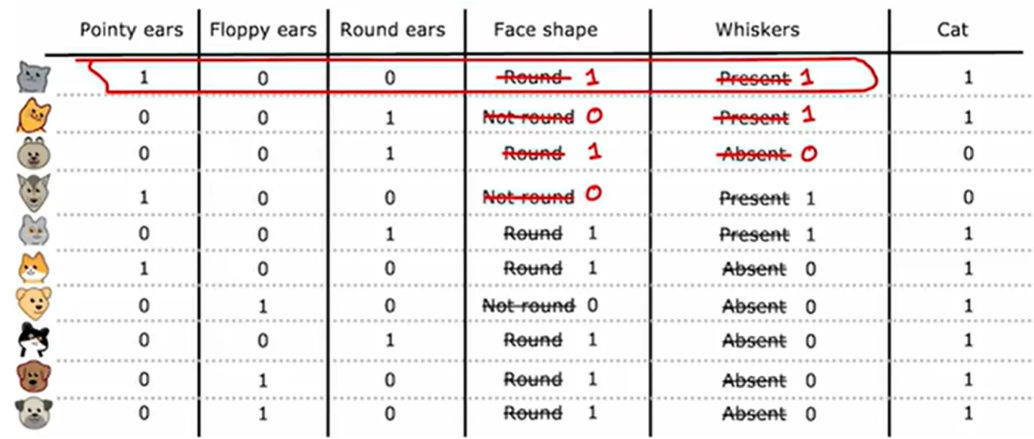
-
解决连续值特征:设置阈值
如增加体重特征,可选择最信息增益的体重划分
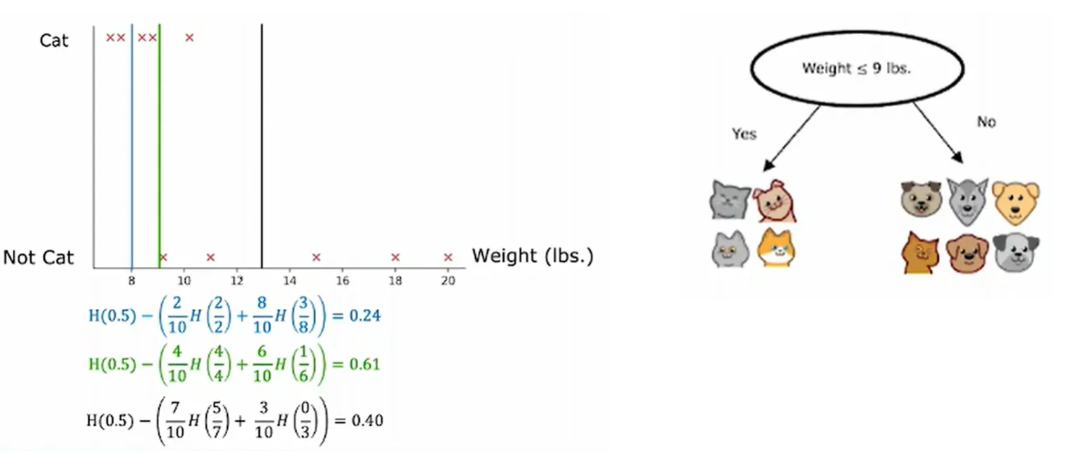
回归树
对比决策树,将熵函数部分改为方差,回归树选择方差减少最大的特征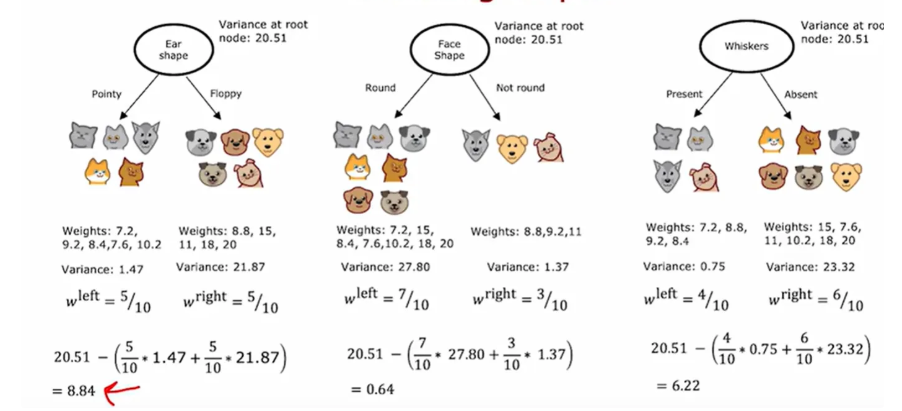
多个决策树:树集成
单个决策树可能对微小变化高度敏感,如更改一个样本就可能让决策节点发生改变,生成与以往不同的子树,使用树集成使算法不那么敏感,提高健壮性
构建树集成
给定m size的训练集,执行B次这样的操作:使用放回取样抽取m次, 生成新的数据集,并在此上训练一个决策树 (此为袋装决策树 bagging,B为生成决策树的数量)
随机森林算法 random forest
在袋装决策树基础上,选择决策节点时,若有n个特征,随机选出k个特征(k<n),并k个特征进行选择信息增益最大的特征,若n很大,则k取$\sqrt{n}$
提升决策树 boosted decision tree
给定m size的训练集,执行B次这样的操作:使用放回取样抽取m次,此处抽取的概率并不再是1/m,而是根据前面训练的决策树中错分的样本(让错分样本概率更高),得到加权数据集,并在此上训练一个决策树
即第一次循环正常使用训练集训练得到决策树,第二次循环采用放回取样,并更容易抽到第一次错分的样例….
XGBoost (eXtreme Gradient Boosting)
开源的,高效率,有默认划分终止条件的,有正则化预防过拟合的
XGBoost 为不同训练样本分配不同权重,而不是放回取样
什么时候用决策树
数据是表格类型,结构化数据适合决策树,且决策树运行更快。
神经网络在结构化和非结构化数据表现都好,不过神经网络更慢,(非结构化数据例如图像音频),
神经网络优势为可以迁徙学习,易串联神经网络,使用来构建更大的学习系统




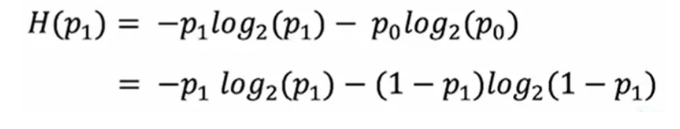
















 632
632

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








