Java蓝桥杯试题集——算法训练ALGO-3——K好数

最新推荐文章于 2022-04-04 16:11:24 发布

LimonSea

最新推荐文章于 2022-04-04 16:11:24 发布

阅读量668

点赞数

CC 4.0 BY-SA版权

分类专栏：蓝桥杯题解文章标签：蓝桥杯 Java

本文链接：https://blog.youkuaiyun.com/LimonSea/article/details/86941839

蓝桥杯题解专栏收录该内容

22 篇文章

订阅专栏

本文通过一个具体的数位DP题目，详细介绍了如何使用动态规划解决数字限制下的计数问题。文章首先解释了题目的含义，然后逐步解析了解题思路，最后给出了完整的Java代码实现。理解动态规划的应用，对于解决类似问题具有很高的参考价值。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目要求

解题思路

刚开始吧，这题我读了好几遍也没读懂。。。

意思就是，如果L是2，K是4，那么就是在4进制的所有两位数中，相邻位的数字不挨着的数。

动态规划忘得差不多了，读别人的代码研究了好久。。

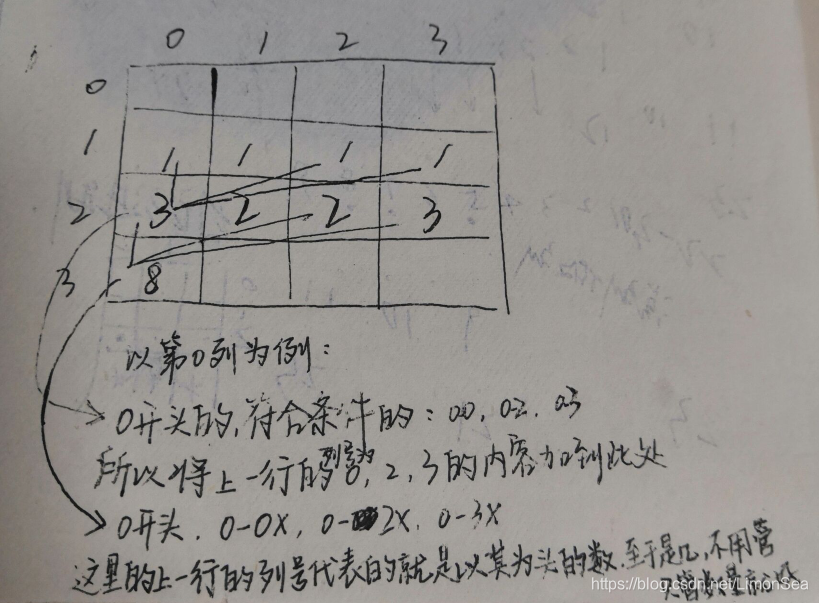
我对本题解法的理解：

首先建立一个二维数组，每行k个，代表着k进制；行号，代表位数，求L位数的最终结果，就将L行除了第0列的所有数加起来。

列号，代表每次循环时以它打头的数，每次只要判断 j 能不能放在 m 前面即可。

dp [ i ] [ j ]存的是当 i 位数时，j 打头的符合条件的数的数量。

import java.util.Scanner;

public class Main {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		Scanner in = new Scanner(System.in);
		int k = in.nextInt();
		int l = in.nextInt();
		int[][] dp = new int[101][101];
		int mod = 1000000007;
		
		for (int i = 0; i < k; i++) {	// 一位数的时候都符合
			dp[1][i] = 1;
		}
		
		for (int i = 2; i <= l; i++) {	// i是位数
			for (int j = 0; j < k; j++) {	// j表示i位数的第一位，比如：10，100，1000中的1
				for (int m = 0; m < k; m++) {
					if (m != j - 1 && m != j + 1) {	// m可以看成是下一行要往j后面放的数，和j进行比较
						dp[i][j] += dp[i-1][m];
						dp[i][j] %= mod;
					}
				}
			}
		}
		int sum = 0;
		// 求l行的和，就是最终答案，第一位不能是0
		for (int i = 1; i < k; i++) {
			sum += dp[l][i];
			sum %= mod;
		}
		System.out.println(sum);
		
		in.close();
	}

}