poj 3926 Parade 题解（单调队列优化DP）

原题链接：
poj

题意简述

你有一个城市，形状是一个类似$n\ast m$的方格纸。（画张图后）很明显，有$(n+1)\ast m$条横着的路径。给定每条路径的长度，人民对皇帝的评分（有负）。给定一个$k$，表示皇帝在横向走的时候，路径长度不能超过$k$。竖着走没有任何权值，也不会有任何限制，但是只能往上（北面）走。然后皇帝从最下面开始，要在最上面的某一个点停止。求经过路径上评分的和的最大值。

（样例图片）

数据

输入格式

多组数据，0 0 0结束。对于每组：

n m k//rt,n<=100,m<=10000,k<=3000000
val val ... val
val val ... val
... 
val val ... val
//n+1行,m列
#珂能有负！！！
//表示每条横路上人民对皇帝的评分
len len ... len
len len ... len
...
len len ... len
//n+1行,m列
#没有负的！！！
//表示每条横路的长度

输出格式

对于每组数据，

ans
//一行，表示答案

样例

输入
2 3 2
7 8 1
4 5 6
1 2 3
1 1 1
1 1 1
1 1 1
0 0 0
输出
27

思路

其实，由于我们是从最下面开始，那么我们把读入的矩阵的行反一下，也会更好写。

对于所有的下文，请将矩阵的行反过来理解下面的话

正文。
很明显，这个题是要$dp$的。$dp[i][j]$表示从最上面（反过来之后的上面，就是原来的下面，第一次提醒，以后就不说了）到$(i,j)$位置的边的评分最大值，并且保证横向差值$<=k$。

那么，我们就要从上一行的某个$(i-1,kk)$转移到现在的$(i,j)$。这个转移的答案是$dp[i-1][kk]+区间评分值和$，条件是$区间长度和<=k$。

Q:那个$kk$是啥？
A:为了不和题目里面给的$k$重名，叫$kk$（坤坤）。不过后面被优化掉了，所以代码里面没有。

维护前缀和后，设$val[i][j]$表示第$i$行$[1,j]$区间内的评分值和，$len[i][j]$表示第$i$行$[1,j]$区间内的长度和。然后我们就要讨论$k$是$<j$的还是$>=j$的，然后：

1. $k<=j$。此时 d p [ i ] [ j ] = m a x { d p [ i − 1 ] [ k k ] + v a l [ i ] [ j ] − v a l [ i ] [ k k ] } dp[i][j]=max\{dp[i-1][kk]+val[i][j]-val[i][kk]\} dp[i][j]=max{dp[i−1][kk]+val[i][j]−val[i][kk]}。

   Q:为啥后面那个$len[i][kk]$的$kk$没有减$1$。。。说好的区间和呢。。。
   A:我来仔♂细讲讲。看图：
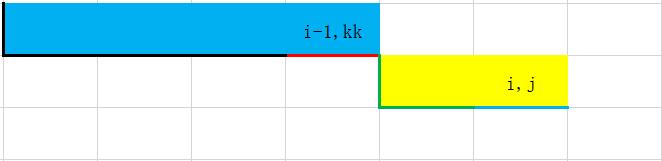   假设矩阵是这样的（请区分实心矩阵和边框）。蓝色边框表示$(i,j)$，红色边框表示$(i-1,kk)$。然后此时$dp[i][j]$多于$dp[i-1][kk]$的部分就是黄色矩阵部分的下面的边框（一条绿色的+一条蓝色的）。我们发现这个部分是不包括$kk$的，所以我们是$val[i][j]-val[i][kk]$，而不用在$kk$后面加上一个$-1$（如果加上了的话，就会把$kk$这条边算重。这是不允许的。）

  此时如何优化呢？我们发现，这个$val[i][j]$是不会变的呢，然后只要保证
  $dp[i-1][kk]-val[i][kk]$最大就珂以了鸭。然后如何保证这个最大呢？我们丢进单调
  队列即珂。然后要注意每次要弄掉那些过时的状态。什么状态过时了呢？如果我
  们在枚举$j$的时候，有一个$kk$满足$len[i][j]-len[i][kk]>k$，那么因为边长都是
  正的，$len[i][j]$会越来越大，那么$len[i][j]-len[i][kk]$就会一直大于$k$，也就不
  会有用了。我们踢掉它即珂。

2. k>=j
   此时方程变为 d p [ i ] [ j ] = m a x { d p [ i − 1 ] [ k k ] + v a l [ i ] [ k k ] − v a l [ i ] [ j ] } dp[i][j]=max\{dp[i-1][kk]+val[i][kk]-val[i][j]\} dp[i][j]=max{dp[i−1][kk]+val[i][kk]−val[i][j]}。此时我们要把$dp[i-1][kk]+val[i][kk]$丢进单调队列。注意此时$j$的枚举顺序也要变，因为此时条件是$len[kk]-len[j]<k$，随着$j$的减小，$len[kk]-len[j]$才会不断变大。所以$j$要倒着枚举。别的都差不多。

（注意到一个小问题，$kk=j$的情况被算了两次，不过也就是$O(1)$，不影响时间复杂度。）

代码:

#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;
namespace Flandle_Scarlet
{
    #define N 110
    #define M 10100
    #define CLS(x) memset(x,0,sizeof(x))
    #define MEM(x,a) memset(x,a,sizeof(x))
    int val[N][M];
    int len[N][M];//prefix sum
    int n,m,k;
    void R1(int &x)
    {
        x=0;char c=getchar();int f=1;
        while(c<'0' or c>'9') f=(c=='-')?-1:1,c=getchar();
        while(c>='0' and c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar();
        x=(f==1)?x:-x;
    }
    void Input()
    {
        for(int i=n+1;i>=1;--i)//反向读入
        {
            for(int j=1;j<=m;++j)
            {
                R1(val[i][j]);
                val[i][j]+=val[i][j-1];//直接维护前缀和（也就是说，原本的那个val数组我不要了，只保留前缀和数组。这样省空间。下同。）
            }
        }
        for(int i=n+1;i>=1;--i)//反向读入
        {
            for(int j=1;j<=m;++j)
            {
                R1(len[i][j]);
                len[i][j]+=len[i][j-1];//直接维护前缀和
            }
        }
    }

    int dp[N][M];
    struct node
    {
        int pos,val;
        //pos:kk的位置
        //val:此时的答案(的一部分,就是丢进单调队列的那一部分)
    }Q[M];int head,tail;
    void Soviet()
    {
        for(int i=1;i<=n+1;++i)
        {
            head=0,tail=0;
            for(int j=0;j<=m;++j)//正向枚举kk<j的情况(更准确的说，是kk<=j的情况)
            {
                int tmp=dp[i-1][j]-val[i][j];//这个就是要丢进单调队列的部分
                while(head<tail and Q[tail-1].val<=tmp) --tail;
                Q[tail++]=(node){j,tmp};//丢进单调队列

                while(head<tail and len[i][j]-len[i][Q[head].pos]>k) ++head;//清除过时的状态
                dp[i][j]=max(dp[i][j],Q[head].val+val[i][j]);
                //Q[head].val是满足dp[i-1][kk]-val[i][kk]最大
                //然后再加上val[i][j]才是正确的转移方程：
                //dp[i][j]=max{dp[i-1][kk]+val[i][j]-val[i][kk]}
            }

            head=0,tail=0;
            for(int j=m;j>=0;--j)//反向枚举kk>=j的情况
            {
                int tmp=dp[i-1][j]+val[i][j];
                while(head<tail and Q[tail-1].val<=tmp) --tail;
                Q[tail++]=(node){j,tmp};

                while(head<tail and len[i][Q[head].pos]-len[i][j]>k) ++head;//清除过时的状态
                
                dp[i][j]=max(dp[i][j],Q[head].val-val[i][j]);
                //Q[head].val是满足dp[i-1][kk]+val[i][kk]最大
                //再减去val[i][j]才是正确的方程：
                //dp[i][j]=max{dp[i-1][kk]+val[i][kk]-val[i][j]}
            }
        }
        int ans=0xcfcfcfcf;
        for(int i=0;i<=m;++i)
        {
            ans=max(ans,dp[n+1][i]);
        }
        printf("%d\n",ans);
    }

    void InitAll()
    {
        MEM(dp,0xcf);
        CLS(dp[0]);
        CLS(val);
        CLS(len);
        head=tail=0;
    }
    void IsMyWife()
    {
        if (0)
        {
            freopen("","r",stdin);
            freopen("","w",stdout);
        }
        while(~scanf("%d%d%d",&n,&m,&k) and n+m+k)
        //注意：是and n+m+k
        //不是and n and m and k
        //偷偷说一句,and就是&&运算符
        {
            InitAll();
            Input();
            Soviet();
        }
    }
};
int main()
{
    Flandle_Scarlet::IsMyWife();
    return 0;
}

回到总题解界面