1.特殊矩阵
1.1什么是特殊矩阵
特殊矩阵是假若值相同的元素或者零元素在矩阵中的分布有一定规律,则我们称此类矩阵为特殊矩阵。
2.两类特殊矩阵
2.1通用性的特殊矩阵
分别有零矩阵、幺矩阵、单位矩阵,随机矩阵,标准正太分布随机矩阵,相应的MATLAB有创建上述矩阵的函数,如下表所示:
| 函数名 | 作用 |
| zeros | 产生全0矩阵,即零矩阵 |
| ones | 产生全1矩阵,即幺矩阵 |
| eye | 产生对角线为1的矩阵,当矩阵为方阵时,得到一个单位矩阵 |
| rand | 产生(0,1)区间均匀分布的随机矩阵 |
| randn | 产生均值为0,方差为1的标准正态分布随机矩阵 |
调用演示如下:
(1)zeros函数
<1>zeors(m):产生m x m零矩阵
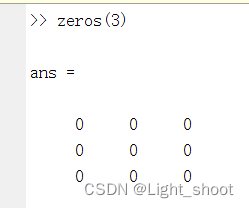
<2>zeors(m,n)产生mxn零矩阵

<3>zeors(size(A)):产生与矩阵A同等大小的零矩阵

(2)ones函数
<1>x =ones 返回标量1
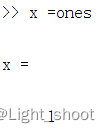
<2>ones(n):产生n x n的全1矩阵
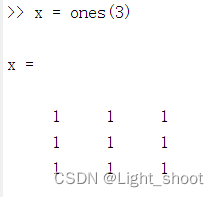
<3>ones(m,n):产生mxn的全1矩阵

<4>ones(size(A)):产生和矩阵A同等大小的全1矩阵

(3)eye函数
<1>x =eye :返回标量1

<2>eye(n):产生一个主对角线元素为 1 且其他位置元素为 0 的n x n单位矩阵

<3>eye(m,n):产生一个主对角线元素为 1 且其他位置元素为 0 的m x n单位矩阵

<4>eye(size(A)):产生一个主对角线元素为 1 且其他位置元素为 0 和矩阵A一样大小的单位矩阵

(4)rand函数
<1>x =rand:返回从区间 (0,1) 的均匀分布中得到的随机标量
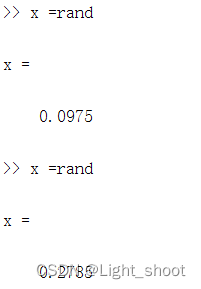
<2>rand(n):产生一个由均匀分布的随机数组成的
n×n矩阵

<3>rand(m,n): 产生一个由均匀分布的随机数组成的 m×
n矩阵

<4>rand(size(A)) : 产生一个由均匀分布的随机数组成的和矩阵A同样大小的矩阵

(5)randn函数
<1> x =randn:返回一个从标准正态分布中得到的随机标量

<2>randn(n): 产生一个由正太分布的随机数组成的
n×n矩阵

<3>randn(m,n):产生一个由正太分布的随机数组成的 m×
n矩阵
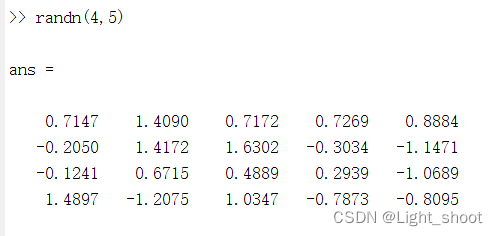
<4>randn(size(A)):产生一个由正太分布的随机数组成的和矩阵A一样大小的矩阵

2.2用于专门学科的特殊矩阵
分别有幻方矩阵、范德蒙矩阵、希尔伯特矩阵、伴随矩阵、帕斯卡矩阵,MATLAB相应创建上述矩阵的函数如下表:
| 函数名 | 作用 |
| magic | 生成幻方矩阵 |
| vander | 生成范德蒙矩阵 |
| hilb | 生成希尔伯特矩阵 |
| compan | 生成伴随矩阵 |
| pascal | 生成帕斯卡矩阵 |
2.2.1魔方矩阵
定义:
魔方矩阵又称幻方,是有相同的行数和列数,并在每行每列、对角线上的和都相等的矩阵。魔方矩阵中的每个元素不能相同。你能构造任何大小(除了2x2)的魔方矩阵。
特点:
- n阶魔方阵由1,2,3,......,n^2,共n^2个整数组成,且每行、每列以及主、副对角线上各n个元素之和都相等
- n阶魔方阵每行每列元素的和为(1+2+3+.......+n^2)/n = (n+n^3)/2
- n>2时有很多不同的魔方阵,MATLAB函数magic(n)产生一个特定的魔方矩阵。
语法:
M = magic( n ):返回由 1 到 n2 的整数构成并且总行数和总列数相等的 n×n 矩阵。n 的阶数必须是大于或等于 3 的标量才能创建有效的幻方矩阵。
演示:

2.2.2范德蒙矩阵
定义:

语法:
A = vander(v):返回 Vandermonde 矩阵 以使其列是向量 v 的幂。
演示:

2.2.3希伯特矩阵
定义:
希尔伯特矩阵(Hilbert matrix)是一种数学变换矩阵,正定,且高度病态(即,任何一个元素发生一点变动,整个矩阵的值和逆矩阵都会发生巨大变化),病态程度和阶数相关。

语法:
H = hilb(n): 返回阶数为 n 的 Hilbert 矩阵,Hilbert 矩阵的元素由 H(i,j) = 1/(i + j – 1) 指定。
演示:

2.2.4伴随矩阵
定义:
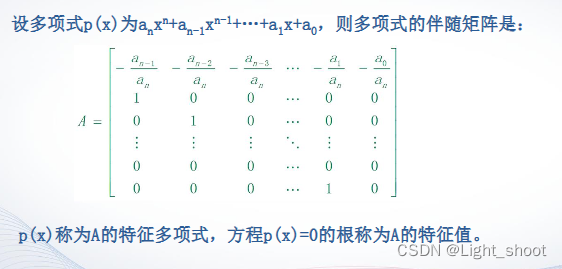

语法:
A = compan(u) 返回第一行为 -u(2:n)/u(1) 的对应伴随矩阵,其中 u 是多项式系数向量。compan(u) 的特征值是多项式的根。
演示:

2.2.5帕斯卡矩阵
定义:
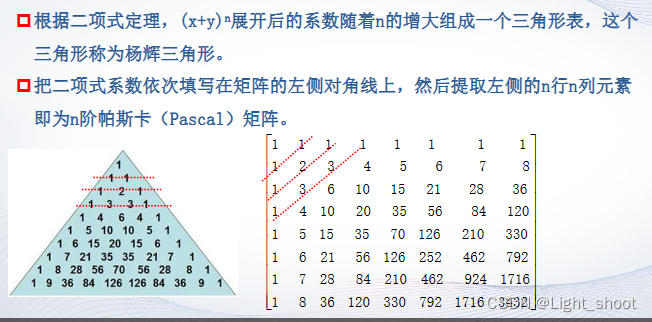
特点:

语法:

演示:






 文章介绍了MATLAB中用于创建特殊矩阵的函数,包括零矩阵、幺矩阵、单位矩阵、随机矩阵和标准正态分布随机矩阵的生成方法。此外,还详细阐述了幻方矩阵、范德蒙矩阵、希尔伯特矩阵、伴随矩阵和帕斯卡矩阵的定义、特点及MATLAB生成这些矩阵的函数用法。
文章介绍了MATLAB中用于创建特殊矩阵的函数,包括零矩阵、幺矩阵、单位矩阵、随机矩阵和标准正态分布随机矩阵的生成方法。此外,还详细阐述了幻方矩阵、范德蒙矩阵、希尔伯特矩阵、伴随矩阵和帕斯卡矩阵的定义、特点及MATLAB生成这些矩阵的函数用法。
















 2877
2877

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








