MATLAB矩阵变换

目录

1.对角阵

1.1类别

1.2提取矩阵的对角线元素

1.2.1代码演示

 1.3构造对角矩阵

1.3.1代码演示

2.三角矩阵

2.1类别

2.2提取三角矩阵元素

2.2.1代码演示

3.矩阵的转置

3.1运算符

3.2代码演示

4.矩阵的旋转

4.1代码演示

5.矩阵的翻转

5.1定义

5.2实现函数

5.3代码演示

6. 矩阵的求逆

6.1概念

6.2实现函数

6.2.1代码演示

6.2.2 例子

---

1.对角阵

1.1类别

1. 对角阵：只有对角线上有非零元素的矩阵
2. 数量矩阵：对角线上的元素相等的对角矩阵
3. 单位矩阵：对角线上的元素都为1的对角矩阵。

---

1.2提取矩阵的对角线元素

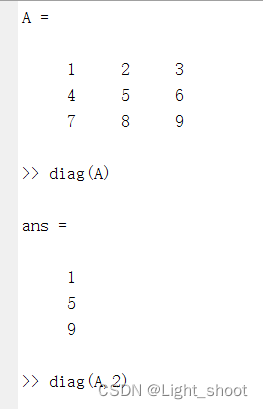
1. diag（A）：提取矩阵A主对角线元素，产生一个列向量
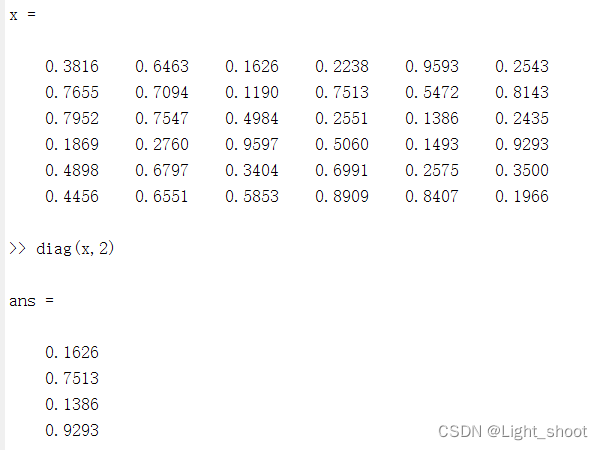
2. diag（A，K）：提取矩阵A第K条对角线的元素，产生一个列向量

1.2.1代码演示

 

---

 1.3构造对角矩阵

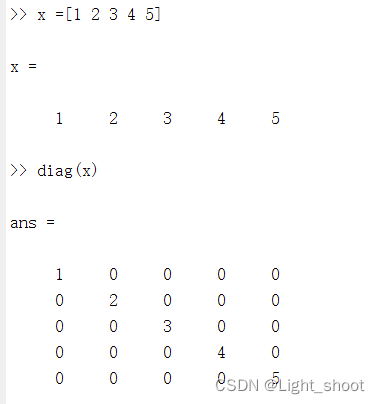
1. diag（V）：以向量V为主对角线元素，产生对角矩阵
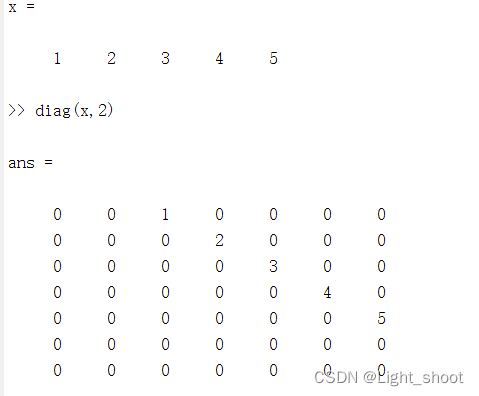
2. diag（V，k）：以向量V为第K条对角线元素，产生对角矩阵

1.3.1代码演示

 

---

2.三角矩阵

2.1类别

1. 上三角阵：矩阵的对角线以下的元素全为零的矩阵
2. 下三角矩阵：对角线以上的元素全为零的矩阵

2.2提取三角矩阵元素

（1）上三角矩阵

1. triu（A）：提取矩阵A的主对角线及以上的元素
2. triu（A，k）：提取矩阵A的第k条对角线及以上的元素

（2）下三角矩阵

提取函数为tril，用法与triu函数相同，不做赘述。

2.2.1代码演示

 

---

3.矩阵的转置

3.1运算符

1. 转置运算符是小数点后面接单引号（.'）
2. 共轭转置的运算符是单引号(')，在转置得基础上还要去每个数得复共轭

3.2代码演示

---

4.矩阵的旋转

rot90（A，k）：将矩阵A逆时针方向旋转90°得k倍，当k为1时可以省略

4.1代码演示

---

5.矩阵的翻转

5.1定义

对矩阵实施左右翻转是将原矩阵得第一列和最后一列调换，第二列和倒数第二列调换，直到所有被调换。

5.2实现函数

1. fliplr（A）：对矩阵A实施左右翻转
2. flipud（A）：对矩阵A实施上下翻转

5.3代码演示

 

6. 矩阵的求逆

6.1概念

对于一个方阵A，如果存在一个与其同阶方阵B，使得AB = BA = I（I为单位矩阵），则称B为A的逆矩阵，当然，A也是B的逆矩阵。

6.2实现函数

·inv（A）：求方阵A的逆矩阵

6.2.1代码演示

6.2.2 例子